その昔とある「帝國大学」に伝説的な大先生がおられた。この先生、研究は熱心なのだが、学生の試験の採点というのにはどうも意義を感じられなかった。だからその「採点」方法は、豪快かつ超「省力化」されたものだった。学生の答案用紙の束を抱えた先生は研究室近くの階段の中ほどで立ち止まると、やにわに答案を投げ上げた。ひらひらとしばらく宙を舞ったあと、当然ながら答案用紙は階段の上に散らばる。先生は最も上の段に落ちた答案に100と朱で書き、次の段の答案をまとめるとそれらすべてに90と書き、・・・一番下の答案は0。これで「採点」は終わった。
まあ今やれば、採点偽装だとマスコミが書き立てるだろうが、古き良き時代の話である。この宝くじ的な「採点」を非難されることもなく、この「階段教授」は定年を全うされたと聞く。学生が一生懸命書いた答案を、とお怒りの方はこの「合理性」をよく考えていただきたい。「階段教授」には再度ご登場願う。
このエピソードを思い出したのは、公立中学で先生が生徒の点数を偽造したというニュースを聞いたとき。藤沢市で<昨年12月、2年生の理科を担当する男性教諭(39)が、後期中間試験の採点を期日内に行わず、生徒や保護者に点数を通知する「成績カード」にでたらめな点数を記載していた>(読売1月21日)。
この教諭、<「部活動が忙しかった」として採点に取りかからず、2年生161人全員の点数を過去の試験結果などから推測し、9日に成績カードにパソコンで入力、12日に生徒に配布した。>という。もちろん帰ってきた答案用紙の点数と「成績カード」の点数が違うので発覚したというお粗末。
このニュース、二日間に渡って各紙各局とも取り上げた。確かに点数の「偽装」は褒められたことではないし教育上よろしくない。ただ、耐震強度偽装や米牛肉偽装(前者は骨抜き、後者は骨抜かずの犯罪だ)のような命にかかわることではない。これほど大きく取り上げられるのが不思議だ。答案が返却されるテストであるから、そうでない例えば入試などの偽装と違い、バレるまでの時間稼ぎをやったに過ぎない。
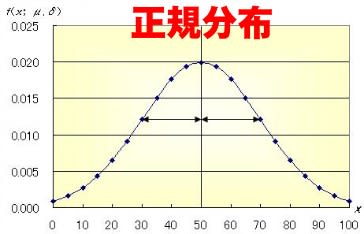
「階段教授」と「”部活動命”先生」の違いは何だろう。「罪」としては「階段教授」の方が重いと思うが、「採点」の方法は「階段教授」の方がはるかに”優れて”いる。それは、「採点」が迅速ということもあるが、もっと本質的な問題、つまり得点の分布が、「教授」の方は”実際”に近い「正規分布」(冒頭のグラフのような)を示すはずだが、「先生」のように「過去の試験結果などから推測」して人為的に点数を決めた場合は、「分布」に非常な偏りが現れる。だから照合することなしにその分布だけを見て簡単に偽装を見破られてしまう。あるいは「採点」結果がトータルとして非現実的とも言える。
小生としては、むしろこの「理科の先生」の、統計学の初歩も忘れ去っている?その「学力」が心配だ。クラブ活動ばかりに熱中しすぎているのでないかと。
◆正規分布と偏差値ー計算方法のおさらい
同一集団での身長や体重の分布、また平等な社会での所得の分布、50m走りの記録、学校のテストの成績などは、経験的に上に掲げたような分布、つまり「正規分布」になると言われてきた。だいたい「平均値」の周りに「人」が密集する。山の一番高いところの付近にいることで、多くの人が「自分は人並み」という安心感を得る。いわば日本人好みが「正規分布」なのだ。
統計学でも一番基本的な分布であるこの「正規分布」の理論をいわゆる進路指導に活用したものが、日本人なら誰でも知っている「偏差値」だ。実はこの「偏差値」は日本独自のもので、東京都港区の中学校教諭であった桑田昭三先生が、1957年に進路指導を数値を使って正確にやるために開発したものだ。
ちょうど平均点なら偏差値は50になり、科目ごとの平均点の違いなどが隠れて自分の相対的な順位が容易につかめるというメリットがあったため、この偏差値は全国の学校に拡がり、特に1965年に旺文社がコンピューターで計算した「偏差値による大学ランキング」を公表したことから瞬く間に認知された。以降、日本では受験と偏差値は「政治とカネ」のように堅く結びつくことになった。
偏差値を計算するにはまずすべての得点のデーターから標準偏差σという値を計算する。σは直感的に言えば得点の「散らばり具合」を表す指標である。国語のように点数の散らばりの少ない科目ではこれが小さく、数学のような科目では大きくなりがちである。昨年の「大学入試センター」の結果では数学Iでσ=24.02, 国語Iでσ=17.65(100点満点換算)である。
全体の平均点をμとすると、ある人の偏差値は次の式で計算される。偏差値=(その人の得点-μ)×10÷σ+50 例えば上のセンター試験の「数学I」では平均μが51.86点と公表されている(科目ごとのμとσはセンターから必ず公表される)ので、例えば 90点を取った人の偏差値=(90-51.86)×10÷24.02+50。つまり65.88。0点でも、28.41。100点でも70.04だから、100点満点のテストの点数よりも数字的には「幅」が小さくなる。平均点が同じでも、σが違うと偏差値は異なる。例えば上の「国語I」が偶然「数学I」と平均点が同じであったとしても、90点の人の偏差値は71.61になる。つまり国語の方が同じ90点でも「成績が良い」ことを意味している。
この偏差値の計算法で分かるように、偏差値を絶対的な比較に使うことはできない。つまり「オレ得点55点、お前50点。オレの方が1割成績がいい」は正しいが、この得点を偏差値に置き換えて議論してもも意味がない。これは同じ考えで数値化している「知能指数」(たぶん桑田先生はこの計算方法を参考にしたのだ)についても同じことが言える。「偏差値」が平均を50としているように、「知能指数」では平均を100としている。だから「オレ知能指数150,お前100。オレの方が50%頭いい」という人の知能は高くないと言うか、全く数値の意味を誤解している(そもそも「50%頭いい」という比較が無意味だが)。
「偏差値」から得られる数値的な情報は、実は自分の「順位」、つまり「分布」のどのあたりにいるかということだけなのだ。そしてその大前提には成績の分布が「正規分布」であることが仮定されている。つまり実際には試験によって、成績が二極化した「らくだのこぶ」型の分布になることがある。この場合にも、「偏差値」はもちろん計算できるが、「順位」はデタラメになり、つまり「偏差値」を基にした「進学指導」は崩壊するのである。
このことを逆にとらえて、「試験の成績が正規分布をしているからいい問題だった」と主張する先生がある。大学入試センターの問題の「適切さ」を「証明」するのに、成績分布が美しく正規分布をしているグラフを示されたこともある。「階段教授」の「採点」が「合理的」と言ったのは、恐らくこの分布が「正規分布」になったであろうからだ。しかし「適切」とは言えないだろう。
◆「正規分布」社会にサヨナラ-勝ち組/負け組の「ラクダ分布」社会へ
日本の「進学指導」に神のように君臨し、いわば「神学指導」の域にまで高めた偏差値だが、その賞味期限は終わりを迎えつつある。第一の大きな理由はもちろん少子化だ。これまでのように大学や高校が受験者を選ぶ時代にこそ、「偏差値」による生徒の”輪切り”は有効だったが、生徒の方が学校を選ぶ少子化の時代には笑止千万なただの数字だ。
しかしもっと大きな理由は日本が急速に<「正規分布」社会>でなくなりつつあることだ。日本は長い間「同質社会」であると言われてきた。同じ程度の収入、同じような価値観、つまり「平均的」な人が圧倒的多数を占めるという、正規分布のグラフで言うと、平均μの周りに押し合い圧し合いしている、標準偏差σの小さい社会。当然子供たちの成績の分布も典型的正規分布になり、「どんぐりの背比べ」なので競争も激しかった。選択肢の少ない社会と言えるが、周りを見渡して、「まあ人並み」と正規分布の”山”の中心にいることで安心感を得ていた安定的な社会でもある。
しかしいわゆる「小泉-竹中改革」路線は、日本社会を「勝ち組」と「負け組」に積極的に分化させ、正規分布から、「らくだのこぶ」分布社会へと変えようとしている。所得で言えば、平均値μの周りにはほとんど人がいなくて、大部分の人はそれよりもはるかに貧しい。それは「六本木ヒルズ族」のような人達がμを「右側」に移動させているためだが、圧倒的多数にとってはμさえ高根の花という明治以降の日本人が知らない社会になろうとしている。「平民社会」から「貴族社会」への移行と言ってもいい。
親の収入格差は子供の学力格差に直結する。もはや全国学力テストでは成績が「正規分布」することなどあり得なくなるだろう。「正規分布」を前提にしてきた「偏差値」はその意味を失う。「勝ち組」の子弟は「勝ち組」学校に”自動的”に進むので、進学競争はなくなるだろう。現在の憲法が続く限り、法の下の平等は継続されるが、「身分」の違いは歴然として、例えばイギリスのような階級社会になっていくのだろう。
そう考えると例の「階段教授」が許容されていたわけも分かる。戦前の「帝国大学」は貧しいが前途有為な子弟を”国策を担う”人材として吸収するための装置だった。その中での”民主的な”「採点」は許容の範囲内である。しかし身分社会(日本では政治の世界はすでにそうなっている)においては、自動的に「正規分布」となるような”急進的な”採点方法は御法度である。「階段教授」は今後は「シュギ者」と見なされ、、突然検察の家宅捜索を受け、ワイドショーで叩かれて、国会喚問に呼び出されるような罰を受けるに違いない。そうだ、あの時の点数は風任せだったが、これからの日本では点数もカネ任せになっていくのだ。
まあ今やれば、採点偽装だとマスコミが書き立てるだろうが、古き良き時代の話である。この宝くじ的な「採点」を非難されることもなく、この「階段教授」は定年を全うされたと聞く。学生が一生懸命書いた答案を、とお怒りの方はこの「合理性」をよく考えていただきたい。「階段教授」には再度ご登場願う。
このエピソードを思い出したのは、公立中学で先生が生徒の点数を偽造したというニュースを聞いたとき。藤沢市で<昨年12月、2年生の理科を担当する男性教諭(39)が、後期中間試験の採点を期日内に行わず、生徒や保護者に点数を通知する「成績カード」にでたらめな点数を記載していた>(読売1月21日)。
この教諭、<「部活動が忙しかった」として採点に取りかからず、2年生161人全員の点数を過去の試験結果などから推測し、9日に成績カードにパソコンで入力、12日に生徒に配布した。>という。もちろん帰ってきた答案用紙の点数と「成績カード」の点数が違うので発覚したというお粗末。
このニュース、二日間に渡って各紙各局とも取り上げた。確かに点数の「偽装」は褒められたことではないし教育上よろしくない。ただ、耐震強度偽装や米牛肉偽装(前者は骨抜き、後者は骨抜かずの犯罪だ)のような命にかかわることではない。これほど大きく取り上げられるのが不思議だ。答案が返却されるテストであるから、そうでない例えば入試などの偽装と違い、バレるまでの時間稼ぎをやったに過ぎない。
「階段教授」と「”部活動命”先生」の違いは何だろう。「罪」としては「階段教授」の方が重いと思うが、「採点」の方法は「階段教授」の方がはるかに”優れて”いる。それは、「採点」が迅速ということもあるが、もっと本質的な問題、つまり得点の分布が、「教授」の方は”実際”に近い「正規分布」(冒頭のグラフのような)を示すはずだが、「先生」のように「過去の試験結果などから推測」して人為的に点数を決めた場合は、「分布」に非常な偏りが現れる。だから照合することなしにその分布だけを見て簡単に偽装を見破られてしまう。あるいは「採点」結果がトータルとして非現実的とも言える。
小生としては、むしろこの「理科の先生」の、統計学の初歩も忘れ去っている?その「学力」が心配だ。クラブ活動ばかりに熱中しすぎているのでないかと。
◆正規分布と偏差値ー計算方法のおさらい
同一集団での身長や体重の分布、また平等な社会での所得の分布、50m走りの記録、学校のテストの成績などは、経験的に上に掲げたような分布、つまり「正規分布」になると言われてきた。だいたい「平均値」の周りに「人」が密集する。山の一番高いところの付近にいることで、多くの人が「自分は人並み」という安心感を得る。いわば日本人好みが「正規分布」なのだ。
統計学でも一番基本的な分布であるこの「正規分布」の理論をいわゆる進路指導に活用したものが、日本人なら誰でも知っている「偏差値」だ。実はこの「偏差値」は日本独自のもので、東京都港区の中学校教諭であった桑田昭三先生が、1957年に進路指導を数値を使って正確にやるために開発したものだ。
ちょうど平均点なら偏差値は50になり、科目ごとの平均点の違いなどが隠れて自分の相対的な順位が容易につかめるというメリットがあったため、この偏差値は全国の学校に拡がり、特に1965年に旺文社がコンピューターで計算した「偏差値による大学ランキング」を公表したことから瞬く間に認知された。以降、日本では受験と偏差値は「政治とカネ」のように堅く結びつくことになった。
偏差値を計算するにはまずすべての得点のデーターから標準偏差σという値を計算する。σは直感的に言えば得点の「散らばり具合」を表す指標である。国語のように点数の散らばりの少ない科目ではこれが小さく、数学のような科目では大きくなりがちである。昨年の「大学入試センター」の結果では数学Iでσ=24.02, 国語Iでσ=17.65(100点満点換算)である。
全体の平均点をμとすると、ある人の偏差値は次の式で計算される。偏差値=(その人の得点-μ)×10÷σ+50 例えば上のセンター試験の「数学I」では平均μが51.86点と公表されている(科目ごとのμとσはセンターから必ず公表される)ので、例えば 90点を取った人の偏差値=(90-51.86)×10÷24.02+50。つまり65.88。0点でも、28.41。100点でも70.04だから、100点満点のテストの点数よりも数字的には「幅」が小さくなる。平均点が同じでも、σが違うと偏差値は異なる。例えば上の「国語I」が偶然「数学I」と平均点が同じであったとしても、90点の人の偏差値は71.61になる。つまり国語の方が同じ90点でも「成績が良い」ことを意味している。
この偏差値の計算法で分かるように、偏差値を絶対的な比較に使うことはできない。つまり「オレ得点55点、お前50点。オレの方が1割成績がいい」は正しいが、この得点を偏差値に置き換えて議論してもも意味がない。これは同じ考えで数値化している「知能指数」(たぶん桑田先生はこの計算方法を参考にしたのだ)についても同じことが言える。「偏差値」が平均を50としているように、「知能指数」では平均を100としている。だから「オレ知能指数150,お前100。オレの方が50%頭いい」という人の知能は高くないと言うか、全く数値の意味を誤解している(そもそも「50%頭いい」という比較が無意味だが)。
「偏差値」から得られる数値的な情報は、実は自分の「順位」、つまり「分布」のどのあたりにいるかということだけなのだ。そしてその大前提には成績の分布が「正規分布」であることが仮定されている。つまり実際には試験によって、成績が二極化した「らくだのこぶ」型の分布になることがある。この場合にも、「偏差値」はもちろん計算できるが、「順位」はデタラメになり、つまり「偏差値」を基にした「進学指導」は崩壊するのである。
このことを逆にとらえて、「試験の成績が正規分布をしているからいい問題だった」と主張する先生がある。大学入試センターの問題の「適切さ」を「証明」するのに、成績分布が美しく正規分布をしているグラフを示されたこともある。「階段教授」の「採点」が「合理的」と言ったのは、恐らくこの分布が「正規分布」になったであろうからだ。しかし「適切」とは言えないだろう。
◆「正規分布」社会にサヨナラ-勝ち組/負け組の「ラクダ分布」社会へ
日本の「進学指導」に神のように君臨し、いわば「神学指導」の域にまで高めた偏差値だが、その賞味期限は終わりを迎えつつある。第一の大きな理由はもちろん少子化だ。これまでのように大学や高校が受験者を選ぶ時代にこそ、「偏差値」による生徒の”輪切り”は有効だったが、生徒の方が学校を選ぶ少子化の時代には笑止千万なただの数字だ。
しかしもっと大きな理由は日本が急速に<「正規分布」社会>でなくなりつつあることだ。日本は長い間「同質社会」であると言われてきた。同じ程度の収入、同じような価値観、つまり「平均的」な人が圧倒的多数を占めるという、正規分布のグラフで言うと、平均μの周りに押し合い圧し合いしている、標準偏差σの小さい社会。当然子供たちの成績の分布も典型的正規分布になり、「どんぐりの背比べ」なので競争も激しかった。選択肢の少ない社会と言えるが、周りを見渡して、「まあ人並み」と正規分布の”山”の中心にいることで安心感を得ていた安定的な社会でもある。
しかしいわゆる「小泉-竹中改革」路線は、日本社会を「勝ち組」と「負け組」に積極的に分化させ、正規分布から、「らくだのこぶ」分布社会へと変えようとしている。所得で言えば、平均値μの周りにはほとんど人がいなくて、大部分の人はそれよりもはるかに貧しい。それは「六本木ヒルズ族」のような人達がμを「右側」に移動させているためだが、圧倒的多数にとってはμさえ高根の花という明治以降の日本人が知らない社会になろうとしている。「平民社会」から「貴族社会」への移行と言ってもいい。
親の収入格差は子供の学力格差に直結する。もはや全国学力テストでは成績が「正規分布」することなどあり得なくなるだろう。「正規分布」を前提にしてきた「偏差値」はその意味を失う。「勝ち組」の子弟は「勝ち組」学校に”自動的”に進むので、進学競争はなくなるだろう。現在の憲法が続く限り、法の下の平等は継続されるが、「身分」の違いは歴然として、例えばイギリスのような階級社会になっていくのだろう。
そう考えると例の「階段教授」が許容されていたわけも分かる。戦前の「帝国大学」は貧しいが前途有為な子弟を”国策を担う”人材として吸収するための装置だった。その中での”民主的な”「採点」は許容の範囲内である。しかし身分社会(日本では政治の世界はすでにそうなっている)においては、自動的に「正規分布」となるような”急進的な”採点方法は御法度である。「階段教授」は今後は「シュギ者」と見なされ、、突然検察の家宅捜索を受け、ワイドショーで叩かれて、国会喚問に呼び出されるような罰を受けるに違いない。そうだ、あの時の点数は風任せだったが、これからの日本では点数もカネ任せになっていくのだ。