
(1) √2 (1/√2 sin x + 1/√2 cos x) =0, sin (x + π/4) = 0 ∴ x = 3π/4, 7π/4
(2) C: y = exp(-x) y'= -exp(-x)
D: y = a sin x y'= a cos x
E: y = b sin x y' = b cos x
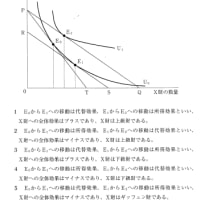
C, D は共有点Pで共通の接線 ⇔ exp(-x) = a sin x ➀, -exp(-x) = a cos x ②
➀②を辺々足して 0 = a (sin x + cos x) ∴ x = 3π/4, 7π/4
①に代入 exp(-3π/4) = 1/√2 a ∴ a = √2 exp (-3π/4), p = 3π/4
同様に exp(-7π/4) = -1/√2 b ∴ b = -√2 exp (-7π/4), q = 7π/4



















※コメント投稿者のブログIDはブログ作成者のみに通知されます