連続整数の和

問題
【問題1】
連続した2つ以上の正の整数を合計して630を作ってください。
【問題2】
問題1の解は何通りあるでしょう。

【問題2】の答え：小学生ばーじょん

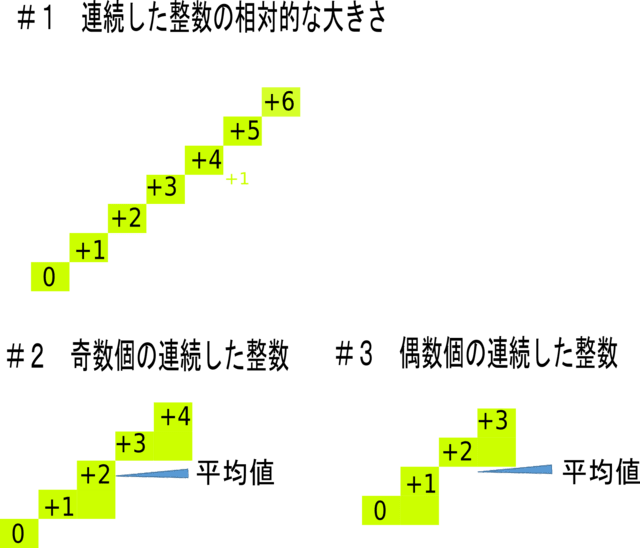
①ある整数を出発点とした連続する整数の相対的な大きさは１つずつ
　増えていきます。　図　＃１
②連続した整数の個数は奇数か偶数です。　図　＃２　図　＃３
　＜例＞4567：4個偶数、45678：5個奇数
③奇数個の場合最初の整数から真中の整数までの増分と
　真中の整数から最後の整数までの増分は同じです。
　従って真中の数字が平均値となります。
　→630が奇数の個数で割り切れれば、ある整数を起点とした
　　連続数の和は630です。
　→但し起点の整数は1またはそれよりより大きいことが条件です。
④偶数個の場合平均値は整数になりません。少数点1桁0.5で割り切れます。
　最初の整数から平均値までの増分と平均値から最後の整数までの増分は
　同じです
　→630が偶数の個数で割って小数点一桁0.5で割り切れる。
　＝1260が偶数個の個数で割り切れれば、ある整数を起点とした連続数の
　　和は630です。
　→但し起点の整数は1またはそれより大きいことが条件です。
。
　
③を満足するのは3,5,7,9,15,21,35個の7通り
④を満足するのは4,12,20,28個の4通り

計１１通りです。