前回でも取り上げたある MIP を以下の計算サーバ上で CPLEX 12.2.0.2 を用いて解いていたのだが、結局メモリ不足で終了となっていた。CPLEX 24 コアとメモリ 128Gbytes を使用しても上限と下限の差がなかなか縮まらない。少し気になる点では、Iteration 数がオーバーフローを起こしてマイナスの値になっている。
○計算サーバ(4 CPU x 6 コア = 24 コア)
CPU : AMD Opteron 8439 (2.80GHz / 6MB L3) x 4
Memory : 128GB (32 x 4GB / 800MHz)
OS : Fedora 15 for x86_64
1345804802 806509418 234.2193 8 308.0000 231.3905 1.04e+10 24.87%
There may be further error information in the clone logs.
Clique cuts applied: 19
Cover cuts applied: 259
Implied bound cuts applied: 12
Zero-half cuts applied: 11
Gomory fractional cuts applied: 10
Root node processing (before b&c):
Real time = 0.13
Parallel b&c, 24 threads:
Real time = 116783.48
Sync time (average) = 1885.41
Wait time (average) = 101.39
-------
Total (root+branch&cut) = 116783.61 sec.
Warning: MIP starts not constructed because of out-of-memory status.
Consider using CPLEX node files to reduce memory usage.
CPLEX Error 1001: Out of memory.
Solution pool: 2 solutions saved.
MIP - Error termination, integer feasible: Objective = 3.0800000000e+02
Current MIP best bound = 2.3139095673e+02 (gap = 76.609, 24.87%)
Solution time = 116785.32 sec. Iterations = -2147483648 Nodes = 1346741630 (806963365)
○計算サーバ(4 CPU x 6 コア = 24 コア)
CPU : AMD Opteron 8439 (2.80GHz / 6MB L3) x 4
Memory : 128GB (32 x 4GB / 800MHz)
OS : Fedora 15 for x86_64
1345804802 806509418 234.2193 8 308.0000 231.3905 1.04e+10 24.87%
There may be further error information in the clone logs.
Clique cuts applied: 19
Cover cuts applied: 259
Implied bound cuts applied: 12
Zero-half cuts applied: 11
Gomory fractional cuts applied: 10
Root node processing (before b&c):
Real time = 0.13
Parallel b&c, 24 threads:
Real time = 116783.48
Sync time (average) = 1885.41
Wait time (average) = 101.39
-------
Total (root+branch&cut) = 116783.61 sec.
Warning: MIP starts not constructed because of out-of-memory status.
Consider using CPLEX node files to reduce memory usage.
CPLEX Error 1001: Out of memory.
Solution pool: 2 solutions saved.
MIP - Error termination, integer feasible: Objective = 3.0800000000e+02
Current MIP best bound = 2.3139095673e+02 (gap = 76.609, 24.87%)
Solution time = 116785.32 sec. Iterations = -2147483648 Nodes = 1346741630 (806963365)













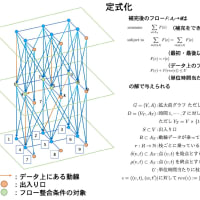


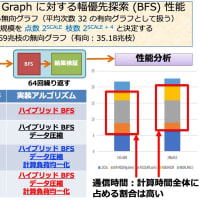
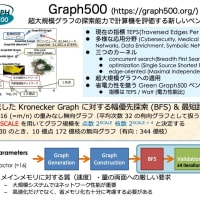

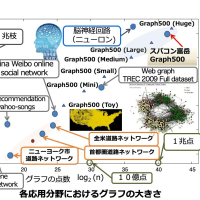





ですから、この問題を解きたいというよりも MIP ソルバーの性質(性能)を調べるのが目的です。
求められているようなページというのは,結局MIPLIB2010のページになってしまいます.人工的に作った問題というのは,極端に難しくなったり,極端に易しくなったりしますので,MIPLIB2010では現実問題から定式化されたインスタンスを集めていました.現実世界の問題を解きたいという考え方からです.ですから,どのような問題をどのように定式化して,どのくらいの変数や,どのようなタイプの制約式をどの程度含むインスタンスが,どの程度の難易度を持つ問題になり得るのかは,ある程度はMIPLIB2010のページに集約されています.また,最新の研究成果で,実際に問題を解くことに対して効果的だった論文は参照されるはずです.
定式化に関しては自由度があるので,ユーザ側の負担と考えれば,負担にはなるのですが,ユーザ側で改善の可能性はあります.解きたい問題を知っている人でないと他の定式化が可能なのかどうか判断ができないと思います.ですから,MIPソルバがもっと強力になるのを待つことにしてあきらめるか,ユーザ側で試行錯誤するかのどちらかになります.個人的には,数理計画の専門家と組んで,実際に解きたい問題に特化したノウハウを蓄積するのが良いと思います.私自身は,普通に定式化して簡単には解けなかった場合は,泥臭いのですが,試せるなら,さまざまな定式化を試して,様々なソルバでの計算の進行状況を眺めて,本当にあきらめるべきかどうかを含めて考えるしかない気がします.