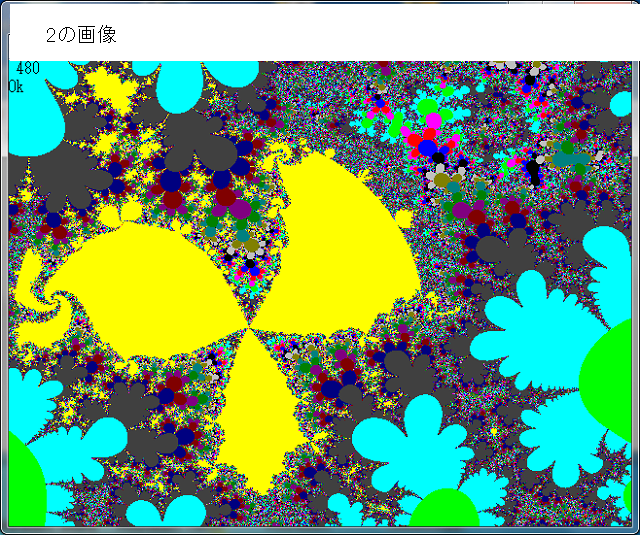
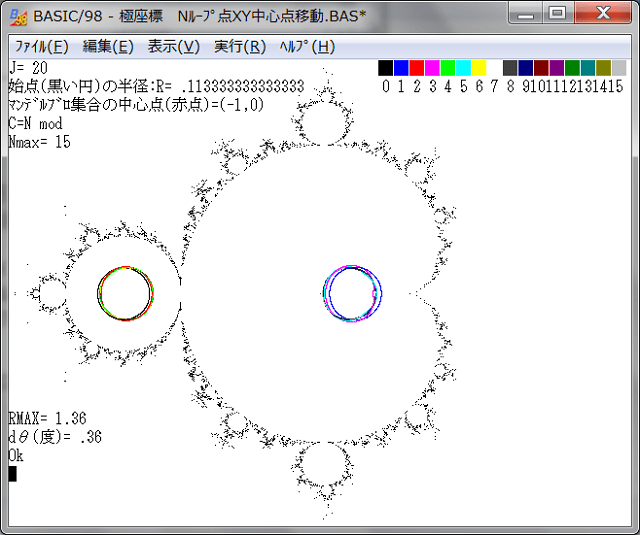
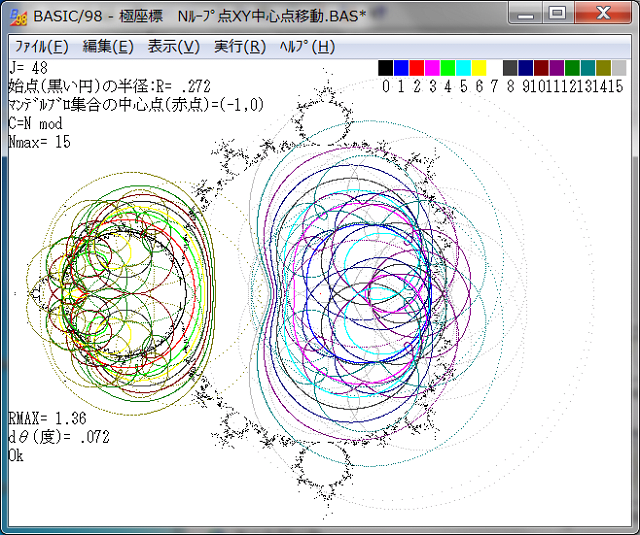
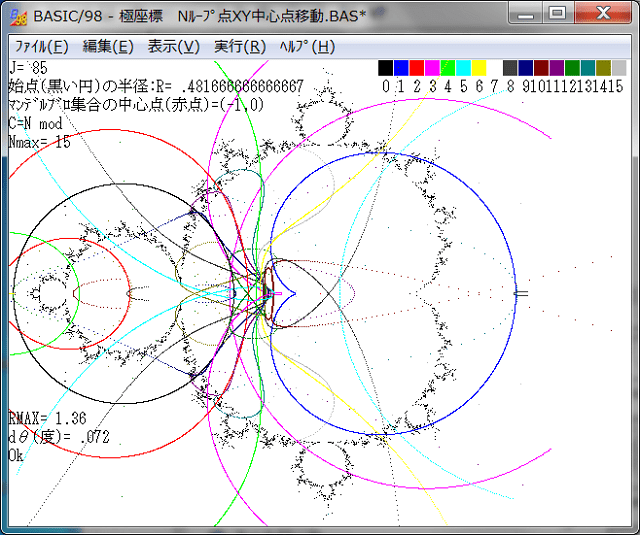
記事315では、点列:Z0,Z1,Z2,・・・,Z15の、J=10ほか各値でのθ=0→2πでの挙動(軌跡)を調べた。
今回は、J=0→240,θ=0→2π(step 0.036度)での点列の軌跡濃度を調べた。
但し、N-loop脱出条件:if X^2+Y^2>4 then next K は入れていなかった。
今回の画像は、その条件を入れてある。
今回の画像も記事315と同様に点列が同一座標となる濃度をmとすると、C=LOG(m)として色で表示する。m=0の場合は表示しない。下図がその画像である。

---------------------------------------------
参考のために、画像作成プログラムを下記しておく。
<画像データプログラム>
10 REM マンデルブロ画像1
50 CHAIN MERGE "C:\BASIC\PRO\SUBR\KOSHIKI.BAS",80,ALL
80 CHAIN MERGE "C:\BASIC\PRO\SUBR\ER1.BAS",90,ALL
90 ON ERROR GOTO 50000
91 CONSOLE ,,0,1
92 COLOR 0,7,,,2
93 CLS 3
94 GOSUB 10000
120 JMAX=240:RMAX=1.36:X0=-0.14:Y0=0:DIM Z(640,480)
122 FOR I=0 TO 640
123 FOR II=0 TO 480
124 Z(I,II)=0
125 NEXT II
126 NEXT I
130 DR=RMAX/JMAX:AA=JMAX/RMAX:NMAX=15:KMAX=1000
132 CXS=-1.5:D=1.36/320:CYS=-240*D:DTHDO=180*DTH/P
142 OPEN "C:\BASIC1\TEST\DATA.DAT" FOR OUTPUT AS #1
150 FOR J=0 TO 240
152 LOCATE 0,0:PRINT "J=";J
160 R=J*DR
162 '
172 DTH=2*P/KMAX
190 FOR K=0 TO KMAX
200 TH=K*DTH:THH=TH
210 CX=R*COS(TH)+X0
220 CY=R*SIN(TH)+Y0
221 X=0:Y=0
230 FOR N=0 TO NMAX
240 X1=X
250 X=FNR2(X,Y)+CX
260 Y=FNI2(X1,Y)+CY
270 Q=X^2+Y^2 :IF Q>4 THEN 390 ELSE 286
286 K1=INT((X-CXS)/D):J1=INT((Y-CYS)/D)
288 IF K1<0 OR J1<0 THEN 390
290 IF K1>640 OR J1>480 THEN 390
291 '
295 Z(K1,J1)=Z(K1,J1)+1
296 IF N=0 THEN PSET (K1,J1),0
300 WRITE #1,K1,J1,N
310 NEXT N
390 NEXT K
391 NEXT J
410 CLOSE #1
412 OPEN "C:\BASIC1\TEST\DATA整理.DAT" FOR OUTPUT AS #2
414 FOR KK=0 TO 640
416 FOR JJ=0 TO 480
418 WRITE #2,KK,JJ,Z(KK,JJ)
420 NEXT JJ
422 NEXT KK
500 END
-------------------------------
<画像の表示プログラム>
10 REM マンデルブロ画像1
12 CHAIN MERGE "C:\BASIC\PRO\SUBR\COLOR右上表示.BAS",20,ALL
20 CHAIN MERGE "C:\BASIC\PRO\SUBR\ARCTAN3.BAS",30,ALL
30 CHAIN MERGE "C:\BASIC\PRO\SUBR\LINE10.BAS",40,ALL
40 CHAIN MERGE "C:\BASIC\PRO\SUBR\KISEKI1.BAS",50,ALL
50 CHAIN MERGE "C:\BASIC\PRO\SUBR\KOSHIKI.BAS",60,ALL
60 CHAIN MERGE "C:\BASIC\PRO\SUBR\ZFZ.BAS",70,ALL
70 CHAIN MERGE "C:\BASIC\PRO\SUBR\FGZ.BAS",80,ALL
80 CHAIN MERGE "C:\BASIC\PRO\SUBR\ER1.BAS",90,ALL
90 ON ERROR GOTO 50000
91 CONSOLE ,,0,1
92 COLOR 0,7,,,2
93 CLS 3
94 GOSUB 10000
104 '
114 OPEN "C:\BASIC1\TEST\DATA整理.DAT" FOR INPUT AS #1
120 WHILE NOT EOF(1)
130 INPUT #1,K,J,Z
132 '
134 IF Z<=0 THEN 142
136 C=LOG(Z)
138 '
139 '
140 PSET (K,J),C
142 WEND
144 CLOSE #1
154 GOTO 199
170 LOCATE 0,0:PRINT "J=1~240 "
172 LOCATE 0,1:PRINT "C=LOG(m),C=7→C=12"
174 LOCATE 0,3:PRINT "マンデルブロ集合の中心点(赤点)=(-0.14,0)"
176 LOCATE 0,2:PRINT "但し、m=0→不表示"
183 LOCATE 0,4:PRINT "Nmax=15"
186 LOCATE 0,5:PRINT
187 LOCATE 0,6:PRINT
188 LOCATE 0,19:PRINT "RMAX=1.36"
189 LOCATE 0,20:PRINT "dθ(度)=0.072"
199 '
400 OPEN "C:\BASIC1\TEST\DATAマンデルC.DAT" FOR INPUT AS #2
402 IF EOF(2) THEN 420
404 INPUT #2,X,Y
406 PSET (X,Y),0
408 GOTO 402
410 CLOSE #2
420 GOSUB 3000
500 END