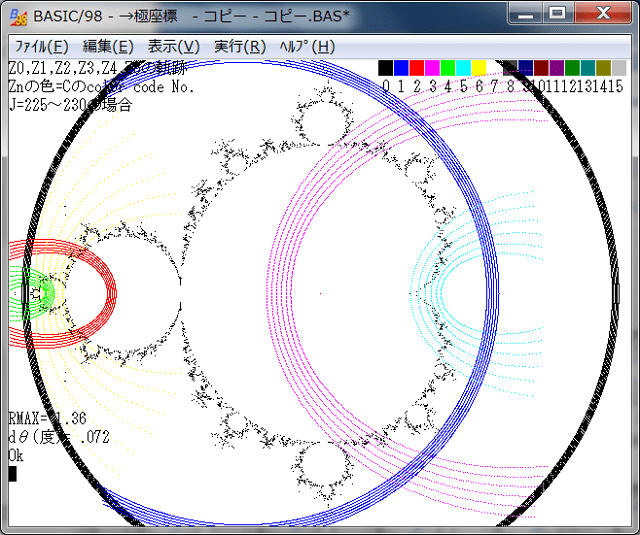
BASIC/98のcolor code は最大16色だが、code No.8以降は区別しにくい。
そこで色の区別がしやすい、0~6を使用して点列を表示する。即ち、
点列:Z0,Z1~Z45,Z46,Z47,Z48,Z49,Z50
にして、Z0→C=1(黒){注:Z0は点列の始点を表している}
Z45→C=1(青)、Z46→C=2(赤)、Z47→C=3(橙)、Z48→C=4(緑)、
Z49→C=5(青)、Z50→C=6(黄)として軌跡表示する。
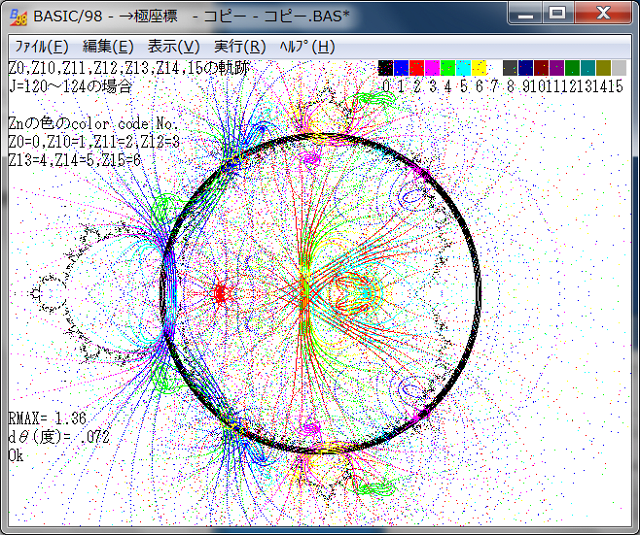
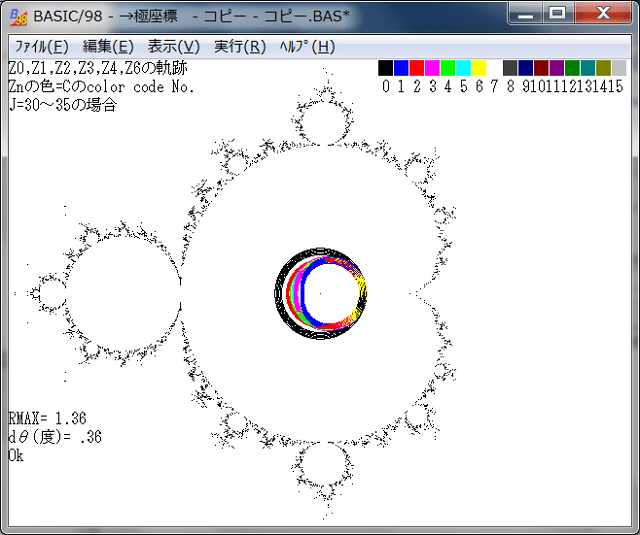
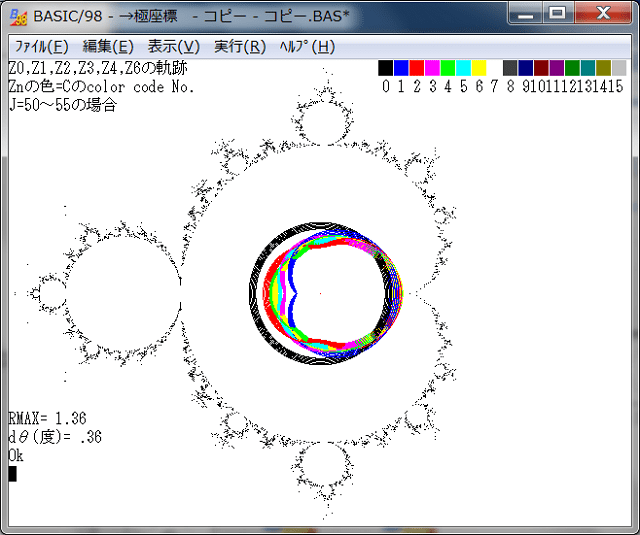
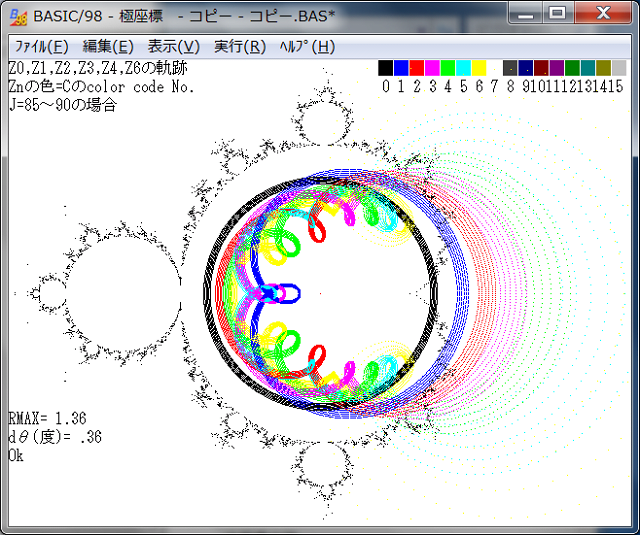
極座標の距離パラメータJを固定して、角度θ=0→2π変化させて点列の各点の軌跡を調べる。その際、Jを5ずつ連続した画像を求めると、点列の挙動が分かり易くなると同時に画像としても面白いものが得られる。以下は、その画像である。
各画像に、Jの値を示してある。
***
下図から分かるように、Znのnが大きくなると前記事で予想したように、点列の挙動は更に複雑になる。特に始点:Z0(黒い円)が、Z^2マンデルブロ集合の境界線に接近すると其の挙動は「ら線状形態」も出始める。また軌道線が連続な箇所と不連続な箇所とが混在している。
始点:Zo(黒い円))がZ^2マンデルブロ集合の境界線に一致してくると、点列の軌道はカオス状態になってくる。始点:Zo(黒い円))がZ^2マンデルブロ集合の境界線より大きくなると、点列の軌道は特異な不連続状の様態を
呈してくる。
また始点:Zo(黒い円))がZ^2マンデルブロ集合の『こぶ』の境界線に交わるところでは、点列の軌道は再び乱れ始める。
始点:Zo(黒い円))がZ^2マンデルブロ集合の境界線から外れていっても、極めて特異で不連続な形状の軌道が、Z^2マンデルブロ集合の「下腹部」に現れている。
いずれにしても、Z45~Z50の軌跡も極めて複雑な様態を呈していて、或る種の美しささえ感じさせる画像である。
----------------------------------------------







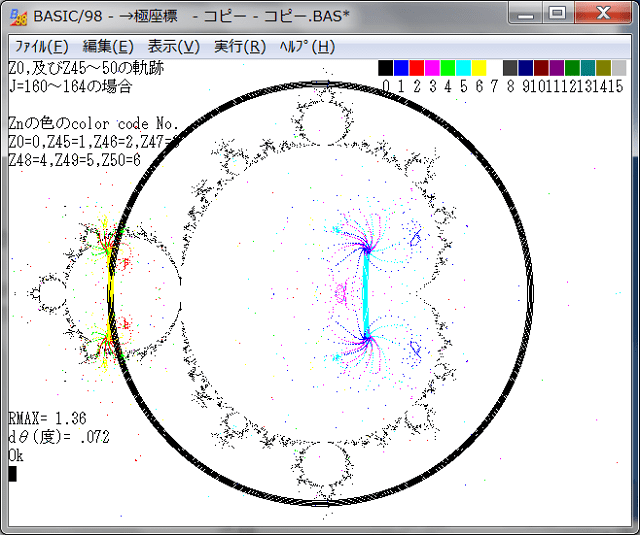


そこで色の区別がしやすい、0~6を使用して点列を表示する。即ち、
点列:Z0,Z1~Z45,Z46,Z47,Z48,Z49,Z50
にして、Z0→C=1(黒){注:Z0は点列の始点を表している}
Z45→C=1(青)、Z46→C=2(赤)、Z47→C=3(橙)、Z48→C=4(緑)、
Z49→C=5(青)、Z50→C=6(黄)として軌跡表示する。
極座標の距離パラメータJを固定して、角度θ=0→2π変化させて点列の各点の軌跡を調べる。その際、Jを5ずつ連続した画像を求めると、点列の挙動が分かり易くなると同時に画像としても面白いものが得られる。以下は、その画像である。
各画像に、Jの値を示してある。
***
下図から分かるように、Znのnが大きくなると前記事で予想したように、点列の挙動は更に複雑になる。特に始点:Z0(黒い円)が、Z^2マンデルブロ集合の境界線に接近すると其の挙動は「ら線状形態」も出始める。また軌道線が連続な箇所と不連続な箇所とが混在している。
始点:Zo(黒い円))がZ^2マンデルブロ集合の境界線に一致してくると、点列の軌道はカオス状態になってくる。始点:Zo(黒い円))がZ^2マンデルブロ集合の境界線より大きくなると、点列の軌道は特異な不連続状の様態を
呈してくる。
また始点:Zo(黒い円))がZ^2マンデルブロ集合の『こぶ』の境界線に交わるところでは、点列の軌道は再び乱れ始める。
始点:Zo(黒い円))がZ^2マンデルブロ集合の境界線から外れていっても、極めて特異で不連続な形状の軌道が、Z^2マンデルブロ集合の「下腹部」に現れている。
いずれにしても、Z45~Z50の軌跡も極めて複雑な様態を呈していて、或る種の美しささえ感じさせる画像である。
----------------------------------------------