画像作成条件は以下のとおり。
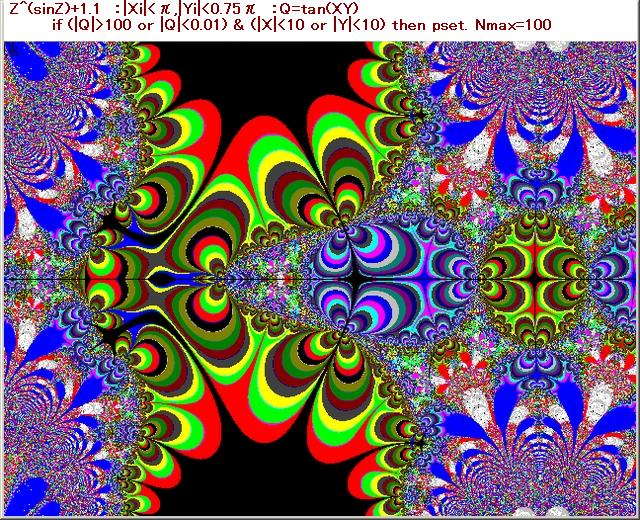
・複素関数:Z^(sinZ)+C で、C=0.1,0.3,0.7,0.9,1.1の6種類。
・N-loop脱出条件:Q=tan(XY),|Q|>100 or |Q|<0.01
・pset条件: |X|<10 or |Y|<1
--------------------------------------------





--------------------------------------------
注:下の4番目の画像(C=0.7)に顕著に分かるように、“噴火連山”が存在している(“噴火連山”については記事010を参照)
・複素関数:Z^(sinZ)+C で、C=0.1,0.3,0.7,0.9,1.1の6種類。
・N-loop脱出条件:Q=tan(XY),|Q|>100 or |Q|<0.01
・pset条件: |X|<10 or |Y|<1
--------------------------------------------






--------------------------------------------
注:下の4番目の画像(C=0.7)に顕著に分かるように、“噴火連山”が存在している(“噴火連山”については記事010を参照)




















































