今更ながら、微分積分。

最近、コンビニには、


「ちょっと、取っ付きにくいな・・・」と


思わせる題名の本がチラホラ見かける。


特に、「相対性理論」やら「量子論」とか・・・。

書店に行って、まず手には取らない本の『題名たち』だが、

さすがはコンビニ。

内容は至って「簡単」・「簡潔」に書いてある。

まぁ、？？？と思うところはあるが、面白く読みきった。


で、その？？？の中に微分積分的な表現がチラホラ。


正直、高校時代、聞いた事はあったが、その程度だ。

なにせ、自慢じゃないが、高校一年の１学期に、

何故か「分数」を復習しているクラスがあったくらい。

この時ばかりは、正直　『唖然』　としたが。


それは、さておき。

微分積分に何故か興味が出てきた。

通常、高校で教えるのは、公式の暗記と、その解き方くらい。

自分の性格上、ディープな所まで知りたくなってしまうので

詳しく考察する事にしてみた。

大体、学生の時は、

とりあえず、

グラフが書けて、式が暗記できてれば、

それで「ＯＫ」だからな。

そうゆう教育もどうか？と思うが。


とりあえず、簡単に考えると

微分→細かい変化

積分→大まかな変化

といった感じらしい。


・・・・・・・。


ふーぅ。


どうやら、１次関数グラフから思い出す必要があるな。


１次関数なんて、中学校以来思い出した事も無かったが。

えーと。

確か・・・縦軸が「Ｙ」で、横軸が「Ｘ」だったかな？

式で書けば、

「ｙ＝aｘ＋ｂ」

切片が通過点で、

『デカルト法線』　で表すと、

傾きが、（Ｘ，Ｙ）グラフの傾斜度って事だな。

「ｂ」　が切片で　「ax」　が傾きって事だよな。

と、ここまでは良いのだが。


ちょっとまて。


なんかおかしい・・・。
例えば、

　『ｙ＝２ｘ＋１』　は、

切片が　『１』　で、

傾きが　『２』　って事だよな・・・。



切片が　『１』　だから、ｙ軸の　『１』　を通るのは理解できる。

しかし、なんで、傾きが　『２ｘ』　なのに、

ｙが２増えるんだ？


なんか、


前にもつまづいたような・・・。


まぁ、いいや。この際だから、トコトンつまづこう。


えーっと、とりあえず、


「ｙ＝２ｘ＋１」


　を解いて


－ｙ／２ｘ＝１


で、


－２ｘ＝ｙ

ｘ＝－ｙ／２


って事か？


・・・・んーっ？？？


なんか変だ・・・。

多分こうじゃないな。


まず、「ｙ＝２ｘ」とは何かだ。


そうだ、

試しに『１』を、代入してみよう。


ｙ＝２×１　だと

ｙ＝２　になる。





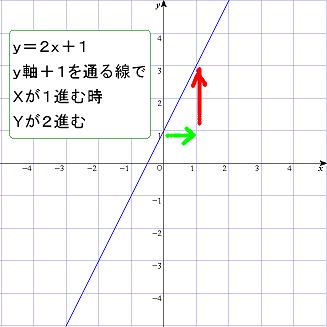
まてよ・・・。


「ｘが１」の時、「ｙが２」になってるって事か。


・・・・・・・。

あー・・・。なるほど。

『ｙ＝２ｘ』　ってのは

Ｘに対して、Ｙがどうなの？って式なのね。

それと、

ｙ＝２ｘ＋１の『＋１』は、

ｙの高さが変わるって事だ。


はぁ。


って、

微分積分までは、


まだまだ遠いな・・・・・。


時間はある。じっくりやろう。