「次は微分よ」
「微分ってなあに?」
「なめらかな曲線の接線を求めることよ」
「ぼくの体もマミの体もだいたいなめらかだから、だいたいどこでも接線が求められるのかな」
「そうね。…でも、こうやって下敷きを当ててもホントは1点でしか接しないと思わない?」
「そりゃそうだ。直線、水平な面なんてないから、なめらかってことはどこでもちょっとずつ変化してるってことだからね」
「うんうん、その点での変化率が微係数で、それを一般的に求めるのが微分なのよ」
「変化率と一緒ならぴったり接するわけか」
「微分の定義はこうよ」
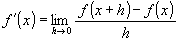
「ふうん。だんだん階段の刻みを小さくする感じだね」
「そうね。ちょっと練習にf(x)=x^3+2x^2+3x+4を微分しましょうか」
「え?ぼくがやるの?…しょうがないなぁ。
df(x)/dx=lim{(x+h)^3+2(x+h)^2+3(x+h)+4-(x^3+2x^2+3x+4)}/h
=lim(3x^2h+3xh^2+h^3+4xh+2h^2+3h)/h
=lim(3x^2+3xh+h^2+4x+2h+3)
h→0だから、
=3x^2+4x+3 だね」
「正解よ。こういうx^nの項からなる多項式の微分は計算すればいいから簡単なの。でも、そうじゃない三角関数や指数関数といった超越関数の微分をきちんと理解するのはけっこうむずかしいの」
「ふうん。で、どうやってするの?」
「三角関数は加法定理とh→0の時にsin(h)/hが1になることがわかっていればできるわ。くわしくはこのページを見て」
「手抜きだね。確かに面倒だけど。sin0=0、cos0=1だよね。はさみうちにするわけか。テクニカルだけど、イメージは湧いたよ」
「内接円・外接円で円周率πを詰めていくのと同じ感じ。微分と積分ってこういうことなんだけど。で、(sinθ)'=cosθ、(cosθ)'=-sinθになるの」
「ちょっと待って。…sin(θ+π/2)=cosθ、cos(θ+π/2)=-sinθじゃない?」
「そう、そこがポイントなの。サインとコサインの微分って直角に回転すること、π/2位相をずらすことなの」
「なるほど…わかってきたよ」
「次は指数関数の微分だけど、これもこのページを見ればいいかな」
「微分のh→0をeの式のn→∞に当てはめるために逆数を取ったわけか。スカスカの整数を実数に簡単に拡張できる理由があまり納得できないけどね」
「まあ、そこはわかったことにしておいて。…で、こうなるわけ」

「あれ?微分しても変わらない」
「そう、何度微分しても同じ。だから、積分しても原始関数としては同じ。だから、すごく便利。これがeが自然対数の底って呼ばれる所以よ」

「底が2と3のグラフと並べておくわ。(0,1)での微係数が1になってるでしょ。もちろん他の点でもyの値と全部同じ」
「不思議だな。こんな数があるなんて。…しかも、3よりちょっと小さい数だなんて」
「あなたが不思議って言うのもめずらしいわね」
「だって、πは3よりちょっと大きい数だよ」
「そうね。代数的に書けない無理数を超越数っていうけど、その代表のπとeがこんなに近いところにあるのは不思議ね。しかも指数関数と三角関数で密接に結びついてる…」
「微分ってなあに?」
「なめらかな曲線の接線を求めることよ」
「ぼくの体もマミの体もだいたいなめらかだから、だいたいどこでも接線が求められるのかな」
「そうね。…でも、こうやって下敷きを当ててもホントは1点でしか接しないと思わない?」
「そりゃそうだ。直線、水平な面なんてないから、なめらかってことはどこでもちょっとずつ変化してるってことだからね」
「うんうん、その点での変化率が微係数で、それを一般的に求めるのが微分なのよ」
「変化率と一緒ならぴったり接するわけか」
「微分の定義はこうよ」
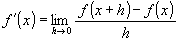
「ふうん。だんだん階段の刻みを小さくする感じだね」
「そうね。ちょっと練習にf(x)=x^3+2x^2+3x+4を微分しましょうか」
「え?ぼくがやるの?…しょうがないなぁ。
df(x)/dx=lim{(x+h)^3+2(x+h)^2+3(x+h)+4-(x^3+2x^2+3x+4)}/h
=lim(3x^2h+3xh^2+h^3+4xh+2h^2+3h)/h
=lim(3x^2+3xh+h^2+4x+2h+3)
h→0だから、
=3x^2+4x+3 だね」
「正解よ。こういうx^nの項からなる多項式の微分は計算すればいいから簡単なの。でも、そうじゃない三角関数や指数関数といった超越関数の微分をきちんと理解するのはけっこうむずかしいの」
「ふうん。で、どうやってするの?」
「三角関数は加法定理とh→0の時にsin(h)/hが1になることがわかっていればできるわ。くわしくはこのページを見て」
「手抜きだね。確かに面倒だけど。sin0=0、cos0=1だよね。はさみうちにするわけか。テクニカルだけど、イメージは湧いたよ」
「内接円・外接円で円周率πを詰めていくのと同じ感じ。微分と積分ってこういうことなんだけど。で、(sinθ)'=cosθ、(cosθ)'=-sinθになるの」
「ちょっと待って。…sin(θ+π/2)=cosθ、cos(θ+π/2)=-sinθじゃない?」
「そう、そこがポイントなの。サインとコサインの微分って直角に回転すること、π/2位相をずらすことなの」
「なるほど…わかってきたよ」
「次は指数関数の微分だけど、これもこのページを見ればいいかな」
「微分のh→0をeの式のn→∞に当てはめるために逆数を取ったわけか。スカスカの整数を実数に簡単に拡張できる理由があまり納得できないけどね」
「まあ、そこはわかったことにしておいて。…で、こうなるわけ」

「あれ?微分しても変わらない」
「そう、何度微分しても同じ。だから、積分しても原始関数としては同じ。だから、すごく便利。これがeが自然対数の底って呼ばれる所以よ」

「底が2と3のグラフと並べておくわ。(0,1)での微係数が1になってるでしょ。もちろん他の点でもyの値と全部同じ」
「不思議だな。こんな数があるなんて。…しかも、3よりちょっと小さい数だなんて」
「あなたが不思議って言うのもめずらしいわね」
「だって、πは3よりちょっと大きい数だよ」
「そうね。代数的に書けない無理数を超越数っていうけど、その代表のπとeがこんなに近いところにあるのは不思議ね。しかも指数関数と三角関数で密接に結びついてる…」