葉っぱのつき方から黄金比へ

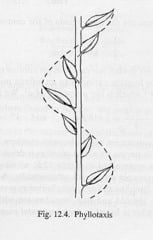
　これまで２回にわたって黄金比とフィボナッチ数列のごく簡単な性質を見てきたので、あと何回かで自然と芸術においてこれらがどのように現われているか（あるいは現われていないか）を見たいと思います。
　まず上の図のような葉っぱがらせん状についていく場合を見てみます。もちろん植物によっていろんなタイプがあるんですが、上から見ると例えばウラジロチチコグサでは、このようになっています。



　２番目の葉っぱは７番目の葉っぱに重なって見えなくなっていますから、この場合は５枚の葉っぱが出る間に２回りしたことがわかるでしょう（もちろん１番目のが６番目ので隠れていないとかズレはありますし、その方が後での説明としてはいいんですが）。つまり2/5回転（＝144度）ずつずれて葉っぱが出て行くわけです。こうした規則性を葉序と言って、２枚で１回転（180度、この場合は上から見ると十字に見えますね）、３枚で１回転（120度）とか、いろいろありますが、主なものを上げると1/2、1/3、2/5、3/8、5/13などだそうです。これだけじゃなんのことかわからないので、フィボナッチ数列の最初の方を書いてみましょう。最初に１を２つ書いて、その２つを足して次の項を作っていけばいいんで簡単です。
　1,1,2,3,5,8,13……

　そうなんです。分母も分子もフィボナッチ数列に出てくる数（フィボナッチ数と言います）で、しかも分母と分子の関係は数列の一つおき（例えば3/8は５をはさんだ両側が分母、分子になっているということ）なんです。偶然でしょうか？

　いいえ。じゃあ、ふつうの人があまり知らないのに植物がフィボナッチ数列を知ってるんですか？　ある意味そうでしょうねｗ。まさか。……

　まあ、その説明は追々するとして、ちょっとわかりやすくしましょう。まず葉っぱは逆回りで考えているとしてみます。つまり2/5回転（144度）じゃなくて、3/5回転（216度）だと。こうすると、さっきの分数はこうなります。1/2、2/3、3/5、5/8、8/13。どうです？　隣り合う項が分母、分子になったでしょう？　なぜそうなるのかは簡単です。

　最初の関係は、a_n/a_n+2　ってことですが、これを1から引いて、
１－a_n/a_n+2　として、a_n+2＝a_n+1＋a_nの関係を使うと、
(a_n+2－a_n)/a_n+2＝a_n+1／a_n+2 となりますね。
　
　で、この分母、分子をひっくり返すと（逆数は）黄金比φ＝(1+√5)/2≒1.6180339887に収束する（だんだん近づいていく）んでしたね。これで植物は本音ではｗ、360度をφで割った角度約222.5度で葉っぱを出したいんじゃないかという予測ができます。ついでに言うと、φの逆数は前に述べたように0.6180339887…すなわちφから１を引いたもの（小数部分）になっています。
　
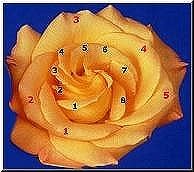
　たださっきのように数が少ないんじゃあ心もとないんで、もっといろんな例を挙げましょう。バラの花びらにも次のようにフィボナッチ数５と８が現われています。


　
　それ以上に注目されるのがらせん状になっていることで、次のcone flowerという花を見ると一目瞭然でしょう。





　このらせんの数は21、34となっていて、13の次とその次のフィボナッチ数です。有名なのはパイナップルやひまわりの例で、ぐぐれば簡単に出て来ますが、こうしたことをまとめて言うと植物はなぜだか222.5度が、つまりは黄金比がとても好きだということになるでしょう。

　その理由は例えば45度について見るとわかってきます。下の図は45度ずつ回りながら外に向かって点を100個置いていったものです。



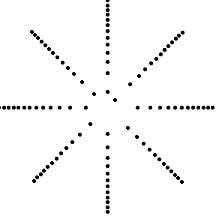
　当然、固まってしまいますね。これが葉っぱなら重なってしまって十分な日光が受けられませんし、種ならひしめき合って大きくなれません。じゃあ、222.5度ずつ同じ100個なら？　こうなります。



　ね？　見事にバラけるでしょう？ 植物の戦略が見えてきますね。……なんでこんなにうまくバラけるのかって？　正確に私も説明できるわけじゃないんですが、前回の最後に挙げた連分数を思い出してください。あれは黄金比の本質を表していて、全部が１だけでできている連分数だということは最も分数で表すことがむずかしい、つまり何回回っても同じところに来にくい数っていうことなんです。じゃあ、無理数の代表の円周率ならどうかって？　いい質問です。360度に円周率の小数部分0.14159を掛けた50.97度で回したものが次の図です。



　500個と2,000個のですが、やっぱり222.5度ほどは散らからずに明瞭ならせんパターンを描いたりして固まっていますね。ちなみに円周率の連分数の表現は古来からたくさんあるんですが、どれもφほどは単純じゃない、つまり分数で近寄ることが比較的容易なんです。