微分は積分よりも簡単である。
それは、微分の定義が明解であるからである。 定義と若干の公式さえ覚えておけば、微分は理解し易い。
よって、先ずは定義のみ記述しておく。
ちなみに、数学には定義と定理がある。 この二つを混同している人はいないであろうか?
国語辞書の問題であるが、
定義=ある概念の内容や言葉の意味を他の概念や言葉と区別できるように明確に限定すること(iPhone版大辞林より)
定理=公理に基づき、論証によって証明された命題(同上)
つまり、定義は決め事であり、定理は証明されたことである。 英語ならば、
定義=Definition
定理=Theorem
である。
定義は決め事なので、証明は要らない。 よって、定義さえ知っていれば、公式(定理の結果)は導出できるから、全部覚えなくて良いのである。
さて、微分の定義は変数xの関数がf(x)のとき、下のようなものである。フォントが違うことは容赦願いたい。 ちなみにf'(x)は関数f(x)の一階微分であることを表している。
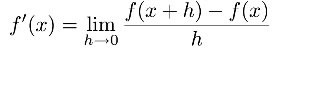
limはLimitの略で、極限を表す。 つまり、右辺の分母と分子にあるhができるだけ0(ゼロ)に近づいたときと言う意味で、h=0ではない。 微分の理解はこの極限がイメージできるかどうかが最も重要である。
極限がイメージ出来るようにならないと、微分はいつまでたっても理解できない。
次回は、この極限について、述べるつもりである。
それは、微分の定義が明解であるからである。 定義と若干の公式さえ覚えておけば、微分は理解し易い。
よって、先ずは定義のみ記述しておく。
ちなみに、数学には定義と定理がある。 この二つを混同している人はいないであろうか?
国語辞書の問題であるが、
定義=ある概念の内容や言葉の意味を他の概念や言葉と区別できるように明確に限定すること(iPhone版大辞林より)
定理=公理に基づき、論証によって証明された命題(同上)
つまり、定義は決め事であり、定理は証明されたことである。 英語ならば、
定義=Definition
定理=Theorem
である。
定義は決め事なので、証明は要らない。 よって、定義さえ知っていれば、公式(定理の結果)は導出できるから、全部覚えなくて良いのである。
さて、微分の定義は変数xの関数がf(x)のとき、下のようなものである。フォントが違うことは容赦願いたい。 ちなみにf'(x)は関数f(x)の一階微分であることを表している。
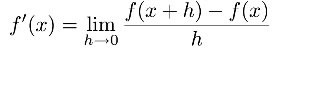
limはLimitの略で、極限を表す。 つまり、右辺の分母と分子にあるhができるだけ0(ゼロ)に近づいたときと言う意味で、h=0ではない。 微分の理解はこの極限がイメージできるかどうかが最も重要である。
極限がイメージ出来るようにならないと、微分はいつまでたっても理解できない。
次回は、この極限について、述べるつもりである。
















※コメント投稿者のブログIDはブログ作成者のみに通知されます