内角 ＋ 外角 ＝１８０° どうして？

北海道の小中学校は、夏休みが短く あと１週間も残っていないようです。

本州が 地獄的な猛暑の時に、北海道は比較的涼しい夜がやってきますので

勉強もはかどるのではないか？・・・と思いますが。

さて、前回の問題。

その前に、内角と外角の関係について

前回ヒントに出しました 内角と外角の図を見て、

正多角形の外角は、簡単な計算でわかるんだ～と、気がつきましたか？

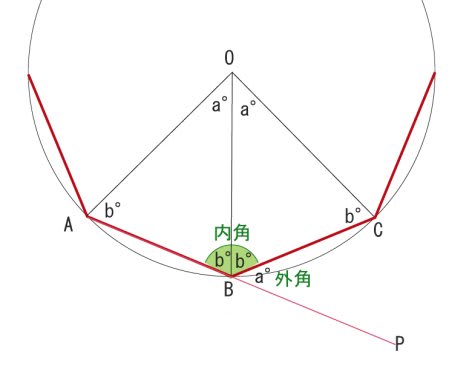
△ＯＡＢも △ＯＢＣも ２等辺三角形で、合同です。

その底角を ｂ°とすると、内角は ２ｂ° で、

２ｂ°は△ＯＡＢの内角の和１８０°から a°を引いた角度です。

２ｂ＝１８０－a

そうしますと内角∠ＡＢＣは２ｂ°ですから 外角∠ＣＢＰは、

１８０－２ｂ で、外角∠ＣＢＰ＝∠ＡＯＢとなります。

ここまで、分かるかな？

これはもう大発見なわけで、正多角形の外角は

辺の数をｎとしたとき、３６０÷ｎ で分かってしまうわけです。

 

正六角形の外角は、 ３６０÷６＝６０  で、６０°

正八角形の外角は、３６０÷８＝４５   で、４５°

正十角形の外角は、３６０÷１０＝36  で、３６°

もういいか・・・・

そして前回の問題

正多角形で、その内角が 外角の７倍であった。

この正多角形の辺の数は、いくらか？

これを式にしますと。

２ｂ＝a×７、  ２ｂ＝１８０－a より

１８０－a ＝7a

これを解いて、a＝４５/2=２２．５

正多角形の辺の数は、３６０÷２２．５＝１６  より   答え  １６

＊360÷45/2＝３６０×２/４５＝（３６０/４５）×２ として 約分すれば計算は楽ですね

 

 

もうこれで、正多角形の外角は、暗算でも分かるようになってきました！

正多角形の内角は、先に外角を暗算してから、１８０－外角で計算した方が

早いかも～

 

内角 と 外角 って 何だっけ？

内角 と 外角  って、言葉は聞いたことがあるけど

何だかよく分からない～  と言う人！

辞書などには、このように書いてあります。

多角形の各頂点において，それを端点とする二つの辺が多角形の内部のほうで作る角をその頂点における多角形の内角という。

内角が2直角以下のとき，その補角のことを外角という

 

これで、すぐに分かった人は問題はありませんが、こんなこむつかしい表現はジンマシンが出ちゃう～

という人のために もう少し噛み砕いて言いますと

 

三角形とか、四角形とか 多角形と言われる図形で

そのうちの１つの頂点から見て、内側にできる角を 内角

内角とは反対側にあって外側にできる角から１８０°引いた角を 外角 と言います。

但し、内角が１８０°以内のときだけ外角があります。

 

と、これならちょっとは分かりやすくなったでしょうか？

 

多角形で、内角の大きさが全部等しい 正多角形のときには

内角と 外角の 大きさが、辺の数で決まります。

今回は、そのことを使った問題

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

正多角形で、その内角が 外角の７倍であった。

この正多角形の辺の数は、いくらか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ひゃ～たった２行の 問題ですが、

わかりますか？

 

ヒントに  図を ひとつ

これ、ほとんど答えですが・・・・・

 

 

２５％増し って どういうこと？

前回の問題。

Ａさんは、ある本を読むのに 毎日同じページづつ読むことひしていたのですが、

３日目から、２５％増しで読んだので 予定よりも３日早くその本を読み終えました。

はじめは何日で読み終える予定でしたか。

ヒントに少し 図を描きましたが、

これを もう少し くわしく描きますと

このような図が 描ければ  式を考えるのは 分かりやすくなります。

自分で分かったら、次は誰かに説明することを考えてください。

 

よく出る！ ２５ の 問題 ～ 中学入試問題より

算数でも、数学でも ２５  という数字は よく使われます。

２５ を基本に考えると、恐ろしく計算が速くなります～という記事は

以前にも書きました。（５月１８日の記事参照）

 

その２５を使った問題。

中学 入試問題より

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

Ａさんは、ある本を読むのに 毎日同じページづつ読むことひしていたのですが、

３日目から、２５％増しで読んだので 予定よりも３日早くその本を読み終えました。

はじめは何日で読み終える予定でしたか。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

さて、式はどうする？ という前に

これを図に描くとどうなるのか？

これから考えてみましょう～

 

ここで重要な数字は ２５％ と 早く読み終えた分の３日。

ここをどう考えるか？で、２５％増しで読んだ日の日数が分かるのですが・・・・・

 

流れる川 と 船 の 速度の問題 解説～

前回の問題、

川に沿って８ｋｍはなれた２つの町を往復する船があります。

通常、この川を上るのに２時間、下るのに４０分かかります。

増水で川の流れの速さが１．５倍になったため、通常の２倍の速さで川を上りました。

このときかかる時間は何分ですか。

次のように考えます。

 

 

ここ数ヶ月  日本各地で 大雨による被害が出ています。

本日も 「かって経験したことがないような大雨」という言葉を使って

気象庁から警報が出ておりました。

皆さま、充分お気を付けください。