図形を見て、規則性を考えて式を作り
計算して答えを見つける。
文章で書きますと、いかにもカンタンな作業に思えますが
どうして どうして 一筋縄ではいかないものです。
=================================
1つの円周上に、等間隔に並んだ点が
N個あります。
このN個の点を結ぶ線を書いたとき、その線の数は276本になりました。
点の数は いくらだったのでしょうか?
=================================
文章だけで、図が描かれていません。
円周上に等間隔に並んだ点で作られる図形は 正多角形です。
たとえば、点の数が6の 正6角形の場合は、
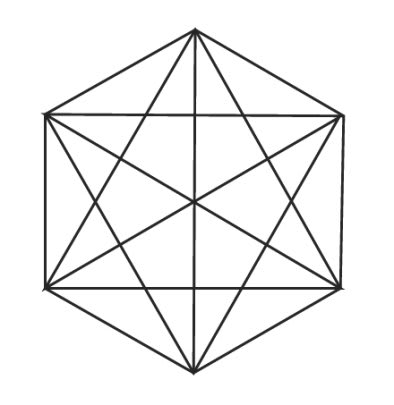
このようになりますね。
さて、これは円周上の点と点を結ぶ線の数が15本あります。
276本だと、とりあえずいろんな多角形を描いて線を引いてみて・・・
という作業では、日が暮れてしまいそうです。
線の数と、点の数の関係を式にすることが早道のようです。









