内角 と 外角 って、言葉は聞いたことがあるけど
何だかよく分からない~ と言う人!
辞書などには、このように書いてあります。
多角形の各頂点において,それを端点とする二つの辺が多角形の内部のほうで作る角をその頂点における多角形の内角という。
内角が2直角以下のとき,その補角のことを外角という
これで、すぐに分かった人は問題はありませんが、こんなこむつかしい表現はジンマシンが出ちゃう~
という人のために もう少し噛み砕いて言いますと
三角形とか、四角形とか 多角形と言われる図形で
そのうちの1つの頂点から見て、内側にできる角を 内角
内角とは反対側にあって外側にできる角から180°引いた角を 外角 と言います。
但し、内角が180°以内のときだけ外角があります。
と、これならちょっとは分かりやすくなったでしょうか?
多角形で、内角の大きさが全部等しい 正多角形のときには
内角と 外角の 大きさが、辺の数で決まります。
今回は、そのことを使った問題
====================================
正多角形で、その内角が 外角の7倍であった。
この正多角形の辺の数は、いくらか?
====================================
ひゃ~たった2行の 問題ですが、
わかりますか?
ヒントに 図を ひとつ
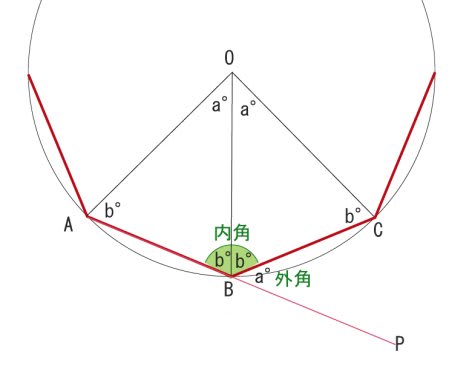
これ、ほとんど答えですが・・・・・









