宇宙と宇宙をつなぐ数学 加藤文元 ABC予想を解き明かすIUT理論をめぐる決定版解説

これを書いている2020年4月、「数学の超難問ABC予想が証明された」というニュースがかけめぐった。京大数理解析研究所の望月新一教授の論文が発表から8年近くを経て専門誌に掲載されることが決まった。評者はワシントンにいた1990年代半ば、数学の超難問「フェルマー予想」を解決したプリンストン大のアンドリュー・ワイルズ教授にインタビューしたことがある。そのことをあらためて思い出した。望月教授に関しては、東工大の加藤文元教授の解説書があったことを思い出し、すぐにアマゾンで手配したが品切れ。数学書でそんなことがあるのかと驚いたが、幸い1週間ほどで入手できた。2019年4月発行ながら、今年4月で9刷と版を重ね、読者の関心の高さを物語っている。
加藤教授は啓蒙書を多く手がけ、望月教授の難解きわまるIUT(宇宙際タイヒミュラー)理論のよき理解者だ。しかも京大時代には望月教授と親交があったそうで、最良の解説者だろう。300頁ほどの入門書ながら、極力数式を排し、イラストも多用して数学の知識が乏しい読者に理解してほしいという熱意がわかる。もちろん、IUT理論はすこぶる難解で、読了しても理解できたとは到底、言えないが。
望月教授は飛び抜けた数学者によくある早熟の天才タイプだ。父親に連れられて5歳で渡米し、東海岸にある英才高校を出たあと、16歳の若さで数学では全米トップといわれるプリンストン大に飛び級入学した。19歳で大学を卒業し、大学院に進学して23歳で学位を取った。大学での指導教授は数学界のノーベル賞といわれるフィールズ賞受賞者のゲルト・ファルティングス教授。帰国してすぐに京大数理解析研の助手に採用され、32歳の若さで教授に就任した。国内ばかりか海外の学会にもほとんど顔を見せず、マスコミ取材も拒否しているとあって、さまざまな伝説が生まれるのも当然のことだろう。だが、加藤教授によると、焼肉が大好物でテレビドラマにも詳しく、気さくな性格という。加藤さんはわざわざ望月教授のそういった側面を明かす。噂が一人歩きして、人柄が誤解されかねないことへの配慮だろう。
本書には望月教授の「刊行によせて」という巻頭言も掲載されている。「宇宙際タイヒミュラー理論」に関するセミナーを加藤氏と始めたとき、「まさか十数年後に、加藤氏が一般社会向けに理論を解説するという形の書籍を書き、その巻頭言を依頼される日が来るとは夢にも思っていなかった」。望月教授はこの理論による発想の転換が数学界に与えるインパクトについて、大航海時代のヨーロッパでガリレオが地動説を唱えたことや20世紀前半のドイツ語圏で、アインシュタインの相対性理論や量子力学の誕生など、パラダイムシフトと呼ばれる科学史上の大発見や大変革になぞらえている。そのうえで、「本書が数学的な理論と社会を繋ぐ、有意義な『緩衝材』・橋渡し役としての機能を果たす可能性に、大変期待を寄せている次第です」と書いている。本書は、望月教授の唯一の「公認本」といえるのだろう。
望月教授の論文が最初に発表されたのは8年前の2012年8月30日、自分自身のホームページ上でだった。論文は全部で4編で分量は500頁を超える。そこには、「『ABC予想』という非常に有名で、数学にとって極めて重要な予想を解決した」と主張されていた。最初は世界で数十人という狭い数学コミュニティで共有されただけだったが、9月に入るとNYタイムズなど海外の有力メディアが取り上げ、国内でも共同通信が配信して広がり始めた。ただこの段階では正式に数学の論文誌に掲載されたわけではない。今回、ニュースが広がったのはこの論文が専門誌に受理され、公式に論文として認められたからだ。だが、この段階でも世界の数学界が「ABC予想は解決された」と認めたわけではない。今後数年かそれ以上かけて、世界中の専門家が論文を精査し、間違いがないかどうかを検証する。しかし、先行論文を参照する必要もあり、合計した論文の分量は1000頁以上になる。しかも、論文はきわめて斬新な数学の枠組みに基づいて書かれていて、専門家でも理解が容易ではないという。
加藤教授は、革命的な新理論についてその特徴を一般にもわかりやすい言葉で解説しようと努める。「IUT理論は、一般的な数学のパラダイムの枠内では語れない、まったく新しいフレームワークと言語・概念体系を基盤にして構築されている」「通常のコミュニケーションの手段である講演やセミナートークといった方法では、そもそも言語体系が異なるので、通常のように議論を始めることができない」「むしろ個人的、あるいは少人数による双方向的な会話体のコミュニケーションを積極的に積み重ねることで、少しずつ、理解者の数と層を厚くしていくというのが最良の方法と考えられる」。これだけ読むとIUT理論を理解するのは常人はむろんのこと、専門の数学者でさえ、至難の技としか思えなくなってくる。
だが、理論の伝道師という難役を引き受けた加藤教授は、数学の成り立ちを起点にして、この理論をできる限り平易に解説しようと試みる。何十年も前の評者の学生時代は数学を純粋数学と応用数学に分ける考え方があった。理学部数学科は純粋数学で、工学部の数理系学科は応用数学といった具合。だが、純粋数学でも応用価値の高いものは多いし、逆もまた真なり。評者は工学部出身だが、当時は多くの工学部生が数学のレベルでは理学部にかなわないと感じていた。だが、コンピューターや関連理論の発達で、そうした区別も意味をもたないことがはっきりしてきた。最近では最先端の数学や数学モデルを経済学や金融工学などさまざまな他分野に応用する動きが盛んだ。
加藤教授は数学者の仕事について、わかりやすい説明をしている。興味のある方は本書を読んでいただくとして、そろそろ宇宙際タイヒミュラー理論に移ろう。タイヒミュラーというのは20世紀前半に活躍したドイツの数学者だ。「タイヒミュラー理論は、『タテとヨコ』とか『長さと角度』とか、とにかく2つの次元をもつ図形を相手にします」「とりあえずは例として、ただの平面を考えてもらって結構です。ただし、そこには『複素構造』というものが入っていなければなりません」「複素数を知らない人は、ちょっと難しいことかもしれませんが、こういう風に考えましょう。つまり、この平面にはタテとヨコを独立に扱うことのできない、総合的な構造が入っているということです」「例えば、複素平面では横軸は実軸で、縦軸は虚軸と呼ばれるもので、複素数という一つの全体の中での役割が決まっています。ですから、ただの平面のように、タテとヨコを独立な次元として扱うことはできません」「この『2つの次元が一蓮托生に結びついている状態』を、望月教授の用語に倣って、これからは『正則構造』と呼ぶことにします。正則構造が入っている図形においては、一方の次元を固定したまま、他方の次元を変化させるというようなことは許されません。それは正則構造を破壊するからです」「タイヒミュラー理論は、この正則構造を敢えて(上手に)破壊することで、図形を変形させることを積極的に行う理論です。これによって、考えている図形の変形をすべて書き出すことができますし、その変形全体がなす空間を考えることができます」。その骨子は「『2つの次元が一蓮托生であるさま(正則構造)を破壊し、一方の次元を固定して、他方の次元を伸び縮みさせる変形をすることで、さまざまな図形を作り出し、それらの相違を定量化する』というものです」。言葉だけではちょっとイメージがつかみにくいが、一蓮托生は望月教授がよく使う言葉だという。
「IUT理論を構築する途上の望月教授は、だれもまだ通ったことのない山道を、一人で一歩一歩登っていく冒険家にも喩えられるかもしれません。それはだれも通ったことがないのですからだれも道案内することはできません。各所で見渡せる景色や、自然のちょっとした変化も見落とさず、少ない情報を大切に利用して進まなければならないのです。その一歩一歩が、果たして正しい方向を向いているのかは、だれにもわかりませんし、望月教授本人にもわからなかったことは、さぞかし多かったことでしょう」。では望月教授は何をもとに歩みを進めたのだろうか? 加藤さんは「それは『自然であること』とでも言えるものではないかと思うのです」と書いている。「多くの場合、数学の理論を構築する上でGPSの役割(注:道案内)を果たすのが、『自然であること』についての鋭敏な直感なのだ、というわけです」。明確な説明とはいえないだろうが、何となくわかるような気もしてくる。
それでは理論の名前についている「宇宙際」とはどういう意味なのだろう。国際が国と国とをつなぐという意味なら、「宇宙際」は異なる宇宙をつなぐという意味のはずだ。この場合の宇宙は数学的宇宙だから数学的約束事が異なる空間をつなぐということだろう。
そもそもABC予想とは、どんな予想なのだろう。1995年に解決されたフエルマー予想は、Xのn乗+Ýのn乗=Zのn乗という方程式の場合、nが3以上であればX、Y、Zが自然数(正の整数)の組としては存在しないという予想だった。一見、簡単そうに見えるが17世紀の大数学者フェルマーが問題として提出して以来、300年以上も解決されなかった。多くの数学者が頭を悩ませるなかで、数学が大きな進歩を遂げていった点でも特筆される。
一方、ABC予想は非常に新しい。問題が提出されたのは1985年。ヨーロッパの2人の数学者によってだ。ABC予想にも「ABCトリプル」と言われる3つの自然数が登場する。まず互いに素である2つの自然数aとbを考える。a+b=cとする。さらにabcを構成しているすべての素数の積を考えてみる。たとえばaを5、bを7とするとa+b=12で、cは12となる。12は2の2乗X3だから、ここで現れるすべての素数は2、3、5、7で、それらを掛け合わせた積dは210。この場合、dはcより大きいが、多くの場合、dはcより小さい。例えば、aを1、bを8とするとcは9、abcを構成するすべての素数の積dは2X3=6で、cよりも小さい。「実際にいろいろと計算してみると、ほとんどの場合ではdの方がcより大きく、cの方がdより大きくなるケースは非常にまれであることがわかります」。実際、コンピューターによる計算で、cが4桁の場合、可能なABCトリプルの個数は約1500万通りあるが、dがcより小になる例外的トリプルは120個しかない。cが5万未満の範囲だと、可能なABCトリプルは約3億8000万個もあるのに、例外的トリプルは276個しかないという。「ABC予想とは、この例外的トリプルが『とても少ない』という状況を数学的に定式化することによって立てられた予想です」。
加藤教授はIUT理論の革新性について、言葉やイラストでやさしく説明してくれる。宇宙際という考え方は数学的約束ごとのまったく異なる世界をつなぐという意味だが、それを言葉で説明するのはなかなか難しい。加藤さんは世界が異なることをジグソーパズルで説明する。ジグソーパズルは一枚の絵を細かなピースに分け、元の絵を復元していくが、元の絵が異なる大きさだった場合、ピースはうまくくっつかない。下のイラストはそれを説明している。形は同じでも、元の絵の大きさが異なるので、そのままでははまらない。195頁(上)と273頁(下)にあるイラストだ。
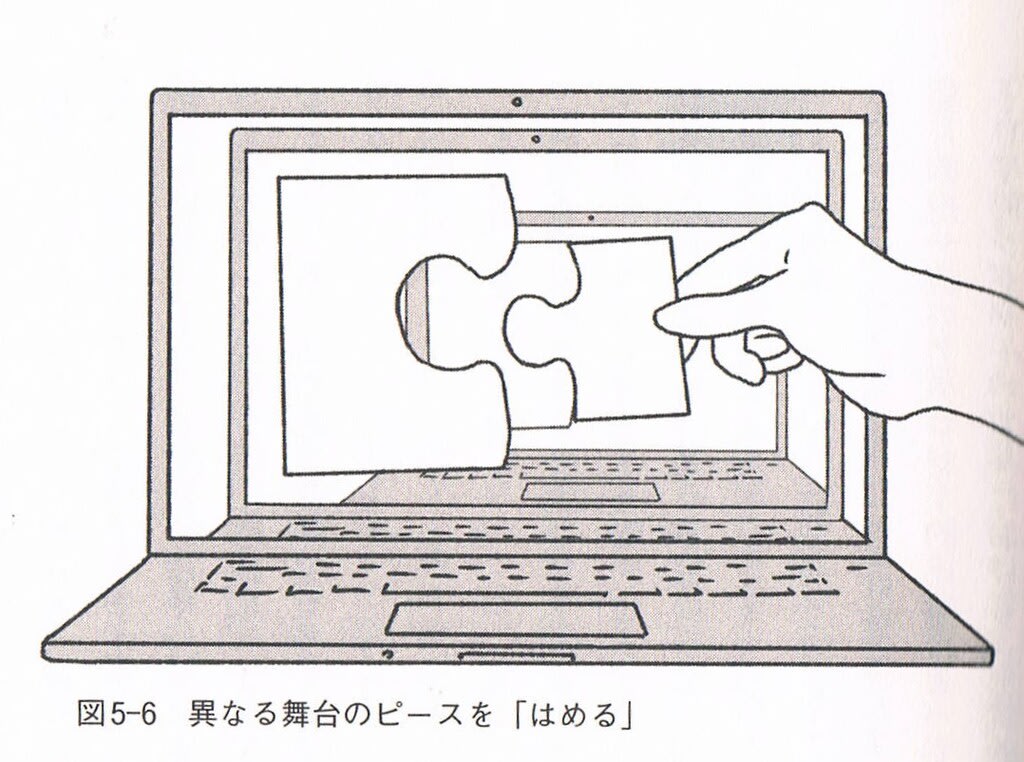
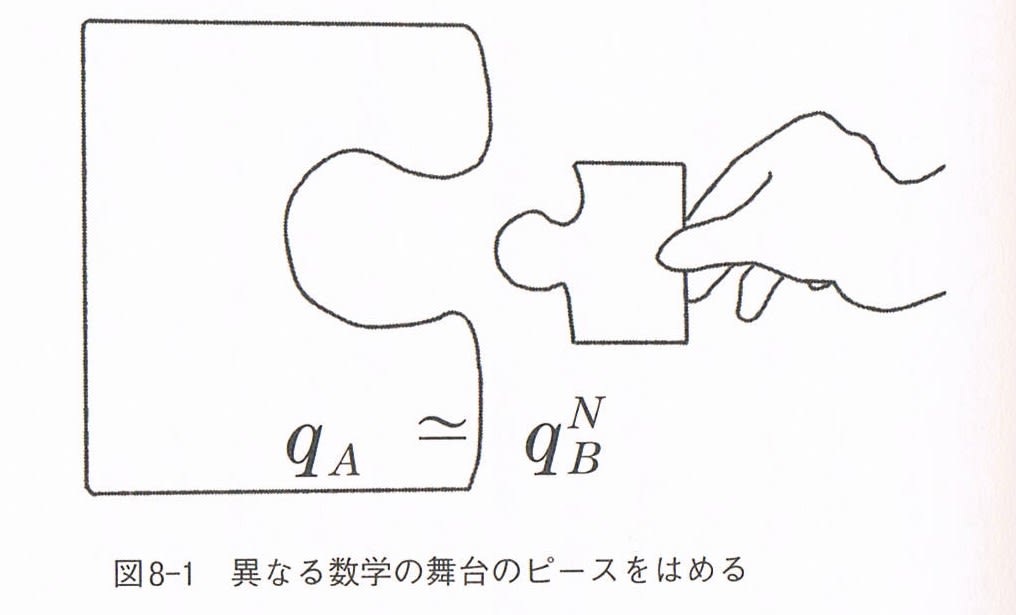
ジグソーパズルの世界が異なるなかで、パズルを完成させようと試みているイメージが伝わるだろうか。上のイラストではディスプレイが同じ形の図形を映し出しているが、それぞれのディスプレイは異なる世界をイメージしている。
加藤さんは、「IUT理論が、その基礎に持っているキーワードは「伝達・復元・ひずみ」の3つだとし、「これらのキーワードは、『IUT的な数学』が『従来の数学』と抜本的に異なっていることから生じるものです」と説明する。また、「これらの言葉は複数の数学の舞台、つまり数学をするための一式の世界を複数用意するという、IUT理論による史上初めての試みがあってこそ、重要なのでした。つまり、これらのキーワードは『IUT的な数学』が『従来の数学』と抜本的に異なっていることから生じるものです」。「ABC予想が解決されたとなると、この関連の整数論や数論幾何学の諸分野へのインパクトは甚大です。ABC予想が証明されてしまうと、現代数学の景色が一変してしまう、と言うことだってできるでしょう」とその意義を強調する。
そうした説明のなかで、加藤教授は数学における「予想」の重要性についても丁寧に説明してくれる。フェルマー予想は「それそのものが数学的に深く、あるいは美しかったということよりも、それが歴史上の数学者を駆り立てて、多くの数学の深い理論をつくらせたという意味では、とても重要な予想でした。なにしろ、シンプルで難しい予想でしたから、多くの数学者により注目されてきました。そして、それを解こうと試みる中で、彼らがいろいろな数学上のアイデアを出し、それが一つの大きな理論となって結実する、ということも多々ありました」「その意味で、『予想』はただ単に『正しさが保留されている命題』という意味合い以上の、重要な役割を担っています。それは数学者に深い洞察への誘いとモティベーションを与えるのです。(中略)それは数学を進歩させ推進させるための原動力にもなっています」。
ここまで読んで、評者には腑に落ちる経験があった。それは今から25年前、フェルマー予想を解決したワイルズ教授をプリンストン大に訪ねた時だった。大学の広報に顔を出すと、「カメラを持っていますか?」と聞かれた。「もちろん」と答えると、「教授は非常にシャイな方なので、カメラを持っていてはインタビューできません」と取り上げられてしまった。アメリカでも初めての経験で本当に驚いた。実際のワイルズ教授はセーター姿の穏やかなイギリス紳士で、世紀の難問を解いた人とは思えなかった。最近、うれしかったことはと聞くと、「風邪を引いて少し自宅にいたので、家族と過ごせてよかった」と答えるなど家庭的で好感の持てる人だった。驚いたのは幅2㍍以上ありそうな大きな机の全面に20㌢ほどの高さで、論文の別刷りなど資料が山積みになっていたことだ。「資料探しに困りませんか?」と聞くと、「まったく問題ない」との返事。「今回の業績を理解できる数学者は世界にどれくらいいるのでしょうか?」と聞くと「十数人くらいかな?」。心地よい興奮を感じながら、インタビューを終えた。
次に数学科の同僚である志村五郎教授の部屋を訪ねた。志村教授も世界的に著名な数学者。だが、こちらは机の上にまったく物がない。あまりの落差に当惑していると、いきなり、「これを読んでおいて」と英文の手紙を差し出された。あわてて読むと、NYタイムズ科学部長宛ての激烈な抗議文だった。その数週間前、NYタイムズは一面でフェルマー予想を解決したワイルズ教授の業績を大きく取り上げ、科学面でその内容を詳述していた。フェルマー予想は、志村教授とやはり日本の谷山豊博士による「志村・谷山予想」を利用して解決に導いたが、タイムズはこれを「谷山・志村予想」と書き、志村教授の怒りをかった。「あの仕事は私の名前が先に来るべきで、これは大きな間違いだ」。そのとき、印象的だったのは、「数学者は問題をつくる人とそれを解く人がいる。あなたはどちらの方が重要だと思うか?」と聞かれたことだ。もちろん、ワイルズ氏は問題を解く人、志村氏はつくる人だ。言外にワイルズ氏より自分の方が数学者としては圧倒的に優位だという自負があるのは明白だった。本書を読んでみて、問題をつくる(数学的予想を出す)ことの重要性がほんの少しわかったような気がする。志村教授は2019年5月、89歳で他界された。谷山氏は将来を嘱望された数学者でプリンストン大から招請を受けたが、その直後の1958年11月、謎の自殺を遂げている。
数学という一見、無味乾燥な世界にも実に多くのドラマがある。望月教授のABC予想の解決がいつ公式のものになるか見当がつかないが、その瞬間は数千年におよぶ人類の数学史をいろどる栄光の一場面となることは間違いない。本書は、数学に関心のある人もない人も、すっかり休眠した「数学脳」を活性化させる、またとないチャンスになるはずだ。
加藤教授の最後の本音が印象的だった。「ここまで書いてきてみて、改めて、やはりIUT理論というのは、難しい理論だなと感じます。専門家でない人にも、できるだけ、その基本思想がわかるように、というのがこの本の目標の一つでしたが、まぁ、このあたりが限界かなと思います」「技術的には難しい理論ですが、少なくともそれが意図するものは、珍奇な概念の複雑怪奇なからまり合いなどではなく、我々普通の人間が普通に理解できるような自然な考え方や発想に根差しているわけです。だからこそ、それは『凄い理論』なのだと思います」。









