ジュニア数学オリンピックの簡単な問題（１２１）

こんにちは。東久留米市の学習塾塾長です。

昨夜から雨が降ったり止んだりのパッとしない天気で、最高気温も１０℃と寒い日になりました。明日もぐずついた空模様で、気温はさらに下がりますが、明後日は暖かく過ごしやすい日になるようです。

さて、今回は２０１７年ジュニア数学オリンピック予選に出題された場合の数の問題を取り上げます。

問題は、
「下図のような２×７のマス目の各マスに、１以上１４以下の相異なる整数を１つずつ書き込む。次の条件をみたすような書き込み方は何通りあるか。

　●それぞれの行について、書かれている７個の整数は左から小さい順に並んでいる。
　●１以上６以下のすべての整数ｋについて、左からｋ＋１番目の列に書かれた２つの数の差は、ｋ番目の列に書かれた２つの数の差以上である。」

▲問題図

早速、取り掛かりましょう。

１つ目の条件から１４はマス目の右端のマスに書かれます。

さらに、右端に書かれた２つの数の差がｎ（１≦ｎ≦７）のとき、右端の列には１４と１４－ｎが書き込まれ、１４と１４－ｎの間にあるｎ個の数は大きい順に１４の隣に書き並べることになるので、右端からｎ列目までに書かれる数は決まってしまいます。

これらに注意して、右端の列に書かれた２つの数の差で場合分けして調べていきましょう。

●図１のように、右端の列に書かれた２つの数の差が１の場合です。

▲図１．右端の列に書かれた２つの数の差が１の場合

・空いている６列に書き込まれる２つの数の差は１ですから、順に、（１２，１１）、（１０，９）、（８，７）、（６，５）、（４，３）、（２，１）書き込むことになり、これらの２つの数は上下のどちらの行でも書き込むことができるので、この場合の書き込み方は
（１４，１３の書き込み方）×２^6＝２×２^6＝１２８通り
です。

●図２のように、右端の列に書かれた２つの数の差が２の場合です。

▲図２．右端の列に書かれた２つの数の差が２の場合

・空いている５列に書き込まれる２つの数の差が１になる書き込み方は、
（１４，１３，１２，１１の書き込み方）×２^5＝２×２^5＝６４通り
です。

・右から３、４番目の列に書かれた２つの数の差が２で、それより左の列に書かれた２つの数の差が１になる書き込み方は、
（１４，１３，１２，１１の書き込み方）×（１０，９，８，７の書き込み方）×２^3＝２×２×２^3＝３２通り
です。

・右から３、４番目と５、６番目の列に書かれた２つの数の差が２で、それより左の列に書かれた２つの数の差が１になる書き込み方は、
（１４，１３，１２，１１の書き込み方）×（１０，９，８，７の書き込み方）×（６，５，４，３の書き込み方）×２＝２×２×２×２＝１６通り
です。

●図３のように、右端の列に書かれた２つの数の差が３の場合です。

▲図３．右端の列に書かれた２つの数の差が３の場合

・空いている４列に書き込まれる２つの数の差が１になる書き込み方は、
（１４，１３，１２，１１，１０，９の書き込み方）×２^4＝２×２^4＝３２通り
です。

・右から４、５、６番目の列に書かれた２つの数の差が３で、それより左の列に書かれた２つの数の差が１になる書き込み方は、
（１４，１３，１２，１１，１０，９の書き込み方）×（８，７，６，５，４，３の書き込み方）×２＝２×２×２＝８通り
です。

・右から４、５番目の列に書かれた２つの数の差が２で、それより左の列に書かれた２つの数の差が１になる書き込み方は、
（１４，１３，１２，１１，１０，９の書き込み方）×（８，７，６，５の書き込み方）×２^2＝２×２×２^2＝１６通り
です。

・右から４、５番目と６、７番目の列に書かれた２つの数の差が２になる書き込み方は、
（１４，１３，１２，１１，１０，９の書き込み方）×（８，７，６，５の書き込み方）×（４，３，２，１の書き込み方）＝２×２×２＝８通り
です。

●図４のように、右端の列に書かれた２つの数の差が４の場合です。

▲図４．右端の列に書かれた２つの数の差が４の場合

・空いている３列に書き込まれる２つの数の差が１になる書き込み方は、
（１４，１３，１２，１１，１０，９，８，７の書き込み方）×２^3＝２×２^3＝１６通り
です。

・右から５、６，７番目の列に書かれた２つの数の差が３になる書き込み方は、
（１４，１３，１２，１１，１０，９，８，７の書き込み方）×（６，５，４，３，２，１の書き込み方）＝２×２＝４通り
です。

・右から５、６番目の列に書かれた２つの数の差が２で、それより左の列に書かれた２つの数の差が１になる書き込み方は、
（１４，１３，１２，１１，１０，９，８，７の書き込み方）×（６，５，４，３の書き込み方）×２＝２×２×２＝８通り
です。

●図５のように、右端の列に書かれた２つの数の差が５の場合です。

▲図５．右端の列に書かれた２つの数の差が５の場合

・空いている２列に書き込まれる２つの数の差が１になる書き込み方は、
（１４，１３，１２，１１，１０，９，８，７、６，５の書き込み方）×２^2＝２×２^2＝８通り
です。

・右から６，７番目の列に書かれた２つの数の差が２になる書き込み方は、
（１４，１３，１２，１１，１０，９，８，７，６，５の書き込み方）×（４，３，２，１の書き込み方）＝２×２＝４通り
です。

●図６のように、右端の列に書かれた２つの数の差が６の場合です。

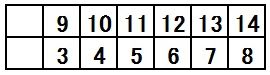
▲図６．右端の列に書かれた２つの数の差が６の場合

・空いている１列に書き込まれる２つの数の差が１になる書き込み方は、
（１４，１３，１２，１１，１０，９，８，７、６，５，４，３の書き込み方）×２＝２×２＝４通り
です。

●図７のように、右端の列に書かれた２つの数の差が７の場合です。

▲図７．右端の列に書かれた２つの数の差が７の場合

・（１４，１３，１２，１１，１０，９，８，７、６，５，４，３，２，１の書き込み方）＝２通り
です。

以上から、問題に与えられた２つの条件をみたす書き込み方は、
１２８＋６４＋３２＋１６＋３２＋８＋１６＋８＋１６＋４＋８＋８＋４＋４＋２＝３５０通り
で、これが答えです。


楽しい問題です。