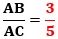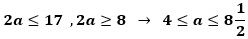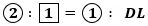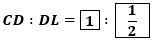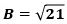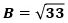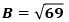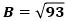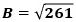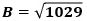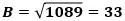こんにちは。東久留米市の学習塾塾長です。
今回は、令和2年度開成入試問題です。
問題は、
「AB=AC=AD=6、BC=BD=CD=4 である四面体ABCDがある。辺ABの中点をPとし、辺AC、AD上にそれぞれ点Q、RをAQ>ARとなるようにとる。このとき、次の問いに答えよ。

(1) △ABCの面積を求めよ。
(2) 辺AC上の点Hを∠PHA=90°となるようにとるとき、線分AHの長さを求めよ。
(3) AQ=4、PQ=PR のとき、線分ARの長さを求めよ。
(4) △PQRが二等辺三角形であり、四面体APQRの体積が四面体ABCDの体積の
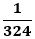
となるような線分AQ、ARの長さの組をすべて求めよ。ただし、解答欄はすべて使うとは限らない。」
です。
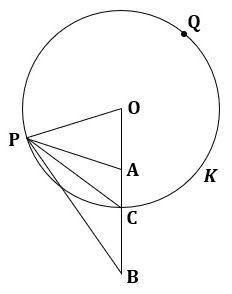
図1に、与えられた条件を書き入れました。
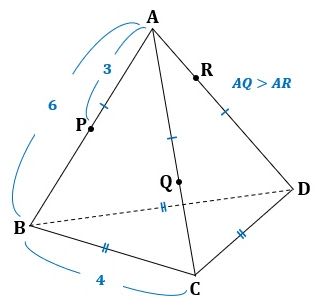
▲図1.与えられた条件を書き入れました
初めに、△ABCの面積です。
図2のように、Aから辺BCに垂線を下ろし、その足をEとすると、BE=2になります。
ここで、△ABEに三平方の定理を適用すると、

が成り立ち、これに、BE=2、AB=6を代入し整理すると、

で、AE>0から

です。
したがって、△ABCの面積は、
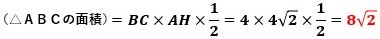
で、これが(1)の答えです。
次に(2)です。
図2のように、Bから辺ACに垂線を下ろし、その足をFとすると、PH//BFになり、AP=PBからAH=HFが成り立ちます。
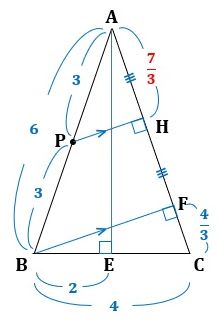
▲図2.Bから辺ACに垂線を下ろし、その足をFとしました
一方、∠AEB=∠BFC=90°、∠ABE=∠ABC=∠ACB=∠ECFから、△ABE∽△BCFになります。
すると、AB:BE=BC:CFが成り立ち、これに、AB=6、BE=2、BC=4を代入し整理すると、

になり、したがって、

で、これが答えです。
次に(3)です。
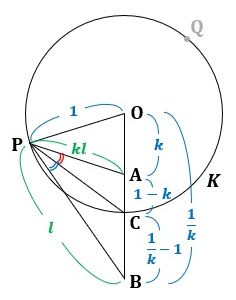
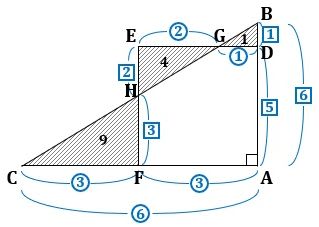
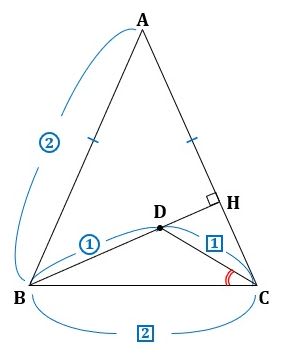
△ABC≡△ABDなので、△ABCと△ABDを重ねて図3の右側の図を調べます。

▲図3.△ABCと△ABDを重ねました
ここで、△PQRは二等辺三角形なので、QH=RHです。
すると、
AR=2AH-AQ
になり、これに、

を代入して、

で、これが答えです。
(4)は次回です。
今回は、令和2年度開成入試問題です。
問題は、
「AB=AC=AD=6、BC=BD=CD=4 である四面体ABCDがある。辺ABの中点をPとし、辺AC、AD上にそれぞれ点Q、RをAQ>ARとなるようにとる。このとき、次の問いに答えよ。

(1) △ABCの面積を求めよ。
(2) 辺AC上の点Hを∠PHA=90°となるようにとるとき、線分AHの長さを求めよ。
(3) AQ=4、PQ=PR のとき、線分ARの長さを求めよ。
(4) △PQRが二等辺三角形であり、四面体APQRの体積が四面体ABCDの体積の
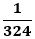
となるような線分AQ、ARの長さの組をすべて求めよ。ただし、解答欄はすべて使うとは限らない。」
です。
図1に、与えられた条件を書き入れました。

▲図1.与えられた条件を書き入れました
初めに、△ABCの面積です。
図2のように、Aから辺BCに垂線を下ろし、その足をEとすると、BE=2になります。
ここで、△ABEに三平方の定理を適用すると、

が成り立ち、これに、BE=2、AB=6を代入し整理すると、

で、AE>0から

です。
したがって、△ABCの面積は、
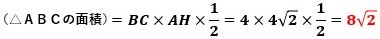
で、これが(1)の答えです。
次に(2)です。
図2のように、Bから辺ACに垂線を下ろし、その足をFとすると、PH//BFになり、AP=PBからAH=HFが成り立ちます。

▲図2.Bから辺ACに垂線を下ろし、その足をFとしました
一方、∠AEB=∠BFC=90°、∠ABE=∠ABC=∠ACB=∠ECFから、△ABE∽△BCFになります。
すると、AB:BE=BC:CFが成り立ち、これに、AB=6、BE=2、BC=4を代入し整理すると、

になり、したがって、

で、これが答えです。
次に(3)です。
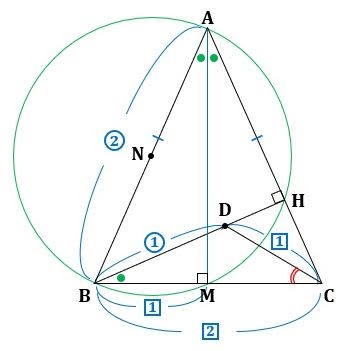
△ABC≡△ABDなので、△ABCと△ABDを重ねて図3の右側の図を調べます。

▲図3.△ABCと△ABDを重ねました
ここで、△PQRは二等辺三角形なので、QH=RHです。
すると、
AR=2AH-AQ
になり、これに、

を代入して、

で、これが答えです。
(4)は次回です。