こんにちは。東久留米市の学習塾塾長です。
今回は、2018年日本数学オリンピック予選に出題された図形問題を取り上げます。
問題は、
「三角形ABCの内接円が辺BC、CA、ABとそれぞれ点P、Q、Rで、∠A内の傍接円が辺BC、直線CA,ABとそれぞれ点S、T、Uで接している。三角形ABCの内心を I 、直線PQと直線STの交点をD、直線PRと直線SUの交点をEとする。AI=3、IP=1、PS=2のとき、線分DEの長さを求めよ。
ただし、XYで線分XYの長さを表すものとする。また、三角形ABCの∠A内の傍接円とは、辺BC、辺ABの点B側への延長線、および辺ACの点C側への延長線に接する円のことをさす。」
です。
早速図1のように、問題の図を描きましょう。
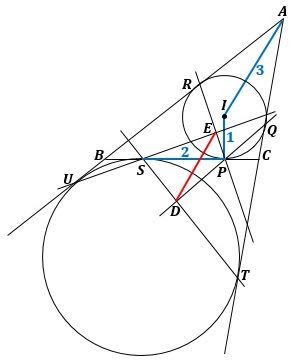
▲図1.問題の図を描きました
図1を眺めると、多くの二等辺三角形や平行線、直交する直線が目につくので、角度に注目して進めてみましょう。
そこで図2のように、A、B、Cと I をそれぞれ結び、1/2∠A=●、1/2∠B=●、1/2∠C=●とします。

▲図2.1/2∠A=●、1/2∠B=●、1/2∠C=●としました
まず、1/2∠B=●を調べていきましょう。
図3のように、∠ABC=∠BUS+∠BSUで、さらに△BUSは二等辺三角形で∠BUS=∠BSUですから、∠BUS=∠BSU=●です。
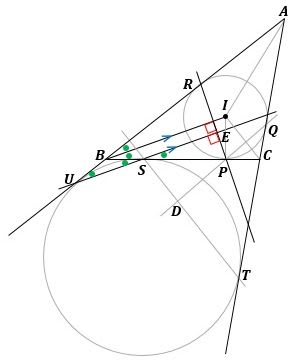
▲図3.1/2∠B=●を調べていきます
すると、∠ABI=∠BUS=∠BUEですから、BI//UEです。
一方、△BPRは二等辺三角形で、∠Bの二等分線BIはPRと直交するので、BI//UEから∠SEP=90°です。
また、対頂角は等しいので、∠BSU=∠PSEが成り立ちます。
同様に、1/2∠C=●を調べていきましょう。
図4のように、∠ACB==∠CTS+∠CSTで、さらに△CTSは二等辺三角形で∠CTS=∠CSTですから、∠CTS=∠CST=●です。

▲図4.1/2∠C=●を調べていきます
すると、∠ACI=∠ATSですから、CI//TSです。
一方、△CPQは二等辺三角形で、∠Cの二等分線CIはPQと直交するので、CI//TSから∠PDS=90°です。
ここまでで、四角形PDSEについていろいろなことが判りました。
まず、対角(∠SEPと∠PDS)がそれぞれ90°なので、四角形PDSEは円に内接し、その直径(PS)は2です。
さらに、一つの内角DSEの大きさは、●+●です。
そこで、●+●となる角を探してみると、図5のように、∠AIQ=●+●であることが容易に見つかります。

▲図5.∠AIQ=●+●です
ここで△AIQに三平方の定理を適用すると、AI=3、IQ=IP=1ですから、AQ=2√2です。
一方、図6のように、四角形PDSEに注目し、Dと内接円の中心を通る直線と内接円の交点でDでない方をFとすると、∠DSEと∠DFEは円弧DPEに対する円周角なので、∠DSE=∠DFE=●+●です。

▲図6.四角形PDSEに注目します
すると、△DEF∽△AQIで、DF=2ですから、DE=DF×AQ/AI=2×2√2/3= 4√2/3 で、これが答えです。
楽しい問題です。
今回は、2018年日本数学オリンピック予選に出題された図形問題を取り上げます。
問題は、
「三角形ABCの内接円が辺BC、CA、ABとそれぞれ点P、Q、Rで、∠A内の傍接円が辺BC、直線CA,ABとそれぞれ点S、T、Uで接している。三角形ABCの内心を I 、直線PQと直線STの交点をD、直線PRと直線SUの交点をEとする。AI=3、IP=1、PS=2のとき、線分DEの長さを求めよ。
ただし、XYで線分XYの長さを表すものとする。また、三角形ABCの∠A内の傍接円とは、辺BC、辺ABの点B側への延長線、および辺ACの点C側への延長線に接する円のことをさす。」
です。
早速図1のように、問題の図を描きましょう。

▲図1.問題の図を描きました
図1を眺めると、多くの二等辺三角形や平行線、直交する直線が目につくので、角度に注目して進めてみましょう。
そこで図2のように、A、B、Cと I をそれぞれ結び、1/2∠A=●、1/2∠B=●、1/2∠C=●とします。

▲図2.1/2∠A=●、1/2∠B=●、1/2∠C=●としました
まず、1/2∠B=●を調べていきましょう。
図3のように、∠ABC=∠BUS+∠BSUで、さらに△BUSは二等辺三角形で∠BUS=∠BSUですから、∠BUS=∠BSU=●です。

▲図3.1/2∠B=●を調べていきます
すると、∠ABI=∠BUS=∠BUEですから、BI//UEです。
一方、△BPRは二等辺三角形で、∠Bの二等分線BIはPRと直交するので、BI//UEから∠SEP=90°です。
また、対頂角は等しいので、∠BSU=∠PSEが成り立ちます。
同様に、1/2∠C=●を調べていきましょう。
図4のように、∠ACB==∠CTS+∠CSTで、さらに△CTSは二等辺三角形で∠CTS=∠CSTですから、∠CTS=∠CST=●です。

▲図4.1/2∠C=●を調べていきます
すると、∠ACI=∠ATSですから、CI//TSです。
一方、△CPQは二等辺三角形で、∠Cの二等分線CIはPQと直交するので、CI//TSから∠PDS=90°です。
ここまでで、四角形PDSEについていろいろなことが判りました。
まず、対角(∠SEPと∠PDS)がそれぞれ90°なので、四角形PDSEは円に内接し、その直径(PS)は2です。
さらに、一つの内角DSEの大きさは、●+●です。
そこで、●+●となる角を探してみると、図5のように、∠AIQ=●+●であることが容易に見つかります。

▲図5.∠AIQ=●+●です
ここで△AIQに三平方の定理を適用すると、AI=3、IQ=IP=1ですから、AQ=2√2です。
一方、図6のように、四角形PDSEに注目し、Dと内接円の中心を通る直線と内接円の交点でDでない方をFとすると、∠DSEと∠DFEは円弧DPEに対する円周角なので、∠DSE=∠DFE=●+●です。

▲図6.四角形PDSEに注目します
すると、△DEF∽△AQIで、DF=2ですから、DE=DF×AQ/AI=2×2√2/3= 4√2/3 で、これが答えです。
楽しい問題です。




















