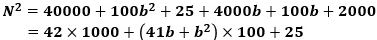こんにちは。東久留米市の学習塾塾長です。
今回は、2019年日本数学オリンピック予選に出題された整数問題を取り上げます。
問題は、
「97、100、103で割った余りがそれぞれ32、33、34である正の整数のうち最小のものを求めよ。」
です。
早速、取り掛かりましょう。
97、100、103で割った余りがそれぞれ32、33、34である正の整数をNとし、Nを97、100、103で割ったときの商をそれぞれQ1、Q2、Q3 とすると、
N÷ 97=Q1・・・32
N÷100=Q2・・・33
N÷103=Q3・・・34
が成り立ちます。
これらを変形すると、
N= 97Q1+32 (1)
N=100Q2+33 (2)
N=103Q3+34 (3)
になります。
あとは、(1)(2)(3)の整数解を求めて、最小の正の整数N’を計算するだけです。
まず(1)と(2)から
97Q1+32=100Q2+33
が成り立ち、これを整理して、
97Q1-100Q2=1 (4)
としましょう。
ここで(4)を満たす整数q1、q2を見つけるために、
97q1-(97+3)q2=1
97(q1-q2)-3q2=1
(32×3+1)(q1-q2)-3q2=1
3{32(q1-q2)-q2}+(q1-q2)=1 (5)
と変形すると、(5)を満たす32(q1-q2)-q2 とq1-q2 は容易に見つけることができて、そのなかの一つは、
32(q1-q2)-q2=0
q1-q2=1
で、これらから、
q1=33
q2=32
になります。
続いて、これらを(4)に代入して、
97×33-100×32=1
とし、(4)の辺々から引くと、
97(Q1-33)-100(Q2-32)=0
97(Q1-33)=100(Q2-32) (6)
が成り立ちます。
(6)で、97と100は互いに素なので、
Q2-32=97m
Q2=97m+32 (mは整数) (7)
と表すことができます。
次に(2)と(3)で同じ作業をします。
(2)と(3)から
100Q2+33=103Q3+34
が成り立ち、これを整理して、
100Q2-103Q3=1 (8)
とします。
ここで(8)を満たす整数q2、q3を見つけるために、
100q2-(100+3)q3=1
100(q2-q3)-3q3=1
(33×3+1)(q2-q3)-3q3=1
3{33(q2-q3)-q3}+(q2-q3)=1 (9)
と変形すると、(9)を満たす33(q2-q3)-q3 とq2-q3 は容易に見つけることができて、そのなかの一つは、
33(q2-q3)-q3=0
q2-q3=1
で、これらから、
q2=34
q3=33
になります。
続いて、これらを(6)に代入して、
100×34-103×33=1
とし、(6)の辺々から引くと、
100(Q2-34)-103(Q3-33)=0
100(Q2-34)=103(Q3-33) (10)
が成り立ちます。
(10)で、100と103は互いに素なので、
Q2-34=103n
Q2=103n+34 (nは整数) (11)
と表すことができます。
あとは(7)と(11)からmを求めましょう。
(7)と(11)から
97m+32=103n+34
が成り立ち、これを整理して、
97m-103n=2 (12)
とします。
ここで(12)を満たす整数m’、n’を見つけるために、
97m’-103n’=2
97m’-(97+6)n’=2
97(m’-n’)-6n’=2
(16×6+1)(m’-n’)-6n’=2
6{16(m’-n’)-n’}+(m’-n’)=2 (13)
と変形すると、(13)を満たす16(m’-n’)-n’、m’-n’は容易に見つけることができて、そのなかの一つは、
16(m’-n’)-n’=0
m’-n’=2
で、これから、
m’=34
n’=32
になります。
続いて、これらを(12)に代入して、
97×34-103×32=2
とし、(12)の辺々から引くと、
97(m-34)-103(n-32)=0
97(m-34)=103(n-32) (14)
が成り立ちます。
(14)で、97と103は互いに素なので、
m-34=103k
m=103k+34 (kは整数) (15)
と表すことができます。
ここで、Nが最小の正の整数N’になるのは、(2)からQ2が最小の非負整数になるとき、つまり(7)からmが最小の非負整数になるときで、したがって、(15)からk=0で、このとき、m=34です。
したがって、(7)から
Q2=97×34+32=3330
で、(2)から
N’=100×3330+33= 333033
で、これが答えです。
ここでは、不定方程式を解く作業を3回行いましたが、N=100A+33とし、100A+1と100A-1がそれぞれ97と103で割りきれることを利用すると、不定方程式を解く作業が1回になります。
今回は、2019年日本数学オリンピック予選に出題された整数問題を取り上げます。
問題は、
「97、100、103で割った余りがそれぞれ32、33、34である正の整数のうち最小のものを求めよ。」
です。
早速、取り掛かりましょう。
97、100、103で割った余りがそれぞれ32、33、34である正の整数をNとし、Nを97、100、103で割ったときの商をそれぞれQ1、Q2、Q3 とすると、
N÷ 97=Q1・・・32
N÷100=Q2・・・33
N÷103=Q3・・・34
が成り立ちます。
これらを変形すると、
N= 97Q1+32 (1)
N=100Q2+33 (2)
N=103Q3+34 (3)
になります。
あとは、(1)(2)(3)の整数解を求めて、最小の正の整数N’を計算するだけです。
まず(1)と(2)から
97Q1+32=100Q2+33
が成り立ち、これを整理して、
97Q1-100Q2=1 (4)
としましょう。
ここで(4)を満たす整数q1、q2を見つけるために、
97q1-(97+3)q2=1
97(q1-q2)-3q2=1
(32×3+1)(q1-q2)-3q2=1
3{32(q1-q2)-q2}+(q1-q2)=1 (5)
と変形すると、(5)を満たす32(q1-q2)-q2 とq1-q2 は容易に見つけることができて、そのなかの一つは、
32(q1-q2)-q2=0
q1-q2=1
で、これらから、
q1=33
q2=32
になります。
続いて、これらを(4)に代入して、
97×33-100×32=1
とし、(4)の辺々から引くと、
97(Q1-33)-100(Q2-32)=0
97(Q1-33)=100(Q2-32) (6)
が成り立ちます。
(6)で、97と100は互いに素なので、
Q2-32=97m
Q2=97m+32 (mは整数) (7)
と表すことができます。
次に(2)と(3)で同じ作業をします。
(2)と(3)から
100Q2+33=103Q3+34
が成り立ち、これを整理して、
100Q2-103Q3=1 (8)
とします。
ここで(8)を満たす整数q2、q3を見つけるために、
100q2-(100+3)q3=1
100(q2-q3)-3q3=1
(33×3+1)(q2-q3)-3q3=1
3{33(q2-q3)-q3}+(q2-q3)=1 (9)
と変形すると、(9)を満たす33(q2-q3)-q3 とq2-q3 は容易に見つけることができて、そのなかの一つは、
33(q2-q3)-q3=0
q2-q3=1
で、これらから、
q2=34
q3=33
になります。
続いて、これらを(6)に代入して、
100×34-103×33=1
とし、(6)の辺々から引くと、
100(Q2-34)-103(Q3-33)=0
100(Q2-34)=103(Q3-33) (10)
が成り立ちます。
(10)で、100と103は互いに素なので、
Q2-34=103n
Q2=103n+34 (nは整数) (11)
と表すことができます。
あとは(7)と(11)からmを求めましょう。
(7)と(11)から
97m+32=103n+34
が成り立ち、これを整理して、
97m-103n=2 (12)
とします。
ここで(12)を満たす整数m’、n’を見つけるために、
97m’-103n’=2
97m’-(97+6)n’=2
97(m’-n’)-6n’=2
(16×6+1)(m’-n’)-6n’=2
6{16(m’-n’)-n’}+(m’-n’)=2 (13)
と変形すると、(13)を満たす16(m’-n’)-n’、m’-n’は容易に見つけることができて、そのなかの一つは、
16(m’-n’)-n’=0
m’-n’=2
で、これから、
m’=34
n’=32
になります。
続いて、これらを(12)に代入して、
97×34-103×32=2
とし、(12)の辺々から引くと、
97(m-34)-103(n-32)=0
97(m-34)=103(n-32) (14)
が成り立ちます。
(14)で、97と103は互いに素なので、
m-34=103k
m=103k+34 (kは整数) (15)
と表すことができます。
ここで、Nが最小の正の整数N’になるのは、(2)からQ2が最小の非負整数になるとき、つまり(7)からmが最小の非負整数になるときで、したがって、(15)からk=0で、このとき、m=34です。
したがって、(7)から
Q2=97×34+32=3330
で、(2)から
N’=100×3330+33= 333033
で、これが答えです。
ここでは、不定方程式を解く作業を3回行いましたが、N=100A+33とし、100A+1と100A-1がそれぞれ97と103で割りきれることを利用すると、不定方程式を解く作業が1回になります。