こんにちは。東久留米市の学習塾塾長です。
今回は、2021年日本数学オリンピック予選の問題です。
問題は、
「黒板に3つの相異なる正の整数が書かれている。黒板に実数a、b、cが書かれているとき、それぞれを

に同時に書き換えるという操作を考える。この操作を2021回行ったところ、最後に黒板に書かれた3つの数はすべて正の整数だった。このとき、最初に書かれていた3つの正の整数の和としてありうる最小の値を求めよ。」
です。
最初に書かれていた3つの相異なる正の整数を a0、b0、c0 とします。このとき、対称性から 1≦a0<b0<c0 としても一般性は失いません。
また、1以上2021以下の整数nについて、n回目の操作後に黒板に書かれている数をan、bn、cn とすると、
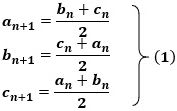
が成り立ち、これらの式の辺々を足し合わせると、

になり、したがって、

で、これらから、
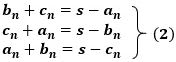
になります。ここで、最初に書かれていた3つの正の整数の和をsとしました。
続いて(2)を(1)に代入すると、
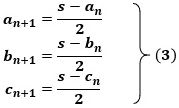
になり、これらの漸化式を解くと、

です。
ここで(4)から bn-an、cn-an をつくり、さらにn=2021とすると、
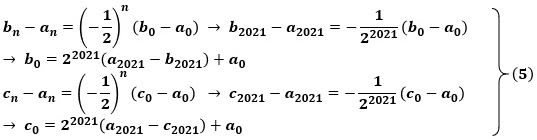
で、これらから、
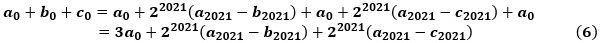
になります。
一方(5)から、

になり、このとき a2021、b2021 はともに整数なので、

です。
さらに(5)から

になり、このとき a2021、c2021 はともに整数なので、

です。
すると、a≧1 、(6)(7)(8)から、
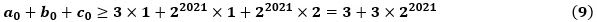
が成り立ちます。
ここから、

のとき、(6)の不等式の等号が成り立ち、かつ、a2021、b2021、c2021 が正の整数になるかを調べます。

なので、(6)の不等式の等号は成り立ちます。
また(4)から、
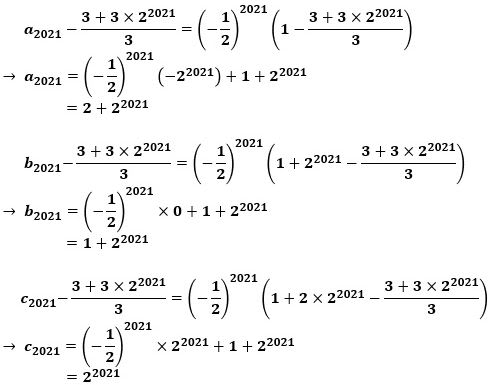
で、a2021、b2021、c2021 は正の整数になり、与えられた条件を満たします。
以上から、最初に書かれていた3つの正の整数の和としてありうる最小の値は、

で、これが答えです。
簡単な問題です。
今回は、2021年日本数学オリンピック予選の問題です。
問題は、
「黒板に3つの相異なる正の整数が書かれている。黒板に実数a、b、cが書かれているとき、それぞれを

に同時に書き換えるという操作を考える。この操作を2021回行ったところ、最後に黒板に書かれた3つの数はすべて正の整数だった。このとき、最初に書かれていた3つの正の整数の和としてありうる最小の値を求めよ。」
です。
最初に書かれていた3つの相異なる正の整数を a0、b0、c0 とします。このとき、対称性から 1≦a0<b0<c0 としても一般性は失いません。
また、1以上2021以下の整数nについて、n回目の操作後に黒板に書かれている数をan、bn、cn とすると、
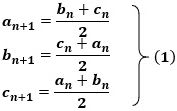
が成り立ち、これらの式の辺々を足し合わせると、

になり、したがって、

で、これらから、
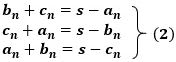
になります。ここで、最初に書かれていた3つの正の整数の和をsとしました。
続いて(2)を(1)に代入すると、
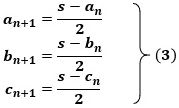
になり、これらの漸化式を解くと、

です。
ここで(4)から bn-an、cn-an をつくり、さらにn=2021とすると、
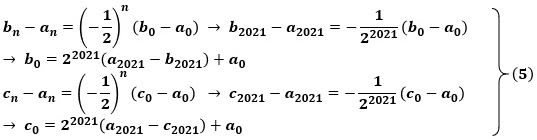
で、これらから、
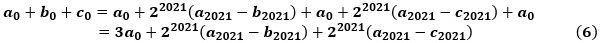
になります。
一方(5)から、

になり、このとき a2021、b2021 はともに整数なので、

です。
さらに(5)から

になり、このとき a2021、c2021 はともに整数なので、

です。
すると、a≧1 、(6)(7)(8)から、
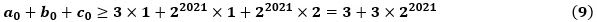
が成り立ちます。
ここから、

のとき、(6)の不等式の等号が成り立ち、かつ、a2021、b2021、c2021 が正の整数になるかを調べます。

なので、(6)の不等式の等号は成り立ちます。
また(4)から、
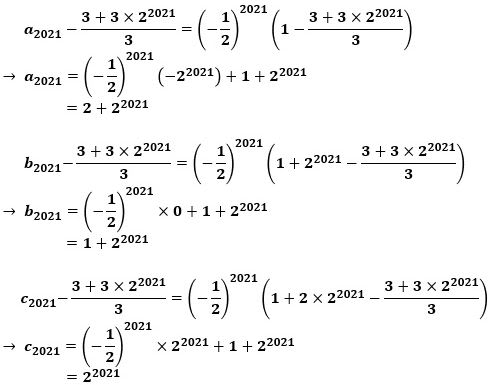
で、a2021、b2021、c2021 は正の整数になり、与えられた条件を満たします。
以上から、最初に書かれていた3つの正の整数の和としてありうる最小の値は、

で、これが答えです。
簡単な問題です。




















