こんにちは。東久留米市の学習塾塾長です。
今回は平成30年度都立高校数学入試問題を取り上げます。
問題は、国立高で出題された大問4の図形問題で、それは、
「下の図1に示した立体C-APBは、AB=4cm、BC=2cm、∠CBA=∠CBP=90°の三角すいである。

▲図1.問題図(1)
ただし、点Pは2点A、Bを直径とする半円の弧AB上にある点で、点Aと点Bのいずれにも一致しない。
次の各問に答えよ。
[問1] △CPBの面積が△CABの面積の1/2となるとき、三角すいC-APBの体積は何cm3か。
[問2] 点Bから平面CAPに垂直な直線を引き、その交点をHとした場合を考える。
三角すいC-APBの体積が最も大きくなるとき、線分BHの長さは何cmか。
ただし、答えだけでなく答えを求める過程が分かるように、途中の式や説明なども書け。
[問3] 下の図2は、図1において、弧AP:弧PB=2:1、弧AP上にあり弧AQ:弧QP=1:1である点をQ、辺BCの中点をMとし、点Qと点Mを結び、線分QMと平面CAPの交点をRとした場合を表している。
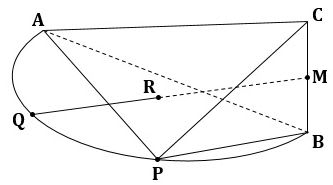
▲図2.問題図(2)
点Rと点A、点Rと点P、点Rと点Bをそれぞれ結んでできる三角すいR-APBの体積は何cm3か。」
です。
△CABの面積は 4×2×1/2=4cm2 ですから、△CPBの面積は 2cm2 で、したがって、図3のように、PB=2cmになります。
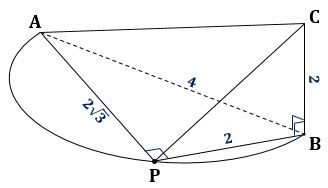
▲図3.PB=2cmです
また、点Pは線分ABを直径とする半円周上の点なので、∠APB=90°です。
そこで、直角三角形ABPに三平方の定理を適用すると、

が成り立ち、ここに AB=4cm、BP=2cmを代入すると、
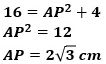
です。
すると、△ABPの面積は、
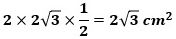
になり、三角すいC-APBの体積は、

で、これが[問1]の答えです。
次に[問2]です。
三角すいC-APBの体積が最も大きくなるのは△APBの面積が最大になるときで、それは図4のように、点Pが、∠AOP=90°となる位置にあるときです。
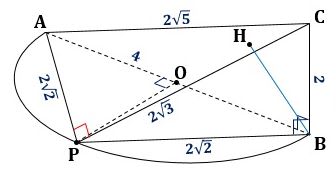
▲図4.∠AOP=90°のとき、三角すいC-APBの体積が最大になります
このとき、△APBは直角二等辺三角形なので、
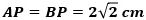
で、その面積は4cm2になります。
したがって、三角すいC-APBの体積は、4×2×1/3=8/3 cm3 になります。
続いて△APCの面積を計算しましょう。
図4のように、直角三角形ABC、PBCに三平方の定理を適用して、

を求め、それらを二乗すると
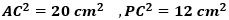
になります。
このとき
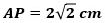
から
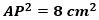
なので、
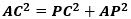
が成り立ち、三平方の定理の逆から∠APC=90°です。
したがって、△APCの面積は、

になります。
ここで、三角すいC-APBの底面を△APCとすると、その体積は、
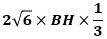
で、これが8/3になることから

で、これが答えです。
最後の[問3]です。
図5のように、点PとQは、弧AQ=弧QP=弧PBを満たす位置になります。

▲図5.弧AQ=弧QP=弧PBになります
すると、△APBと△AQBはその内角が90°、60°、30°の直角三角形になり、

なので、△APBの面積は、
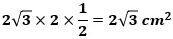
です。
また、直線APと直線BQとの交点をSとすると、△OBSはその内角が90°、60°、30°の直角三角形で、

になります。
ここで図6のように、平面BCQを考えると、直線CSと直線MQとの交点がRになり、RTを求めれば三角すいR-APBの体積を計算することができます。
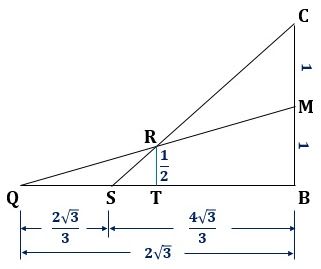
▲図6.平面BCQを考えます
△QRT∽△QMBから、QT:RT=QB:MBなので、
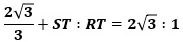
で、これを整理して、
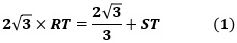
です。
△SRT∽△SCBから、ST:RT=SB:CBなので、
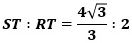
で、これを整理して、
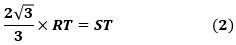
です。
(1)と(2)から、
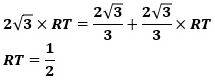
です。
したがって、三角すいR-APBの体積は、

で、これが答えです。
簡単な問題です。
今回は平成30年度都立高校数学入試問題を取り上げます。
問題は、国立高で出題された大問4の図形問題で、それは、
「下の図1に示した立体C-APBは、AB=4cm、BC=2cm、∠CBA=∠CBP=90°の三角すいである。

▲図1.問題図(1)
ただし、点Pは2点A、Bを直径とする半円の弧AB上にある点で、点Aと点Bのいずれにも一致しない。
次の各問に答えよ。
[問1] △CPBの面積が△CABの面積の1/2となるとき、三角すいC-APBの体積は何cm3か。
[問2] 点Bから平面CAPに垂直な直線を引き、その交点をHとした場合を考える。
三角すいC-APBの体積が最も大きくなるとき、線分BHの長さは何cmか。
ただし、答えだけでなく答えを求める過程が分かるように、途中の式や説明なども書け。
[問3] 下の図2は、図1において、弧AP:弧PB=2:1、弧AP上にあり弧AQ:弧QP=1:1である点をQ、辺BCの中点をMとし、点Qと点Mを結び、線分QMと平面CAPの交点をRとした場合を表している。

▲図2.問題図(2)
点Rと点A、点Rと点P、点Rと点Bをそれぞれ結んでできる三角すいR-APBの体積は何cm3か。」
です。
△CABの面積は 4×2×1/2=4cm2 ですから、△CPBの面積は 2cm2 で、したがって、図3のように、PB=2cmになります。

▲図3.PB=2cmです
また、点Pは線分ABを直径とする半円周上の点なので、∠APB=90°です。
そこで、直角三角形ABPに三平方の定理を適用すると、

が成り立ち、ここに AB=4cm、BP=2cmを代入すると、
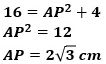
です。
すると、△ABPの面積は、
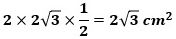
になり、三角すいC-APBの体積は、

で、これが[問1]の答えです。
次に[問2]です。
三角すいC-APBの体積が最も大きくなるのは△APBの面積が最大になるときで、それは図4のように、点Pが、∠AOP=90°となる位置にあるときです。

▲図4.∠AOP=90°のとき、三角すいC-APBの体積が最大になります
このとき、△APBは直角二等辺三角形なので、
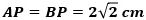
で、その面積は4cm2になります。
したがって、三角すいC-APBの体積は、4×2×1/3=8/3 cm3 になります。
続いて△APCの面積を計算しましょう。
図4のように、直角三角形ABC、PBCに三平方の定理を適用して、

を求め、それらを二乗すると
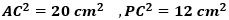
になります。
このとき
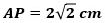
から
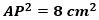
なので、
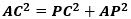
が成り立ち、三平方の定理の逆から∠APC=90°です。
したがって、△APCの面積は、

になります。
ここで、三角すいC-APBの底面を△APCとすると、その体積は、
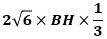
で、これが8/3になることから

で、これが答えです。
最後の[問3]です。
図5のように、点PとQは、弧AQ=弧QP=弧PBを満たす位置になります。

▲図5.弧AQ=弧QP=弧PBになります
すると、△APBと△AQBはその内角が90°、60°、30°の直角三角形になり、

なので、△APBの面積は、
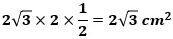
です。
また、直線APと直線BQとの交点をSとすると、△OBSはその内角が90°、60°、30°の直角三角形で、

になります。
ここで図6のように、平面BCQを考えると、直線CSと直線MQとの交点がRになり、RTを求めれば三角すいR-APBの体積を計算することができます。

▲図6.平面BCQを考えます
△QRT∽△QMBから、QT:RT=QB:MBなので、
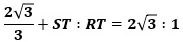
で、これを整理して、
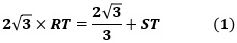
です。
△SRT∽△SCBから、ST:RT=SB:CBなので、
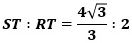
で、これを整理して、
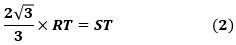
です。
(1)と(2)から、
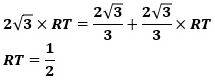
です。
したがって、三角すいR-APBの体積は、

で、これが答えです。
簡単な問題です。




















