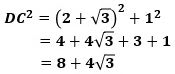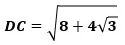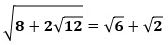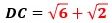こんにちは。東久留米市の学習塾塾長です。
東西に長くのびた前線を伴う南岸低気圧の影響で、気温がぐっと下がりました。さらに明日も下がって、最高気温が10℃に届かない真冬のような寒さになるようです。暖かくして過ごしましょう。
さて、今回は平成29年度都立高校数学入試問題を取り上げます。
問題は、共通問題に出題された大問2の創作問題で、それは、
「ある中学校で、Sさんが作った問題をみんなで考えた。
次の各問に答えよ。
[Sさんが作った問題]
下の図1のように、上から順に、1段目に2個、2段目に3個、3段目に4個と、1段ごとに1個ずつマスを増やし、左端のマスが縦にそろうように10段目まで、並べたものを考える。
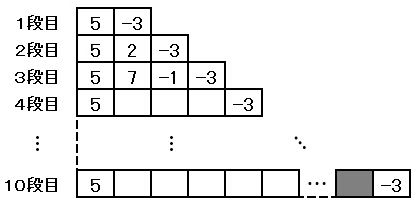
▲図1.問題図(1)
全ての段の左端のマスに5、右端のマスに-3を入れる。
2段目以降にある両端のマス以外のそれぞれのマスに、1つ上の段にある真上のマスと、その左隣のマスに入っている2つの数の和を入れる。例えば、2段目の中央のマスには、1段目の-3と1段目の5の和である2が入る。
このとき、10段目ある■で示したマスに入る数を考えてみよう。
なお、図1は、全て段の左端のマスに5、右端のマスに-3を入れ、両端のマス以外のそれぞれのマスについて、2段目、3段目の順に、3段目まで数を入れた場合を示している。
[問1] [Sさんが作った問題]で、10段目にある■で示したマスに入る数を、次のア~エのうちから選び、記号で答えよ。
ア -22 イ -19 ウ 37 エ 42
先生は、[Sさんが作った問題]をもとにして、次の問題を作った。
[先生が作った問題]
下の図2は、上から順に、1段目に2個、2段目に3個、3段目に4個と、1段ごとに1個ずつマスを増やし、左端のマスが縦にそろうように5段目まで並べたものである。

▲図2.問題図(2)
図3は、図2において、全ての段の左端マスに1、右端のマスに4を入れ、2段目以降にある両端のマス以外のそれぞれのマスに、1つ上の段にある真上のマスと、その左隣のマスに入っている2つの数の和を入れたものである。
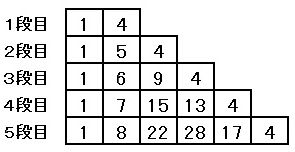
▲図3.問題図(3)
図3のそれぞれの段において、全てのマスに入っている数の和について考えると、
1段目は、1+4=5
2段目は、1+5+4=10=5×2
3段目は、1+6+9+4=20=5×4
4段目は、1+7+15+13+4=40=5×8
5段目は、1+8+22+28+17+4=80=5×16となり、
2段目以降のそれぞれの段において、全てのマスに入っている数の和は、1段目の2個のマスに入っている数の和である5の倍数となっている。
図2において、全ての段の左端のマスに入れる数をa、右端のマスに入れる数をbとし、2段目以降にある両端のマス以外のそれぞれのマスに、1つ上の段にある真上のマスと、その左隣のマスに入っている2つの数の和を入れるとき、5段目にある6個のマスに入っている数の和は、1段目の2個のマスに入っている数の和の16倍となることを確かめなさい。
ただし、a、bは自然数とする。
[問2] [先生が作った問題]で、5段目にある6個のマスに入ってい数をそれぞれa、bを用いた式で表し、5段目にある6個のマスに入っている数の和は、1段目の2個のマスに入っている数の和の16倍となることを証明せよ。」
です。
まず、[問1]です。
n段目の右端から1つ目のマスの数は、n-1段目の右端から1つ目のマスの数から3を引いたものです。
したがって、10段目にある■で示したマスに入る数は、5+(-3)×(10-1)=5-27=-22で、答えは ア になります。
続いて[問2]です。
全ての段の左端のマスに入れる数をa、右端に入れる数をbとすると、図4のようになります。

▲図4.全ての段の左端のマスにa、右端のマスにbを入れました
ここで、問題に与えられた方法で、図4の空いているマスに数を入れると、図5のようになります。
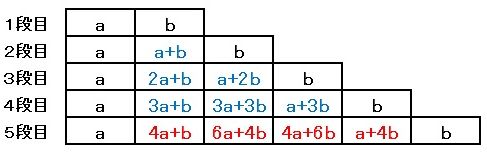
▲図5.空いているマスに数を入れました
5段目の6個のマスに入っている数は、左から、a、4a+b、6a+4b、4a+6b、a+4b、b で、これらの和は、
a+4a+b+6a+4b+4a+6b+a+4b+b=16a+16b=16(a+b)
です。
一方、1段目の2個のマスに入っている数の和はa+bです。
したがって、5段目の6個のマスに入っている数の和は、1段目の2個のマスに入っている数の和の16倍です。
例年より問題文が長く判り難かったかもしれません。
東西に長くのびた前線を伴う南岸低気圧の影響で、気温がぐっと下がりました。さらに明日も下がって、最高気温が10℃に届かない真冬のような寒さになるようです。暖かくして過ごしましょう。
さて、今回は平成29年度都立高校数学入試問題を取り上げます。
問題は、共通問題に出題された大問2の創作問題で、それは、
「ある中学校で、Sさんが作った問題をみんなで考えた。
次の各問に答えよ。
[Sさんが作った問題]
下の図1のように、上から順に、1段目に2個、2段目に3個、3段目に4個と、1段ごとに1個ずつマスを増やし、左端のマスが縦にそろうように10段目まで、並べたものを考える。

▲図1.問題図(1)
全ての段の左端のマスに5、右端のマスに-3を入れる。
2段目以降にある両端のマス以外のそれぞれのマスに、1つ上の段にある真上のマスと、その左隣のマスに入っている2つの数の和を入れる。例えば、2段目の中央のマスには、1段目の-3と1段目の5の和である2が入る。
このとき、10段目ある■で示したマスに入る数を考えてみよう。
なお、図1は、全て段の左端のマスに5、右端のマスに-3を入れ、両端のマス以外のそれぞれのマスについて、2段目、3段目の順に、3段目まで数を入れた場合を示している。
[問1] [Sさんが作った問題]で、10段目にある■で示したマスに入る数を、次のア~エのうちから選び、記号で答えよ。
ア -22 イ -19 ウ 37 エ 42
先生は、[Sさんが作った問題]をもとにして、次の問題を作った。
[先生が作った問題]
下の図2は、上から順に、1段目に2個、2段目に3個、3段目に4個と、1段ごとに1個ずつマスを増やし、左端のマスが縦にそろうように5段目まで並べたものである。

▲図2.問題図(2)
図3は、図2において、全ての段の左端マスに1、右端のマスに4を入れ、2段目以降にある両端のマス以外のそれぞれのマスに、1つ上の段にある真上のマスと、その左隣のマスに入っている2つの数の和を入れたものである。

▲図3.問題図(3)
図3のそれぞれの段において、全てのマスに入っている数の和について考えると、
1段目は、1+4=5
2段目は、1+5+4=10=5×2
3段目は、1+6+9+4=20=5×4
4段目は、1+7+15+13+4=40=5×8
5段目は、1+8+22+28+17+4=80=5×16となり、
2段目以降のそれぞれの段において、全てのマスに入っている数の和は、1段目の2個のマスに入っている数の和である5の倍数となっている。
図2において、全ての段の左端のマスに入れる数をa、右端のマスに入れる数をbとし、2段目以降にある両端のマス以外のそれぞれのマスに、1つ上の段にある真上のマスと、その左隣のマスに入っている2つの数の和を入れるとき、5段目にある6個のマスに入っている数の和は、1段目の2個のマスに入っている数の和の16倍となることを確かめなさい。
ただし、a、bは自然数とする。
[問2] [先生が作った問題]で、5段目にある6個のマスに入ってい数をそれぞれa、bを用いた式で表し、5段目にある6個のマスに入っている数の和は、1段目の2個のマスに入っている数の和の16倍となることを証明せよ。」
です。
まず、[問1]です。
n段目の右端から1つ目のマスの数は、n-1段目の右端から1つ目のマスの数から3を引いたものです。
したがって、10段目にある■で示したマスに入る数は、5+(-3)×(10-1)=5-27=-22で、答えは ア になります。
続いて[問2]です。
全ての段の左端のマスに入れる数をa、右端に入れる数をbとすると、図4のようになります。

▲図4.全ての段の左端のマスにa、右端のマスにbを入れました
ここで、問題に与えられた方法で、図4の空いているマスに数を入れると、図5のようになります。

▲図5.空いているマスに数を入れました
5段目の6個のマスに入っている数は、左から、a、4a+b、6a+4b、4a+6b、a+4b、b で、これらの和は、
a+4a+b+6a+4b+4a+6b+a+4b+b=16a+16b=16(a+b)
です。
一方、1段目の2個のマスに入っている数の和はa+bです。
したがって、5段目の6個のマスに入っている数の和は、1段目の2個のマスに入っている数の和の16倍です。
例年より問題文が長く判り難かったかもしれません。