こんにちは。東久留米市の学習塾塾長です。
今回は、2021年日本数学オリンピック予選の問題です。
問題は、
「正の整数nに対して、正の整数mであってmとnが互いに素であり、m+1とn+1も互いに素となるようなもののうち最小のものをf(n)で表す。このとき、

のうちに現れる正の整数は何種類あるか。」
です。
素数を小さい順に、
p1,p2,・・・,pk,・・・,pl
(k、lは正の整数、k≦l)
として、

とします。
このとき、αxは整数で、
α1,α2,・・・,αk-1≧1
αk=0
αk+1,・・・,αl≧0
です。(つまり、pkがn+1の約数ではない最小の素数になります)
初めに、
1≦m<pk-1
を満たすmを調べます。
上記の不等式の各辺に1を加えると、
2≦m+1<pk
になり、これからm+1はpkより小さい素数prを因数にもちます。
このとき、prはp1、p2、・・・、pk-1のいずれかで、するとprはn+1の約数になり、n+1とm+1は互いに素ではありません。
したがって、条件を満たすmは、
m≧pk-1
になり、
f(n)≧pk-1 (★)
です。
次に、
pk-1<pk
から、pk-1の約数は p1、p2、・・・pk-1 のいずれかなので、

と表すことができます。
このとき、βxは整数で、
β1,β2,・・・,βk-1≧0
です。
すると、
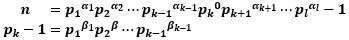
から、nとpk-1は互いに素で、さらに、

から、n+1とpkも互いに素になります。
これは、pk-1はmの条件を満たす整数であることを示していて、このとき(★)から、pk-1がmの最小値になるので、
f(n)=pk-1
であることが判りました。
続いて、
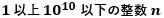
について、最大になるpkを求めます。
そこで、素数を小さい方から順に掛け合わせいくと、

から、pkの最大値は31です。
(2から31までの素数を1つずつ掛け合わせた積が

を超えるので、

以下の整数のなかに2から31までのすべての素数で割り切れるものはありません)
したがって、pkがとりうる値は、
2、3、5、7、11、13、17、19、23、29、31
の11種類で、これらのそれぞれについて、条件を満たす最小のm、つまり、f(n)が、
1、2、4、6、10、12、16、18、22、28、30
になるようなnが存在することを確かめればお仕舞です。

のとき、n+1と互いに素になる最小のm+1は31で、したがって、

です。
同様に、
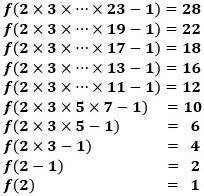
になり、11種類のf(n)に対して、
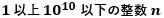
が存在します。
以上から、

に現れる正の整数は 11 種類 で、これが答えです。
簡単な問題です。
今回は、2021年日本数学オリンピック予選の問題です。
問題は、
「正の整数nに対して、正の整数mであってmとnが互いに素であり、m+1とn+1も互いに素となるようなもののうち最小のものをf(n)で表す。このとき、

のうちに現れる正の整数は何種類あるか。」
です。
素数を小さい順に、
p1,p2,・・・,pk,・・・,pl
(k、lは正の整数、k≦l)
として、

とします。
このとき、αxは整数で、
α1,α2,・・・,αk-1≧1
αk=0
αk+1,・・・,αl≧0
です。(つまり、pkがn+1の約数ではない最小の素数になります)
初めに、
1≦m<pk-1
を満たすmを調べます。
上記の不等式の各辺に1を加えると、
2≦m+1<pk
になり、これからm+1はpkより小さい素数prを因数にもちます。
このとき、prはp1、p2、・・・、pk-1のいずれかで、するとprはn+1の約数になり、n+1とm+1は互いに素ではありません。
したがって、条件を満たすmは、
m≧pk-1
になり、
f(n)≧pk-1 (★)
です。
次に、
pk-1<pk
から、pk-1の約数は p1、p2、・・・pk-1 のいずれかなので、

と表すことができます。
このとき、βxは整数で、
β1,β2,・・・,βk-1≧0
です。
すると、
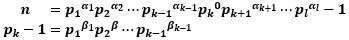
から、nとpk-1は互いに素で、さらに、

から、n+1とpkも互いに素になります。
これは、pk-1はmの条件を満たす整数であることを示していて、このとき(★)から、pk-1がmの最小値になるので、
f(n)=pk-1
であることが判りました。
続いて、
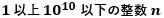
について、最大になるpkを求めます。
そこで、素数を小さい方から順に掛け合わせいくと、

から、pkの最大値は31です。
(2から31までの素数を1つずつ掛け合わせた積が

を超えるので、

以下の整数のなかに2から31までのすべての素数で割り切れるものはありません)
したがって、pkがとりうる値は、
2、3、5、7、11、13、17、19、23、29、31
の11種類で、これらのそれぞれについて、条件を満たす最小のm、つまり、f(n)が、
1、2、4、6、10、12、16、18、22、28、30
になるようなnが存在することを確かめればお仕舞です。

のとき、n+1と互いに素になる最小のm+1は31で、したがって、

です。
同様に、
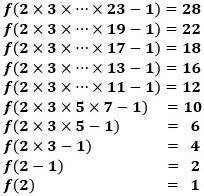
になり、11種類のf(n)に対して、
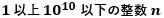
が存在します。
以上から、

に現れる正の整数は 11 種類 で、これが答えです。
簡単な問題です。




















