こんにちは。東久留米市の学習塾塾長です。
昨日と比べるとぐっと気温が下がりましたが、外出時に手袋が絶対必要というほどでもなく、なれなりの寒さになりました。これからしばらく冬日もなく、同じような天気が続くようです。
さて、今回は平成29年度灘中入試問題を取り上げます。
問題は、
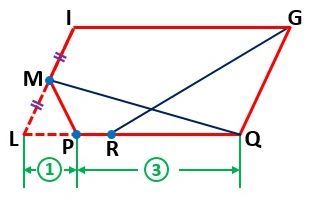
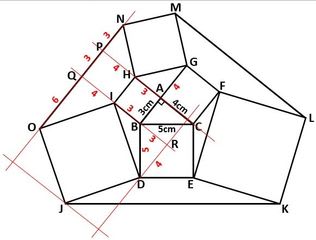
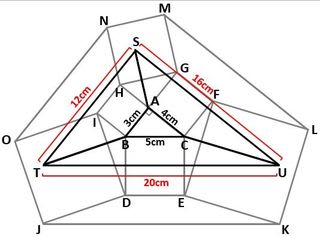
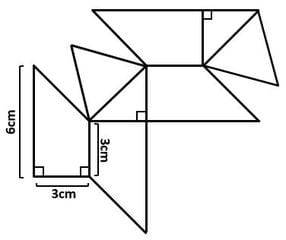
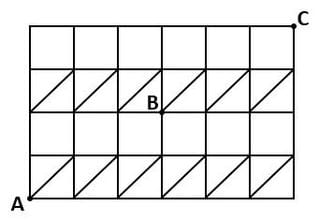
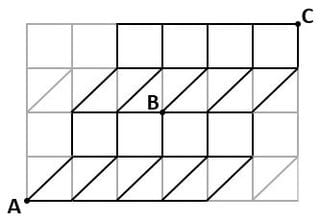
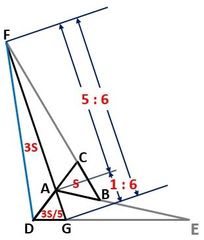
「図1のような長方形の細長い紙を3つの折り目で折り込み、図2のようにしました。5個の点A、B、C、D、Eを頂点とする五角形は正五角形です。また、点FはAEの真ん中の点です。

▲図1.問題図

▲図2.問題図
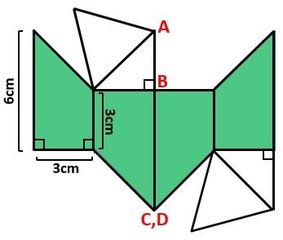
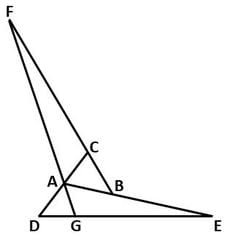
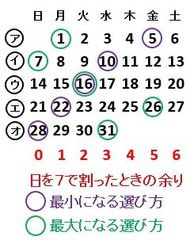
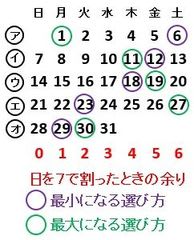
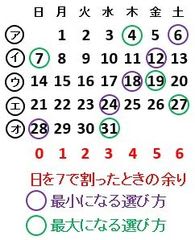
(1)紙を折り込むと、下の図すべての黒点は図2の点A、B、C、D、Eのどれかの位置に来ます。9か所の空欄にA、B、C、D、Eのうち当てはまるものをを記入しなさい。
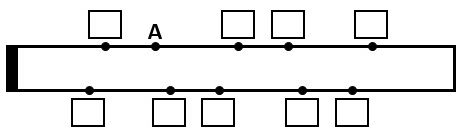
▲解答図(1)
(2)図2の紙を直線CFに沿ってはさみで切るとき、切り口を下の図に書き込みなさい。なお、下の図の黒点は(1)の図と同じ位置にあります。」
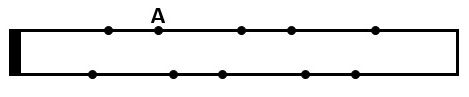
▲解答図(2)
です。
早速、取り掛かりましょう。
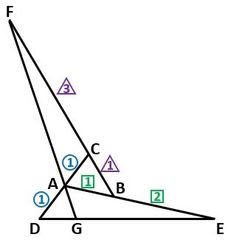
(1)は図3のように、図1の上と下の辺をなぞっていけばOKでしょう。
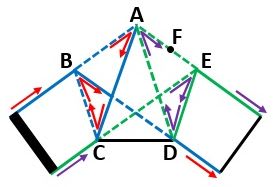
▲図3.上の辺(青色)と下の辺(緑色)をB、Cの左から出発してなぞりました
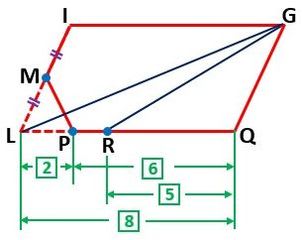
その結果、上の辺では、B→A→C→B→Dになり、下の辺では、C→E→D→A→Eになります。
したがって、答えは図4です。
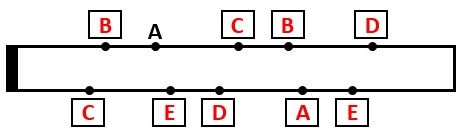
▲図4.(1)の答え
続いて(2)です。
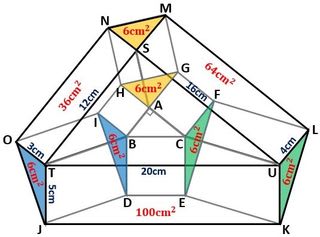
まず図5のように、正五角形に折り込んだものを手前から1枚ずつ切り取りましょう。
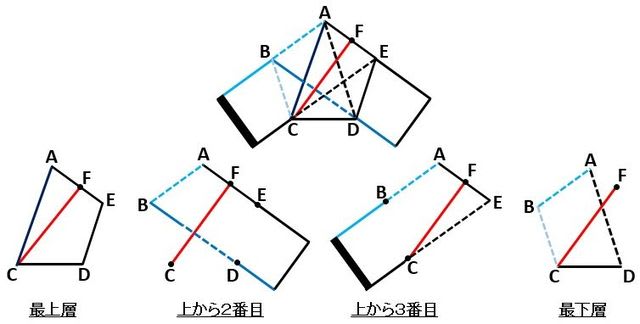
▲図5.正五角形に折り込んだものを手前から1枚ずつ切り取りました
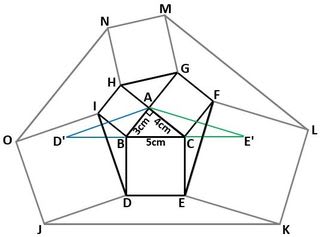
そして図6のように、これらの切り取った4つの部分を元の紙の状態に並べ替えます。
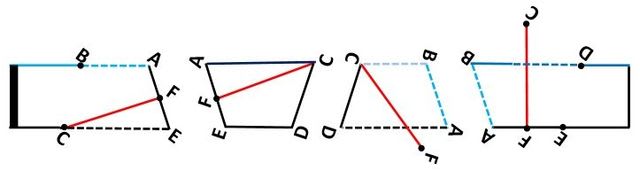
▲図6.切り取った4つの部分を元の紙の状態に並べ替えました
これらの4つの部分をくっつけると、図7のようになり、これが(2)の答えです。

▲図7.(2)の答え
面白い問題です。
昨日と比べるとぐっと気温が下がりましたが、外出時に手袋が絶対必要というほどでもなく、なれなりの寒さになりました。これからしばらく冬日もなく、同じような天気が続くようです。
さて、今回は平成29年度灘中入試問題を取り上げます。
問題は、
「図1のような長方形の細長い紙を3つの折り目で折り込み、図2のようにしました。5個の点A、B、C、D、Eを頂点とする五角形は正五角形です。また、点FはAEの真ん中の点です。

▲図1.問題図

▲図2.問題図
(1)紙を折り込むと、下の図すべての黒点は図2の点A、B、C、D、Eのどれかの位置に来ます。9か所の空欄にA、B、C、D、Eのうち当てはまるものをを記入しなさい。

▲解答図(1)
(2)図2の紙を直線CFに沿ってはさみで切るとき、切り口を下の図に書き込みなさい。なお、下の図の黒点は(1)の図と同じ位置にあります。」

▲解答図(2)
です。
早速、取り掛かりましょう。
(1)は図3のように、図1の上と下の辺をなぞっていけばOKでしょう。

▲図3.上の辺(青色)と下の辺(緑色)をB、Cの左から出発してなぞりました
その結果、上の辺では、B→A→C→B→Dになり、下の辺では、C→E→D→A→Eになります。
したがって、答えは図4です。

▲図4.(1)の答え
続いて(2)です。
まず図5のように、正五角形に折り込んだものを手前から1枚ずつ切り取りましょう。

▲図5.正五角形に折り込んだものを手前から1枚ずつ切り取りました
そして図6のように、これらの切り取った4つの部分を元の紙の状態に並べ替えます。

▲図6.切り取った4つの部分を元の紙の状態に並べ替えました
これらの4つの部分をくっつけると、図7のようになり、これが(2)の答えです。

▲図7.(2)の答え
面白い問題です。