※整数の余りと数列の漸化式。
実質的には高校1年生レベルで非常に良く出るテーマです。
東大数学は「見た目ほど難しくない」ことに気づくまでが勝負か？
（1）（2）は確実に得点したい。
桜で鍛えれば「偏差値40からの東大数学8割越え」も夢ではない。
東大数学の思考の流れを桜で体感しよう！
Do it now !
東大・京大・数学について（東大文系数学）
1の鋭角三角形はベクトル使って式だけ書いた
2の確率は図を書き間違えて爆死
3の微積はセンター試験レベルなのに完答できず（情けない）
4の整数は合同式使えず2項定理で大幅な時間ロス
家に帰って久しぶりに泣いた
東大・京大・数学について（京大理系数学）
1は途中の因数分解できずに放置
2の整数は合同式やってへんし苦手やからパス
3の四面体でベクトル使って撃沈（これが痛い）
4は平面ｙ＝ｚで放心状態になり図が書けへん
5は混乱して問題文読み間違えて上手く漸化式に表せない
6の係数が複素数みて窒息死した
試験後しばらく身動きできんかった
東大・京大・数学について（東大理系数学）
1の証明は難しく考えすぎて途中まで
2は漸化式なんかいらんのに勝手に自爆して
簡単な3をパスして（最大の失敗）
4の複素数平面はx+yiを代入して計算地獄
5は問題意味不明で大幅な時間ロス
6の体積は図書いただけで終わった
あっと言う間の出来事だった
1000以下の素数は250個以下であることを示せ。
ＨＩＮＴ。
1050に注目するのがポイント！
数学力で計算量を減らすべし。
普通の解法1
普通の解法2
普通の解法3
普通の解法4
＜京都大学・文系・数学・第3問＞
＜コメント＞
2^12＝1331（n進法）のとき、n はいくつか。10進法で答えよ。
まず、与式を10進法で表す。（できるかな？）
n=4,5,6,7,8,・・・と様子を見ていけば見えてくる。（実験：試し打ち）
2^(n＋2)＝n^3＋3n^2＋3n＋1（10進法）
＜ヒント：戦略で学ぶ数学＞
さくらの個別指導で使用するプリント
※4次方程式、ｔａｎ、虚数解、少なくとも一つ･･･これらの言葉に惑わされているようではまだまだ勉強不足。
典型問題をひと通りマスターしてから京大数学が始まります。
東大数学に比べて計算量は少なくてすむし色々と工夫されているので面白い。
桜で鍛えれば「偏差値40からの京大数学8割越え」も夢ではない。
※座標空間、3点を通る平面、対称な点Ｅ･･･これらの言葉に惑わされているようではまだまだ勉強不足。（普通の先生は「平面の方程式」について知らないが）
典型問題をひと通りマスターしてから京大数学が始まります。
本問は「意欲的に発展事項まで勉強していた受験生」にご褒美を与えよう！という東大京大数学らしい問題です。
少し説明すると、
ax+by+c=0・・・・・直線の方程式（中学で学習）
ax+by+cz+d=0・・・平面の方程式（大学で学習）
上の2つの式はどこか似てるよね。
直線の方程式にある（a,b）は何を表しているのか？が分かれば（a,b,c）の意味も分かるはず。
桜で鍛えれば「偏差値40からの京大数学8割越え」も夢ではない。
数学で遊ぼう！
※実数、複素数平面、三角形の3頂点、重心･･･これらの言葉に惑わされているようではまだまだ勉強不足。
教科書をひと通りマスターしてから東大数学が始まります。
1つの問題の中に各分野の色々な要素が含まれている東大京大数学らしい総合問題。
まずは問題文の数学用語、意味を正確に把握するところから始まります。
1つ1つは教科書レベルなのに解けない。
そんな問題が多い。
桜で鍛えれば「偏差値40からの東大数学8割越え」も夢ではない。
数学を楽しもう！
東大・京大・数学について（京大文系数学）
1は領域の計算で手間取り大幅な時間ロス
2の確率は最低ｘ回として式が作れない
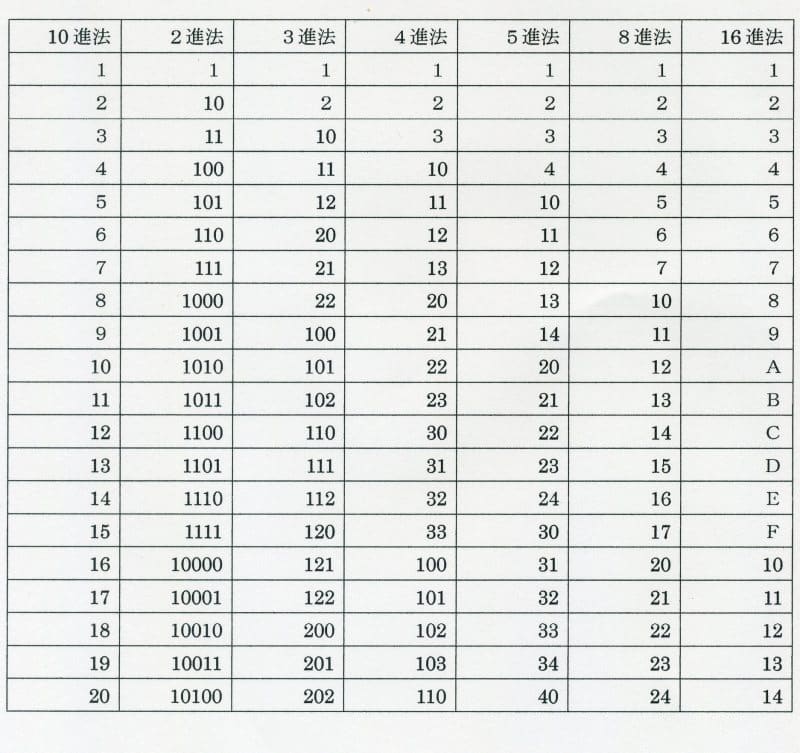
3のｎ進法は最初の方程式を10進法に直せなかった
4の四面体は適当に作文してチョロまかし
5の３次式は解と係数の関係だけ書いて部分点狙い
全問手を付け知ってる知識を書きまくった
採点は厳しいらしいがその通りみたいな結果だった
ＨＩＮＴ。
4.空間ベクトル、5.3で割った時の余りで分類（合同式≡ｍｏｄ）
三角形の面積を求めるベクトル公式、ｍｏｄなどを駆使し
数学力で計算量を減らすべし。
※ある区間で定義された関数、～を示せ･･･これらの言葉に惑わされているようではまだまだ勉強不足。
典型問題をひと通りマスターしてから京大数学が始まります。
本問は珍しく初めからグラフが与えられているが「最初の１手をどうしよう？」という東大京大数学らしい問題です。
理科なんかだと問題を見た瞬間「やるべき事」が浮かんでくるのだが。
この辺が数学の難しいところです。
きほん全く同じ問題は出ませんから。
積分の値がマイナス？
積分で面積を求めるとき、グラフは書かないと駄目？というのはよく狙われます。
また、自分で演習するとき答えばかりに目が行くがそれよりも
１問１問味わって演習するのが大切です。
桜で鍛えれば「偏差値40からの京大数学8割越え」も夢ではない。
数学で遊ぼう！
