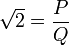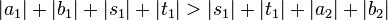「中学生のころ、数学者である叔父に「数論の3つの真珠」(日本評論社)という本をもらいました。
ロシア人数学者の著者が、長年数学者たちを悩ませてきた難問を解説しています。
180ページほどの本ですが、載っている問題は3問だけ。
数十ページを割いて1問を読み解いているのです。
難問とはいえ、基礎としている知識はすべて、小学生でもわかる非常にシンプルなものです。
「魔法みたい」と感じ、数学の魅力に取りつかれました。
大学受験のころを振り返ると、苦手としていた科目はとくにありませんでした。
それだけを聞くとまるですごそうに聞こえるのですが、私は他の方に比べ、学んだ時間がきっと長いのです。
寝食を忘れのめりこんだ時期が、どの教科にもありました。数学でいうと、食事をしているときも授業中もずっと問題を考えていて、1、2カ月後に「解けた!」などということもありました。
そういうときは「あれも違う」「これも違う」と頭の中で山ほど失敗して挫折して悪戦苦闘して、だんだん考えが研ぎ澄まされていきます。
徐々にその問の本質のようなものが見えてきて、少し気が抜けたときにふっともう一回考える…そんなときに急に問題が解けることもあります。
数学の問題を解くことは、山登りに似ていると感じています。」













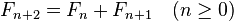

 は
は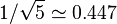 が最大で、それを超えることはない。従って、第2項を略した次の式は Fn の値を 0.447 以下(n > 4 のとき1%以下)の誤差で与える
が最大で、それを超えることはない。従って、第2項を略した次の式は Fn の値を 0.447 以下(n > 4 のとき1%以下)の誤差で与える
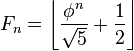
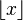 は
は