<問題>
<解答>
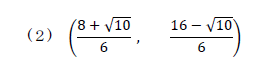
<コメント>
三角形の内心点を求める問題。
角の2等分線に注目する。
やや易。
黄金比(おうごんひ、英語: golden ratio)は、

の比である。近似値は1:1.618、約5:8。
線分を a, b の長さで 2 つに分割するときに、a : b = b : (a + b) が成り立つように分割したときの比 a : b のことであり、最も美しい比とされる。貴金属比の1つ(第1貴金属比)。
黄金比において
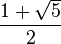
は、二次方程式 x2 - x - 1 = 0 の正の解であり、これを黄金数(おうごんすう、英語: golden number)という。しばしばギリシア文字のφ(ファイ)で表されるが、τ(タウ)を用いる場合もある。
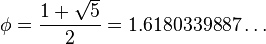
黄金数には,次のような性質がある。
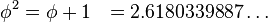
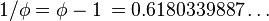
黄金比は中末比(ちゅうまつひ)や外中比(がいちゅうひ)とも呼ばれる。a : b = b : (a + b) が成り立つとき、a を末項(まっこう)、b を中項(ちゅうこう)という。
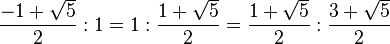
上式を小数の近似値で表示すると、0.618 : 1 ≒ 1 : 1.618 ≒ 1.618 : 2.618 となる。
黄金数は次のような美しい連分数表示をもつ。
![phi = 1 + cfrac{1}{1 + cfrac{1}{1 + cfrac{1}{1 + cfrac{1}{ddots}}}} = [1;1,1,1,1,ldots]](http://upload.wikimedia.org/math/5/e/9/5e9055644970505264ff342b83fd97f2.png)
次のような表示ももつ。
![phi^{-1} = [0; 1, 1, 1, ldots] = 0 + cfrac{1}{1 + cfrac{1}{1 + cfrac{1}{1 + ddots}}}](http://upload.wikimedia.org/math/a/1/c/a1c41263f154a50ca3718ba9ea301221.png)



三角関数を使うと次のように表すことができる。

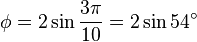

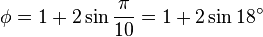
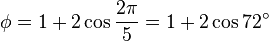



フィボナッチ数列の隣り合う 2 項の比は黄金比に収束する。また、 1, φ, φ2, φ3, φ4, ... という等比数列を考えたとき、1 + φ = φ2 を利用すると
となり、係数にフィボナッチ数列が出現する。フィボナッチ数列の第 n 項を Fn とすると、φn は次のようになる。
黄金比で長さを分けることを黄金比分割または黄金分割という。
幾何学的には正五角形や五芒星(星形:☆)から容易に得ることができる。正五角形の一辺と対角線の比、五芒星を構成する線分と頂点を結ぶ線分の比は、黄金比となる。
京都大は13日、一般入試に先駆け、今年度から実施している「特色入試」で初めての合格発表を行った。
発表が行われたのは全10学部で唯一、大学センター試験を受験する必要がない医学部医学科(定員5人)で、受験生5人に対し、合格者はわずか1人だった。
医学部医学科の合格者について、京大は「(高校2年生の)飛び級の合格者ではない」(広報課)と説明。合格者が1人にとどまった理由は「答えられない」(医学部)とした。
整数論の華である類体論は、高木貞治が発表し、アルティンによって完成した理論です。 数学は自然科学の王であり、整数論は数学の女王であるといわれていますが、整数論の中でもとりわけ類体論は極めて美しい理論です。 しかしながら、類体論を理解するには、最低限、郡論/体論/ガロア理論が前提となります。
そもそも、整数論は、方程式の整数解を求めるところから始まりました。古代ギリシャ時代より直角三角形がピタゴラスの定理( ![]() )を満たすことは知られていましたが、このピタゴラスの定理を満たす整数解が無限にあることも知られていました。
)を満たすことは知られていましたが、このピタゴラスの定理を満たす整数解が無限にあることも知られていました。
方程式の整数解を求める場合に、有効な方法の1つとして、方程式の![]() をとる方法があります。
をとる方法があります。![]() とは、
とは、![]() (素数)で割った余りを考えるということです。フェルマーは
(素数)で割った余りを考えるということです。フェルマーは![]() の世界において、多数の法則を発見しましたが、オイラーは更にそれを一般化して平方剰余の相互法則を発見し、ガウスが証明しました。 平方剰余の相互法則とは、2次方程式を
の世界において、多数の法則を発見しましたが、オイラーは更にそれを一般化して平方剰余の相互法則を発見し、ガウスが証明しました。 平方剰余の相互法則とは、2次方程式を![]() した場合の解の有無を記述する美しい法則です。
した場合の解の有無を記述する美しい法則です。 ![]() の間に美しい調和があることが分かります。更に、それを一般化したものが、高木貞治に端を発する類体論です。
の間に美しい調和があることが分かります。更に、それを一般化したものが、高木貞治に端を発する類体論です。
類体論の入門書については、既に、多数の良書があります。にもかかわらず、なぜ、類体論の入門を記載する気になったのか、1つには郡論/体論/ガロア理論を知らない高校生/社会人に少しでもこの美しい理論を知ってもらいたかったからです。もう1つは、方程式の解の有無という整数論の原点に立ち返って類体論を記述したかったからです。
方程式が![]() で解けるか否かは、クンマーらの努力により、素イデアルの分解と同値であることが示されました。そこで、古典的類体論は、アーベル拡大における素イデアルの分解の法則を示す理論になります。しかし、素イデアルの分解は本来方程式の分解に対応するものです。方程式の分解を通じて類体論を記述したい、そんな素朴な想いにより書き始めました。
で解けるか否かは、クンマーらの努力により、素イデアルの分解と同値であることが示されました。そこで、古典的類体論は、アーベル拡大における素イデアルの分解の法則を示す理論になります。しかし、素イデアルの分解は本来方程式の分解に対応するものです。方程式の分解を通じて類体論を記述したい、そんな素朴な想いにより書き始めました。
できるだけ高校生に理解できるよう、群論やガロア理論を知らない人にも読めるように記載していくよていです。といっても、これらを丁寧に解説しようとすると1つ1つで本ができてしまいます。群論やガロア理論は基本書が多数出ていますので、できるだけ簡単な基本書を1冊読まれることをお勧めします。
難しい数学の知識が、日常生活で直接的に役に立つことは少ないかもしれませんが、論理的な思考力を養うことができます。
海外掲示板に、
「あなたの知ってるクールな数学の事実を教えてください」と質問の投稿がありました。
興味深い回答をご紹介します。
●y のx% = x のy%
y(x/100) = x(y/100)
yx/100 = xy/100
これは何の式かというと、「頭の中でパーセントの答えを計算したいときに、ひっくり返すだけでいい」ってことなんだ。
例1)50の2%はいくつ? これは2の50%と同じ。答えは1。
例2)75の4%はいくつ? これは4の75%と同じ。答えは3。
↑何てクールなんだ。よーし、消費税をそれで計算してみるよ。
「13ドルの13%は?」
くそっ。
●無理数を発見した人はそのことが理由で殺された。
(ピタゴラスの弟子ヒッパソスの無理数発見は妥当であったが、ピタゴラスは初め異端宗教のように取り扱い、彼らはヒッパソスを追放、もしくは殺害した。伝説によると、ヒッパソスは船上で無理数を発見し、ピタゴラスの弟子たちは彼をそのまま船外に投げ出したと伝えられている:Wikipedia)
●二次方程式には公式があり、三次や四次までは公式がある。しかし5次方程式以上に公式はない。
●「1」のほかには唯一「3435」だけが、各桁ごとに累乗した数字を足した合計と=になる。
33+ 44+ 33+ 55= 3435
●分母が7の分数を小数にすると、すべて同じ6つの数字の同じ順番の繰り返しになる。ただ始まる数字が異なるだけ。
1/7 = 0.142857142857...
2/7 = 0.285714285714...
3/7 = 0.428571428571...
4/7 = 0.571428571428...
5/7 = 0.714285714285...
6/7 = 0.857142857142...
↑こういうのを見ると、数学のいくつかは黒魔術だとか思ってしまう。
↑単に宇宙には順番があるだけなんだよ。
●6週間はきっちり10!(10の階乗)である。
(階乗:4×3×2×1のように整数を階段状に掛ける計算)
●1+1=2 を1冊使って説明している本がある。
●同じ部屋に23人いるとき、同じ誕生日がいる確率は50%。
●赤道をちょうど一周巻ける長さのロープがあるとしたら、それをさらに6.3m長くするだけで、地上から1m上空を巻ける。(半径が1m大きくなっても6.3m延長するだけで済む)
↑ついでにそれは水星、火星、木星、太陽についても同様である。
↑説明すると
地球の半径 = 6.3674447×106
地球の半径+1m =6.3674447×106+1m
円周 = 2πr
地球の円周 = 4.0007835×107
地球の円周+1m =4.0007841×107
上の2つの差:6m
●フィボナッチ数列(0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …)
は、1/89に含まれている。
1/89 = 0.01 + 0.001 + 0.0002 + 0.00003 + 0.000005 + 0.0000008 + 0.00000013 + 0.000000021 + 0.0000000034...
(フィボナッチ数 - Wikipedia)
●22/7は3.14よりも円周率に近い。
↑355/113はもっと近いぞ。
↑31415926535/10000000000はもっと近いぞ。
数字と向き合っているだけなのに、宇宙の真理に近づいている気持ちになるのが、数学の魅力かもしれませんね。
What's the coolest mathematical fact you know of?