『原論』第9巻命題20で、素数が無数に存在することが示されている。その証明は、次の通りである
- a, b, …, k を任意に与えられた素数のリストとする。その積 P := a × b × … × k に 1 を加えた数 P + 1 は、素数であるか、素数でないかのいずれかである。素数であれば、最初のリストに含まれない素数が得られたことになる。素数でなければ、何らかの素数 p で割り切れるが、p はやはり最初のリストに含まれない。なぜならば、リスト中の素数は P を割り切るので、P + 1 を割り切ることは不可能だからである。任意の素数のリストから、リストに含まれない新たな素数が得られるので、素数は無数に存在する。
この証明は、しばしば次のような形で表現される。
- 素数の個数が有限と仮定し、p1, … pn が素数の全てとする。その積 P = p1 × … × pn に 1 を加えた数 P + 1 は、p1, …, pn のいずれでも割り切れないので、素数でなければならない。しかし、これは p1, …, pn が素数の全てであるという仮定に反する。よって、仮定が誤りであり、素数は無数に存在する。
この形の証明のために、「ユークリッドは、背理法で素数が無数にあることを証明した」「ユークリッドの証明は、存在のみを示しており、具体的な構成の手続きを示していない」「ユークリッドは、最初のいくつかの素数の積に1を加えた数が素数であることを証明した」などの誤解をする者がいるが、いずれも正しくない。特に、最後の主張は 2 × 3 × 5 × 7 × 11 × 13 + 1 = 59 × 509 という反例により、歴史的にのみならず数学的に誤りである。
ドイツの有名な数学者ガウスは「整数は数学の女王である」と言ったそうです。数学の好きな人は少ないと思いますが、「数学者は特別な人」という様な憧れに近い感覚があるのではないかと思います。
私も「ガロアの生涯」や「フェルマーの最終定理」などの話を本を読んで、次は数学者の頭を持って生まれたいと思っております。そんなですからガウスさんの言葉の意味は残念ながら分かりません。
しかし、以下の式を見て整数の美しさ、むしろ神秘さを感じます。
1 × 1 = 1
11 × 11 = 121
111 × 111 = 12321
1111 × 1111 = 1234321
11111 × 11111 = 123454321
111111 × 111111 = 12345654321
1111111 × 1111111 = 1234567654321
11111111 × 11111111 = 123456787654321
111111111 × 111111111 = 12345678987654321
ある人たちは、ガウスの言葉について「女王は美しいが使われることはない」という意味であると申しております。確かに幾何学、解析学などが科学の進歩に結びついているのに対し、代数学に属する整数論は実用性とはやや離れている学問のような気がします。
上記の式は日常的な何かに直接役立ちそうな気はしませんが、整数の不思議な美しさを感じます。
東大を目指す生徒にとっては、センター試験はあくまでも2段階選抜の1つの手段でしかない。東大の場合はセンター試験の得点が900点満点から110点満点に圧縮される。2次試験が440点満点で、合計550点満点。「350点」取れば、最難関の理Ⅲ（医学部）を除き、東大には合格するといわれている。
2次試験は、文系の場合、英語120点、国語120点、数学80点、地理・歴史（2科目）120点。理系の場合、英語120点、国語80点、数学120点、理科（2科目）120点。
「350点」が合格点だとすれば、センター試験で9割取ったとして、圧縮して110点中の100点。合格点の350点から引くと、2次試験で250点を取らなければならない。それをどの科目で何点取っていくかという戦略になる。
たとえば、文系で、数学が苦手だから35点、英語は得意だから85点取ると想定すると、あと130点を国語と地理・歴史でどう稼ぐかになる。
英語はリーディングの後にリスニングがある。リスニングの時間を軸にして、その前後でどの問題からどう解いていくかまで緻密にシミュレーションする。
東大の求める人材像
こうした2次試験で東大はどのような生徒を求めているのだろうか？ 生徒のどういう能力を問い、どういう生徒を求めているのか、東大は公表しているので紹介する
（以下、引用・抜粋）
・国語…文章を筋道立てて読み取る読解力と、それを正しく明確な日本語によって表す表現力。
・地理歴史…総合的な知識、知識を関連づける分析的思考力、論理的表現力。
・数学…数学的に思考する力、数学的に表現する力、総合的な数学力。
・理科…自然現象の本質を見抜く能力、原理に基づいて論理的かつ柔軟に思考する能力、自然現象の総合的理解力と表現力。
・英語…英語による受信力、英語による発信力、批判的な思考力。
以前、ハーバード大学の学生に、東大の数学と理科の入試問題を見てもらったことがある。その学生は「全米の学力テストのSATは、難易度も低く、マークシートなので満点が取れる。しかしながら東大の入試問題は、難易度も非常に高く、答案に記述していかないといけないので満点は取りにくい。もしかすると世界で最も難しい大学入試の問題かもしれない」と言っていたのが印象的だった。
また入試問題だけでなく、毎年約9000人もの受験生が書き上げた4教科の答案を限られた期間の中で採点し、その答案のみで、大学が求める人材を見抜くという「東大の選抜する技術」は、ある意味、世界でトップかもしれない。
今回は逆手流という活用範囲が広い手法について解説します。
とくに、関数の値域を求める問題や軌跡・領域の問題などで効果があり、解法の方針が立てやすくなるというのが最大のメリットです。
ということで、「逆手流とはいったいどのような考え方なのか」から説明していきたいと思います。
まずは言葉の説明から。
関数 y = f(x) において、xを独立変数(インプット)、yを従属変数(アウトプット)といいます。このとき、yのとり得る値を求めたいとしましょう。
ふつうは独立変数のもとで従属変数のとり得る値を考えます(これを自然流もしくは順像法といいます)が、
逆手流では独立変数と従属変数を逆に捉えようという考え方をします。
わかりやすく言えば、xを動かすのではなく、yを動かすということです。
では、簡単な例題で逆手流の使い方を具体的に解説していきます。
【例題1】 -1 ≦ x ≦ 2 のとき, y = x - 2 の値域を求めよ.
例えば、
y = 1 となり得るでしょうか？ このとき、x = 3 であり -1 ≦ x ≦ 2 を満たさないので、y = 1 とはなり得ないことがわかります。
y = 0 となり得るでしょうか？ このとき、x = 2 であり -1 ≦ x ≦ 2 を満たすので、y = 0 となり得ることがわかります。
y = -5 となり得るでしょうか？ このとき、x = -3 であり -1 ≦ x ≦ 2 を満たさないので、y = -5 とはなり得ないことがわかります。
このように、y = k となり得るかと従属変数yを独立変数として捉えます。
つまり、y = k となり得るとはどういうときかと考えて同値変形を施します。
y = k となり得るとする → x = k + 2 → -1 ≦ k + 2 ≦ 2 を満たせばよい と考えて
-3 ≦ k ≦ 0
∴-3 ≦ y ≦ 0
【例題2】 xがすべての実数値をとって変化するとき, y = x2 + 2x - 3 の値域を求めよ.
y = k となり得るとする → x2 + 2x - (3 + k) = 0 が実数解を持てばよい と考えて
判別式 D/4 = 1 + (3 + k) = 4 + k ≧ 0 ⇔ k ≧ -4
∴y ≧ -4
※xに範囲が付いている場合でも同様に考えて、2次方程式の解の配置の問題として捉えればＯＫですね。
【例題3】 xがすべての実数値をとって変化するとき, y = (x2 - 3x + 4)/(x2 + 3x + 4) の値域を求めよ.
y = k となり得るとする → (k-1)x2 + 3(k + 1)x + 4(k - 1) = 0 が実数解を持てばよい と考えて
k = 1 と k ≠ 1 で場合分けします。
() k = 1 のとき 6x = 0 より x = 0(実数) ∴y = 1 となり得る。
() k ≠ 1 のとき 判別式 D = 9(k + 1)2 - 16(k - 1)2 ≧ 0 ∴1/7 ≦ k ≦ 7
()()より 1/7 ≦ k ≦ 7
∴1/7 ≦ y ≦ 7
※微分(数Ⅲ)を用いて分数関数のグラフは描けますが、逆手流だとグラフを描かずとも求めることができます。
【例題4】 実数x, yが x2 + y2 = 1 を満たすとき, x + y の取り得る値の範囲を求めよ.
x + y = k となり得るとする → y = k - x → x2 + (k - x)2 = 1 → 2x2 - 2kx + (k2 - 1) = 0 が実数解を持てばよい と考えて
判別式 D/4 = k2 - 2(k2 - 1) ≧ 0 ⇔ -√2 ≦ k ≦ √2
∴-√2 ≦ x + y ≦ √2
【例題5】 0 ≦ x ≦ 1, 0 ≦ y ≦ 1 のとき, 点P(x + y, x - y)の動く領域を図示せよ.
点P(X, Y)が領域内の点とする → X = x + y, Y = x - y → x = (X + Y)/2, y = (X - Y)/2 → 0 ≦ (X + Y)/2 ≦ 1, 0 ≦ (X - Y)/2 ≦ 1 を満たせばよい と考えて
0 ≦ (X + Y)/2 ≦ 1 ⇔ 0 ≦ X + Y ≦ 2 ⇔ Y ≧ -X …①, Y ≦ -X + 2 …②
0 ≦ (X - Y)/2 ≦ 1 ⇔ 0 ≦ X - Y ≦ 2 ⇔ Y ≦ X …③, Y ≧ X - 2 …④
点P(X, Y)は①～④を同時に満たせばよい。
岡田康志（おかだ・やすし）1968年大阪府生まれ。93年東京大学医学部卒業。97年同大学院医学系研究科博士課程修了。医学博士。同年同大学医学部解剖学・細胞生物学教室助手。学部学生時代を含め20年余り同大学院医学系研究科の廣川信隆教授のもとでモーター分子キネシンの研究に取り組む。2011年理化学研究所生命システム研究センター（QBiC）細胞極性統御研究チーム・チームリーダー。大阪大学大学院生命機能研究科招聘教授を兼務。16年東京大学大学院理学系研究科理学部教授（物理学専攻）。
───小さいころはどんな子どもでしたか？
幼稚園のころから毎月発売される学研の図鑑を隅から隅まで読んでいるような子で、小学3、4年のころに抱いた将来の夢は、NASAに行って宇宙飛行士になって宇宙の研究をすることでした。
実験遊びみたいなことも好きで、アサガオなどを使った色水遊びをするんですが、酢を入れたら色が変わって、重曹を入れたらまた色が変わったと喜んでいたら、製薬会社に勤めていた父親からpH試験紙を渡されたので、それで家のまわりのものを次々と試してみた。おかげで幼稚園のころからpH7が中性で、それより小さい数値だと酸性、大きいとアルカリ性だというのを知っていました。ツバをペッとかけると弱アルカリだとか、漆喰や壁はアルカリが強いとか。
そうそう、あるときカマキリを捕まえてきて、カマキリは生きた餌しか食べないので毎日チョウやバッタを捕まえてきて餌をやっていたら、オスとメスだったので交尾をはじめた。交尾が終わるとメスがオスをバリバリと食べて、やがて卵からかえった赤ちゃんカマキリが部屋中にあふれ返ったのを覚えています。それが小学校の2、3年のころでしたね。
作ったり壊したりするのも好きで、時計ももちろん壊しているし、押し入れから真空管ラジオが出てきたのでそれを感電しながら壊して、また組み立てたり・・・。
───中学・高校と灘に進学して、灘高開校以来の天才とか、中・高校時代に30万ページの読書量を誇ったなどの「伝説」が残っていますが･･･。
30万ページというのは「伝説」というほど大変な話ではないし、とんでもない数字でもないですよ。毎日200ページ読めば300日で6万ページ、それを6年間続ければ36万ページですから、ごくふつうの数字はないですか？
たしかに本は片っ端から読みましたね。大阪の自宅から灘まで電車通学していましたので、片道１時間以上かかります。だから毎日往復で2時間以上。今だとスマホがありますが、当時は電車に乗っている間は本を読むぐらいしかすることがないんですよ。ですから、学校の図書館の本はすぐに大半を読んでしまって、灘高校の最寄り駅近くにある神戸市の図書館から借りて読んでいました。
───数多く読んだ本の中で、強い影響を受けた本などはありますか？
ファインマンとかランダウなどの物理の教科書ですね。ランダウは1962年にノーベル物理学賞を受賞した理論物理学者で、高校1年のときにクラスに来た教育実習生にいい本はないか聞いたら、彼とリフシッツの共著の教科書を教えてくれました。その中の『力学』を読んでみたのですが、とにかくブッ飛んだ本で、強烈でした。その解説をすると、どれだけ時間があっても足りない（笑）
───大阪ご出身で、高校時代に理論物理の本を読みふけっていながら、東大の理科III類を選んだのはなぜですか。
当時、物理学は超ひも理論や超伝導や今の観測的宇宙論などが続々と登場する前の谷間の時代でした。それならば、まだまだわからないことがたくさんある生物物理の分野もおもしろそうだなどと考えていたのです。
その点で東京大学は、入学時に学部を決める必要がなく、1－2年生の前期課程は駒場の教養学部に属して、2年の後期にそれまでの成績で学部・学科を決める「進学振り分け（進振り）」という制度があり、理科III類であれば、成績に関係なくどの学部にも行くことができるんです。選択肢の広さも魅力でした。
───駒場時代は、どんなふうに過ごしたのですか。
実はこの話をすると皆から呆れられるんですが、月曜から土曜日まで、全コマを埋めました。いくら単位を取っても学費はかわりませんから、トクじゃないですか。1年に100単位以上取ったんじゃないかなぁ。外国語も必修は第2外国語までですが、第2外国語でドイツ語を取って、そのほかにフランス語、ラテン語、ギリシャ語を取って、政治学も哲学も、とにかくおもしろそうな授業は全部受講しましたね。
───それで成績はいかがでしたか？
たしか平均が90数点じゃなかったかな。
(1)～(3)はパターン問題といってよいだろう。その後は中々大変である。解答が気になる人は、2003年入試問題研究：日本女大理＠青空学園数学科 へどうぞ。さて、全体としてみるとかなり重厚な問題だが、その結果として得られる(7)の最終的な結論は数学上計り知れない価値があるものである。(7)の極限を不等式で評価する問題は割とよく出題されるが、極限値そのものを明確に求める問題は難しく、一般入試では出題できないだろう。
以下で、素数に魅せられた数学者達の足跡を辿りながら式の背景に広がる数学の世界を堪能してもらいたい。
はじめに伝説となっている2人の数学界の巨人を紹介する。
18世紀最大の盲目の数学者レオンハルト・オイラー（スイス ; 1707～1783）
ニュートンが数学を自然界に応用し多くの科学的な実績を残していた18世紀初頭、オイラーはスイスで誕生した。人間離れした計算力と記憶力で膨大な計算を暗算で行うことができたオイラーは、数学のあらゆる分野、さらには物理学にも膨大な業績を残した。オイラーの公式、オイラー定数、オイラー方程式、オイラー関数、オイラー予想、一筆書きができる必要十分条件(オイラーグラフ)、オイラー線、オイラーの多面体定理など、様々な分野で頻繁にオイラーの名が登場する。π、sin、cos、e、i、y=f(x)など現在世界中で使用されている記号もオイラーが発明したものである。さらには、幾何学で表現されていたニュートン力学を「ma=F」という現在の解析的表現に変更したのもオイラーである。当時まだ市民権を得られていなかった虚数iを積極的に活用してその有用性を広めた功績も大きい。
オイラーは1年間に普通の数学者の一生分に相当する平均800ページもの論文を書いたため、人類史上最も多くの論文を書いた数学者であったと言われる。悪環境やストレスから、30歳になる頃には片目を、60歳になる頃には両目を失明してしまうが、論文を書くペースは全盲になっても全く変わることはなく76歳で亡くなるその日まで数学に没頭していたという。オイラーの論文は5万ページを超える全集にまとめられて1911年から刊行され続けているが、その全集は100年以上たった今日でも完結していない。
19世紀最大の数学者カール・フリードリヒ・ガウス（ドイツ ; 1777～1855）
オイラーと並び称され「数学王」との異名を取る人類最高の数学者の一人であり、近代数学のあらゆる分野で先駆的な役割を果たした。言葉を話せるようになる前から計算ができ、3歳のときに父親がしていた職人達に支払う給料の計算の誤りを指摘したという。また、小学生のときには1から100までの和を現在でいう等差数列の和の公式を用いて瞬時に求め、教師を驚かせた。18歳のときには最小2乗法の発見、19歳のときには合同式を用いた合同算術を発明し、平方剰余の相互法則を証明した。また、同時期に正17角形が定規とコンパスだけで作図可能なことも証明した。作図可能な正素数角形の発見は約二千年ぶりのことであった。学位論文では、代数学の基本定理「n次方程式は複素数の範囲でn個の解をもつ」に完全な証明を与えた。
正17角形が作図可能であることに興奮したガウスは、数学者になることを決意し、そのときから数学日誌をつけ始めたという。ガウスは性格上多くの結果を得ながらも公表しなかったが、この日誌のおかげでガウスの業績を確認できる。ガウスの業績は、代数学、数論、複素平面、関数論、非ユークリッド幾何学など広範囲に及び、電磁気学、天文学など物理学の発展にも大きく貢献した。そのことは、ガウス記号、ガウス曲率、ガウス関数、ガウス整数、ガウスの法則、ガウス平面、ガウス積分など、ガウスの名にちなんだものが多岐にわたることからも分かる。特に数論への貢献が大きく、1801年に発表された「ガウス整数論」をもって今日の「数論」という分野が誕生したとされている。発表はしなかったものの解析学でも時代を数十年を先んじた研究を行っていた。まだ複素数が市民権を得ていなかったが、20歳の頃には今日用いられている形式で複素平面(ガウス平面)を論じていた。その結果、アーベルによって世に発表される30年前にすでに楕円関数を発見していたという。
1801年、天文学者達はケレスと呼ばれる小さな新惑星の発見に沸いていたが、太陽の向こう側の軌道に入ってから見つけることができなくなってしまった。このころの天文学者はただ望遠鏡を向けるだけで、軌道を予測する数学的手法をもっていなかったのである。そこに、24歳のガウスが登場して数学的に軌道を予測した結果、ケレスは難なく見つかった。数学者には既に知られた存在であったガウスはこの発見によって科学界の寵児となった。また、この偉業は科学が急速に発展し始めた時代において数学が持つ予測能力を象徴したものとなった。この功績によりガウスはゲッティンゲン天文台長に就任し、終生そこに勤めた。以降、物理学とりわけ電磁気学における重要な発見をいくつも成し遂げ、1855年に77歳の生涯を閉じた。
素数の配列の謎
試しに、10000から10100までの素数を書き出すと次のようになる。
10007 10009 10037 10039 10061 10067 10069 10079 10091 10093 10099
差が2ですぐに素数が出てきたと思えば、20以上素数が出てこないなど素数の並びには全く規則性が感じられない。オイラーは「素数の並びには必ず意味があり、自然や宇宙と関係があるはずだ」という強い信念を持ち、素数の規則性を探すために次々に素数をあぶりだしていった。しかし、5万を超えても一向に規則性が表れる気配はない。そんなオイラーに対し周囲は冷ややかだった。多くの数学者は、素数は何の意味も持たない単に無秩序な数だと考えていたのである。しかし、オイラーはそんな批判を一気にはねのける発見をすることになる。
オイラーが解決したバーゼル問題と素数の結びつき
バーゼル問題とは、「平方数の逆数の無限和を求めよ」という問題であり、1644年に提起された。スイスのバーゼル在住のベルヌーイが挑んだものの解決できず、そのまま後世に託した問題であるためバーゼル問題と呼ばれるようになった。この入試問題はまさにバーゼル問題に対する解答を与えたものである。バーゼル問題は1735年にレオンハルト・オイラーによって解決された。ただし、その方法はこの入試問題の誘導とは異なる。わずかに高校範囲を超えてしまうがオイラーがとった方法を簡単に紹介しよう。
sinxは、マクローリン展開(大学1年で学習)により、次のような無限和で表される。(これはこれで驚きだが)
両辺をxで割ると
一方、sinx/xを別の形で表すことができる。sinx/xは、x=±π、±2π、±3π、……を代入するとsinx/x=0となるから、次のように因数分解できる。「f(x)にx=α、βを代入して0になるとき、f(x)が(α-x)(β-x)つまり(1-x/α)(1-x/β)を因数にもつ」と同様である。ここで、有限の話が無限の場合にも成立するかという問題が生じるがとりあえず無視する。
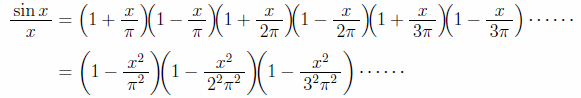
ここで、2通りに表されたsinx/xのそれぞれの式のx2の係数を取り出して等式を作ると
両辺に-π2を掛けて
このように少し乱暴ではあるものの、オイラーは非常に強い直感力と洞察力で2乗の逆数の無限和が(円周率の2乗)÷6に一致することを初めて発見したのである。オイラーはこのときのことを「エレガントな公式が見つかった」と記している。驚くべき結果だ。2乗の逆数の和を無限に足したものが円周率で表される値と完全に一致するというのだ。
オイラーの凄いところは、この結果に満足せずにさらなる追求を続けたところである。オイラーは以下に述べるようにして、左辺の無限和を書き換えられることを発見した。
例として、次のように分母が素数の2と3と5であるような無限和の積を作成して展開してみると、2と3と5で作られる全ての合成数の逆数の無限和ができる。分母に2、3、5以外の素数(7,11,13・・・)やその合成数が表れることはない。
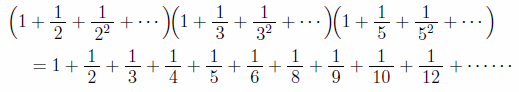
ここで、左辺の1つ1つの括弧内は無限等比級数(数Ⅲ)であるから、次のように変形できる。
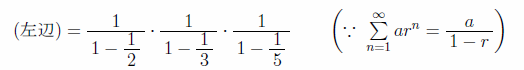
これを一般化し、全ての素数の無限和の積を作成して展開すると、全ての自然数の逆数の無限和ができることにオイラーは気付いた。この素数のみで作られた積をオイラー積という。
つまり、全ての自然数の逆数の無限和は全ての素数だけの数列の無限積で表すことができるのである。同じことを2乗で行えば
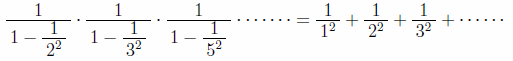
結局、先の結果と併せると次の等式が成立する。
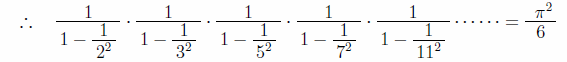
左辺は無限に存在する全ての素数を1つ残らず用いて作られた式である。全く規則性が見えなかった素数だが、全て集めてみると自然界で最も美しい形である円を表す円周率が表れるのだ。かくして、オイラーは円周率πを介在することで、素数の中に何らかの調和性があること、自然と素数が全くの無関係ではないことを人類史上初めて示した人物となったのである。
ガウスが発見した素数定理
オイラーに続いて、素数に隠された規則性に気付いたのは19世紀最大の数学者ガウスである。ガウスもまた素数の配列には何らかの意味があるはずだと考えていた。しかし、長年にわたって多くの数学者が素数の生成公式を見つけようとしては失敗してきたという事実から、そろそろ別の観点から考えてみてもよいだろうと当時15歳の少年ガウスは考えていた。
この前年、ガウスは人から対数表と素数表の両方が載っている本をもらっていた。計算機がない時代、商人や航海士は当たり前のように対数表をもっていた。莫大な数の計算が容易になり役立つからである。一方で、普通の人にとって素数表は実生活には応用できない無意味なものであった。しかし、ガウスが虜になったのは素数表のほうだった。対数の動きが予想できるのに対し、素数の動きは不規則だった。ガウスは素数が表れるタイミングを正確に予測しようというこれまでのアプローチを止め、ある特定の範囲内の素数の個数を予想できないかと考えた。素数が存在する割合を調べていったガウスはそれが対数表と関連していることに気付いた。1792年、15歳のガウスは1から自然数xまでの数の中に存在する素数のおおよその個数が次の式で与えられることを発見した。この「素数定理」が証明されたのはガウスが予想してから100年以上経過した1896年のことであった。ここで、π(x)は素数の個数を意味するものであり、円周率のπとは無関係であることに注意して欲しい。
対数は自然界にも頻繁に現れる。銀河や台風やアンモナイトなどに見られるような渦巻きは対数螺旋(極座標表示 r=aebθ)と呼ばれるものである。素数定理は、素数の個数がπと並んで自然界における重要な定数である自然対数の底eと密接に関係していることを示唆する。ガウスは自然対数の底eを介在することで、自然と素数が関連していることに気付いたのである。素数が自然界における2大定数円周率πと自然対数の底eに関連しているという事実は、素数が自然界の重要な構成要素であることを示唆している。
世界で最も美しい等式
ガウスが素数と自然対数の底eの関連性に気付く45年前、オイラーは円周率πと自然対数の底eの不思議な関係式を発見していた。このオイラーの公式と呼ばれる等式は、π、e、iという別分野で誕生した定数を仲立ちとして指数関数と三角関数を結びつけるものである。
この等式にθ＝πを代入して=0とすると次の等式が得られる。別々の分野で独立に発見された5大定数、円周率π(幾何学)、自然対数の底e(解析学)、虚数単位i(代数学)、和の単位元0(足しても元の数が変わらない)、積の単位元1(掛けても元の数が変わらない)が非常にシンプルにまとまっており、「世界で最も美しい等式」とも評されている。
自然界に潜む2大定数のキングπとクイーンeは、i(愛)で結ばれていたのだ。
未解決問題 リーマン予想
あのガウスを師にもつベルンハルト・リーマン(ドイツ ; 1826～1866)は、素数の研究を行う過程でオイラーが研究していた以下の級数を複素数全体にまで拡張し、ζ(ゼータ)関数と名付けた。s=(整数)を考えていたオイラーに対し、s=(全ての複素数)で考えることにしたのである。
このゼータ関数のゼロ点(ζ(s)=0となるような複素数s)が素数の並びと関連していることに気付いたリーマンは、自明なゼロ点(負の偶数)以外のゼロ点の位置を求め始めた。4個ほどゼロ点を求めてみると、複素平面において全てが一直線上(実部が1/2)に並んでいた。このとき、リーマンは完全に無秩序に散らばっていた素数がゼータ関数というフィルターを通して見ると高い秩序を保った姿に変わることに気付いたのだ。この4つのゼロ点だけが偶然並んでいるわけではなく、無数にあるゼロ点が全て一直線上にあるはずだという予想がいわゆる「リーマン予想」である(1859年)。
リーマンの功績は「素数の配列に規則性はあるか」という漠然とした問いを「自明でないゼロ点は一直線上にあるか」という数学の問題に帰着させたことにある。この問題はリーマンの予想から150年以上経過してもまだ未解決のままであり、数学における最重要問題の1つとなっている。コンピュータを用いてゼロ点を10兆個まで求めても全く反例が見つからないことから、多くの数学者は正しいと信じており、既にリーマン予想が正しいという仮定の下数千の論文が発表されている。
リーマン予想と量子物理学とのつながり
ヒュー・モンゴメリーはリーマン予想とは別の問題の解決のために、ゼロ点の間隔に着目し調べ始めた。当初、素数が無秩序であるのと同様、素数で作られるゼータ関数のゼロ点の間隔も無秩序であるはずだと考えていた。ところが、実際に調べてみると予想に反してゼロ点の間隔は完全に均一に散らばっているようだった。モンゴメリーは、間隔の分布をグラフにしてみたが、予想とは正反対の結果にその意味をとらえきれずにいた。
1972年、プリンストン高等研究所に立ち寄ったモンゴメリーは物理学者フリーマン・ダイソンと話す機会を得た。それは研究所で日常になっているティータイムの間の軽い会話のはずだったが、モンゴメリーがゼロ点の間隔を表す数式について話し始めたとき、ダイソンの顔つきが変わった。
数の原子ともいえる素数の間隔と自然や宇宙を構成する原子がもつエネルギーの間隔には密接な関連があったのだ。この2人の奇跡の巡り合わせは神から人類への贈り物であったのだろうか。人類は素数と自然界との真に深いつながりを発見した。リーマン予想の証明にもつながる素数の謎は、もはや数学者だけの挑戦ではなくなり、物理学者も含めて人類が力を結集して解明すべきものになったのである。
人類は素数と共に
リーマン予想に対しては、2000年にアメリカのクレイ研究所によって100万ドルの懸賞金が懸けられた(ミレニアム懸賞問題)。かつて、素数は物好きな人間の好奇心の対象でしかなく、実際には何の役にも立たないと考えられていた。しかし、今やインターネット通信の安全性が巨大な素数を用いた暗号によって保証されているように、素数は我々が暮らす現代社会と切っても切り離せいない関係になっている。リーマン予想が証明されるとき人類はまた新たな一歩を踏み出すことになるのかもしれない。
少し長いが、要はある自然数に対し「偶数なら2で割る」「奇数なら3倍して1足す」を繰り返すといずれは1になるというものである。問題文中では10の例が示されているが、(1)を実際にやってみると次のようになる。
6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1 より F(6)=8 (10の後は問題文と同じ)
11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1 より F(11)=14 (結局10の後は同じ)
自然数次第で1になるまでに必要な回数はかなり上下し、例えば27や31は100回以上の操作が必要になる。
未解決問題 コラッツ・角谷予想
問題文中では105以下の自然数とあるが、コンピュータの発達と共に記録が伸び続けており少なくとも3×253までは反例がないことが確かめられている。1937年、コラッツ(ドイツ)は「全ての自然数はこの操作を繰り返すと有限回の操作で必ず1に到達する」と予想した。これは、2013年現在未解決であり、あくまでも予想にすぎない。一見すると、大学入試にも出題されそうなくらい簡単に思えるこの問題が未だ世界のどんな天才数学者をもってしても解決できていないのである。
その他の未解決問題
数学の未解決問題は多くあるが、特に数論(整数)分野の未解決問題は中学生でも理解できるものが多い。その中から特に有名なものをいくつか取り上げよう。
「双子素数(差が2である2つの素数の組)は無限にあるか」 (3,5),(5,7)など
素数が無限にあることは、紀元前には世界三大数学者ユークリッドによって証明されていた。また、差が2である3つの素数の組は(3,5,7)のただ1組しか存在しない。このことは大学入試問題として適度な証明問題であり、次の早稲田大学(2004年)の問題が有名である。
簡潔に証明しておく。n=3kのときn=3k=(3の倍数),n=3k+1のときn+2=3k+3=(3の倍数)、n=3k+2のときn+4=3k+6=(3の倍数)より、(n,n+2,n+4)のうちどれか1つは必ず3の倍数となる。よって、素数の中でただ1つ3の倍数である3を含む(3,5,7)の場合しか存在しない。(1は素数ではないので1,3,5はダメ)
このように、素数が無限にあることと差が2である3つの素数の組が1組のみであることはわかっているのだが、「双子素数が無限にあるか」は未解決の問題である。なお、1組しかない(3,5,7)を三つ子素数としても面白くない。そこで、(p,p+2,p+6)または(p,p+4,p+6)と表せる3つの素数の組を三つ子素数という。例えば、(5,7,11)や(7,11,13)などがある。
2014年4月追記：双子素数の問題は古代ギリシャ時代から2000年間あまり進展がなかったが、2013年大きく進展した。2013年5月、「差が7000万以下の素数の組が無限に存在する」ことが示された。差が2と差が7000万では大きな違いがあるが、差が無限から有限の7000万という定数になった意義は大きい。新たな着想による1つの発見を突破口にして一気に研究が進展しても不思議ではない。実際、半年後の2013年11月には「差が600以下の素数の組が無限に存在する」ことが示された。これを「差が2以下」にまでできるかが注目されている。
ゴールドバッハ予想 「4以上の全ての偶数は2つの素数の和で表せる」
例えば4=2+2、6=3+3、10=3+7=5+5のように、偶数を2つの素数の和で表すことを考える。これが全ての偶数で可能だと予想するのがゴールドバッハ予想である。コンピュータによって少なくとも5×1017までは確かめられている。
「偶数の完全数は無数にあるか」「奇数の完全数は存在するか」
完全数とは「約数の和(その数自身は除く)が自身に等しい自然数」のことである。例えば6の約数は1,2,3,6だが、6以外の和が1+2+3=6となり6自身に等しいから、6は完全数である。同様に、28の約数は1,2,4,7,14,28で、和が1+2+4+7+14=28であるから28も完全数である。完全数については紀元前から考察対象になってきたが、「完全数は無数にあるか」や「奇数の完全数はそもそも存在するのか」といった問題は未解決である。
「メルセンヌ素数は無数にあるか」
メルセンヌ素数とは「Mn=2n-1」で表される素数のことである。1644年、マラン・メルセンヌは「Mnが素数となるのは257以下の自然数ではn=2,3,5,7,13,17,19,31,67,127,257のときのみである」と主張した。しかしこれは誤りで、n=67,257のとき合成数となり、またn=61,89,107のときにも素数になることがわかっている。n=67のときに素数となるという予想は250年以上反例が示されなかったが、1903年フランク・ネルソン・コールがアメリカ数学学会において一言も言葉を発することなく黒板に「M67=193707721×761838257287」と書いて席に戻ると、しばらくして拍手が沸き起こったという。
現在、コンピュータによるメルセンヌ素数探しのプロジェクトGIMPS(Great Internet Mersenne Prime Search)により次々と新しい超巨大素数が見つかっており、発見される素数の桁数は1000万桁を超えている。近年発見された巨大素数は全てメルセンヌ素数である。これは、メルセンヌ素数に関しては素数か否かを判定する効率的な方法が発見されているからである。このメルセンヌ素数が無数にあるかという問題は未解決である。
数学者にとっては悪夢？コンピュータで証明された四色問題
四色問題とは「任意の地図が4つの色で塗り分けできるか」という問題である。地図を製作する際には塗り分けが必要になるので、数百年前から経験的に知られてはいたが、そのことの数学的な証明はなかなかなされず未解決の時代が続いた。ところが、1976年になって膨大な場合分けをコンピュータに任せることで考えられ得る全ての場合が尽くされた。未だコンピュータを用いない証明は得られていない。コンピュータを使った証明をどう扱うかは意見が分かれそうなところである。コラッツ・角谷予想を含め、上で取り上げた予想は多くの数学者がそれなりの根拠を元に正しい予想だと考えているが、もしかするとコンピュータによって反例が見つかる日が来るかもしれない。
同種の問題は毎年どこかの大学で出題されるが、わざわざ問題文の中でフェルマーの最終定理に言及しているところがおもしろい。この前置きは問題を解く上で何の必要もない無駄な記述である。それをわざわざ書くということは、問題作成者にとって何かこだわりがあったのだろうか。あるいは、「数学では成り立つことが確定している命題を成り立たないと仮定した場合に何が起こるかを追求することが可能である」ことを示唆しようとしているのだろうか。実際、このフェルマーの最終定理が証明される過程において、「もし整数解が存在するとしたら解はどんなものなのか」を追求することで大きな進展があった。これにちなんだ出題なのかもしれない。
指数部分が2、つまり三平方の定理の形x2+y2=z2の場合は、全て3の倍数と仮定し整数を3で割った余りで分類して両辺の余りの不一致によって矛盾を導く(背理法)ことで証明するという整数分野の基本問題である。この問題(3乗)の場合、結局9で割った余りで分類することで同様に証明できる。解答は簡潔に示しておく。
伝説の数学者フェルマーの遺言と数学者の初期の試み
x2+y2=z2を満たす自然数(x, y, z)の組は(3, 4, 5)など無数に存在することが知られている。ところが、フェルマーは指数を3以上にするとそれを満たす自然数(x, y, z)の組が1つも存在しなくなってしまうというのである。17世紀、フェルマーは「この定理に関して私は真に驚くべき証明を見つけたが、この余白はそれを書くには狭すぎる。」と書き残して亡くなった。フェルマーが残した多くの予想は後の数学者によって1つずつ解決されていった。しかし、この予想だけは解決されないまま残った。そのため、この予想は「フェルマーの最終予想」と呼ばれるようになった。
長い間、特殊なnについての場合を個別に証明しようとする試みが続いた。元々、例えばn=3のときが証明されれば3の倍数のときが証明されたことになるので、結局はn=4の場合とn=素数の場合を証明すればよいのである。特定のnのときに証明されるなど少しずつは進展したが、根本的な解決がなされないまま300年という時が流れた。その間、無数の数学者が中学生でも理解できるこの命題の魔力に惹かれ挑戦したが、全員が敗れ去っていったのである。
証明の必要性
フェルマー予想については20世紀までに、膨大な計算が必要ではあるが理論上は個別のnの場合を1つずつ処理できることが示されていた。そこにコンピュータが登場し小さいnの場合から次々に確認することが可能になった。1950年頃にはn=500まで証明され、その後n=400万までが証明された。しかし、素数は無限にある。仮にコンピュータを用いてあるnまでの場合を全て証明したところで無限のnについて証明されることは永遠にないのである。証明のない予想がどれほど危ういものなのかを示す例をいくつか挙げよう。
この数列は一見するとずっと素数が続くようにも思えるが、実際に確かめてみると8番目で素数ではないものが出現する。
他にも見てみよう。18世紀最大の数学者オイラー(スイス)は、フェルマー予想をさらに拡張した次の方程式には自然数解がないと予想した(オイラー予想)。
この予想は200年の間証明もされず反例も見つからなかった。さらにコンピュータが数年がかりで調べても見つからなかったので、正しい予想であると考えられるようになっていたが、1988年になって次の解が発見され、オイラー予想は否定的に解決された。しかも、無数の解があることまでが証明された。
次の例には恐怖すら覚える。18世紀末、当時15歳だったガウス(19世紀最大の数学者;ドイツ)は、素数の分布を予想する式を与えた。この式はかなり正確だったが、常に実際よりもわずかに多めの値が得られた。1兆まで調べても常に多かったので、数学者はこの傾向が無限に続くと考えていたが、1955年にスキューズ(南アフリカ)が下に示した数(スキューズ数と呼ばれる)の少し手前で予想を下回ることを示した。これは想像を絶する大きさの数であり、宇宙に存在する全素粒子数1088＜10102をもってしても比較対象にすらならない。当時は「数学的意味を持つ最大の数」であった。現在はグラハム数のように10進法では記述することすら出来ないほど巨大な数が考察対象となっているようである。
これらの例でわかるように、どんな大きな値まで調べたとしても、証明がない限りは予想はあくまでも予想にすぎないのである。
ゲーデルの「不完全性定理」
証明に関しては、もう1つ面白い話がある。1931年、数学者クルト・ゲーデルが示した不完全性定理は数学者達に大きな衝撃を与えた。数学者達は「数学体系は一切の矛盾がない完全なものであり、いかなる命題も真偽が判断できる」ことを当然のように信じて疑っていなかった。しかし、ゲーデルは「数学が完全ではなく、数学的に証明も反証も出来ない命題が存在する」ことを数学的に証明してしまったのである。これは有名な嘘つきのパラドックス「私は嘘つきだ」を焼き直した次の命題でたとえられる。
「この命題は証明できない」
もしこの命題が偽だとすると証明できることになるが、証明できないというこの命題自身に矛盾する。また、真だとすると命題自身が述べるように証明できないことになる。ゲーデルはこの命題を定式化することで真であっても証明不可能な問題が存在することを示した。フェルマー予想に取り組んでいて不完全性定理を知った数学者達が「もしかしたらフェルマー予想はそもそも証明不可能なのかもしれない」と考え始めたとしても何ら不思議なことではないだろう。
谷山＝志村予想からアンドリュー・ワイルズ(イギリス)による最終証明まで
1955年、谷山豊と志村五郎は「全ての楕円曲線はモジュラーである」と予想した。楕円曲線とモジュラーは全く別分野の概念であるが、それが同種のものだというとてつもない予想である。これを「谷山＝志村予想」という。発表当初は全く信用されなかったが、志村が積み上げた証拠のおかげで広く信じられていった。現代数学において計り知れない重要さを持つ予想であり、谷山＝志村予想の証明が数学界の最大の目標の1つとなった。証明はされていなかったにもかかわらず、谷山＝志村予想が正しいという仮定のもと20年間で数百の論文が発表された。もし、谷山＝志村予想が間違っていた場合それらの論文は全てゴミとなる。数学者達は、誰かが証明し土台を確固たるものにしてくれることを渇望していた。
1984年、ゲルハルト・フライ(ドイツ)はフェルマー予想がもし間違っていたら、つまりもし仮に解を持つとしたらどうなるのかと考え仮想的な解を代入していった。するとモジュラーではない異常な楕円曲線が現れた。これは谷山＝志村予想に反することになる。つまり、「フェルマー予想が偽ならば、谷山＝志村予想も偽である」ことを意味する。これを逆に考えると、「谷山＝志村予想が真ならば、フェルマー予想も真である」となる。この瞬間、フェルマー予想の証明は谷山＝志村予想の証明に移り代わったのである。
ワイルズは10歳の時にフェルマー予想を知り、自分が証明することを夢見て数学者になった。子供の頃の夢は封印して現代数学の主流である楕円曲線を研究をしていたが、自分の専門分野である楕円曲線がフェルマー予想と結びついたことで、全ての研究を止め谷山＝志村予想の証明に自分の人生を賭けることにした。その後7年間自宅の屋根裏部屋にこもり、フェルマー予想の証明に没頭した。
予想から350年以上経過した1995年、ついに最終決着がなされた。ワイルズがフェルマーの最終予想を完全に証明したのである。フェルマーの最終予想はもはや予想ではなくなり、フェルマーの最終定理となった。後にアメリカ数学界がこの完全証明に重要な役割を担った十数名の功労者を挙げたが、その中の6人が日本人であった。
エドワード・フレンケル教授の講義は佳境に入ってきた
1955 年、日光で開かれた数論の国際学会で日本の数学者谷山豊が得た着想は、「奇跡」とも言えるひらめきだった。その着想とは、非常に複雑な数論の問題を、調和解析というまったく別の数学を使って解くことができるというもの。この「谷村・志村・ヴェイユ」予想が、後に数学史上最大の難問と言われた「フェルマーの最終定理」の解決につながってくる。そのドラマチックな展開をフレンケル教授の著書『数学の大統一に挑む』の訳者である青木薫が読み解く。
NHK Eテレ『数学ミステリー白熱教室』の第3回は、「夭折した日本の数学者が、数学の大統一に果たした役割」だった。ラングランズ・プログラムの核心に迫り、「数論と調和解析の不思議なつながり」を探ることがテーマだった。フレンケルは、簡単な例を見てもらうことで、数学の異なる分野がつながるとはどういうことなのかを感じ取ってほしいという。
そんなつながりを示すうえで重要な役割を演じたのが、かの有名な「フェルマーの最終定理」だ。その「定理」は、一見するとピタゴラスの定理を素直に拡張しただけのようのようにみえる。ところが、なんのことはなさそうなその問題が、実に350年以上ものあいだ、未証明のままにとどまったのである。
フェルマーの最終定理
未証明なのだから「定理」ではなく、「予想」と呼ばれるべきだったろう。しかし、1637年頃にこの問題について考えたピエール・ド・フェルマーは、証明を発見したと考え、「真におどろくべき証明を見つけたが、余白が狭すぎるので、ここに書くことはできない」という有名な台詞を残して死んでしまった。
上記の式でn が3以上の自然数の場合X、Y、Zを満たす整数解はない」がフェルマーの最終定理
多くの数学者を魅了し、多彩なエピソードに彩られた「フェルマーの最終定理」は、もともと数論の未解決問題だった。ところが1985年のこと、「フェルマーの最終定理」は、「志村・谷山・ヴェイユ予想」という別の予想の特殊ケースであることが示されたのである。つまり、「志村・谷山・ヴェイユ予想」が証明できれば、自動的にフェルマーの最終定理を証明したことになるのだ。
こうして一挙にスポットライトを浴びた「志村・谷山・ヴェイユ予想」だったが、実はこの予想は、ラングランズ・プログラムにとって重要な意味をもっていた。それは、数論と調和解析とをつなぐ驚くべき予想だったのだ。
フレンケルは、この連続講義の最初にラングランス・プログラムとは何かを説明する際に、崩したジグゾーパズルの山をいくつかつくり、「数学にはさまざまな領域がある。それらはいわば海に隔てられた大陸のようなものだが、しかしそこには不思議なつながりがある。そのつながりを探っていくこと」と説明した。
「数論」と「調和解析」
調和解析の例
数論とは、数の性質とふるまいを探る世界、調和解析とは、たとえば三角関数や音の倍数など周期を起点にして考える数学だ。
一見似ても似つかない二つの分野が、どう関係しているのか。
フレンケルは鮮やかにそのことを講義する。数論の分野では手に負えなかった難問が、調和解析の世界に持ち込んだとたん、鮮やかに解けてしまう。
それが、「志村・谷山・ヴェイユ予想」だと。
何のパターンもなさそうに見え、このままでは、まるで泥沼にはまったように、どこまでも先の見えない計算を続けることになりそうな数論の問題が、特殊な対称性を持つ調和解析の関数を考えることで、すっきりと解決しまう。
そして、この予想を証明することが、数学者たちの挑戦を300年以上にもわたって退けてきた、「フェルマーの最終定理」を証明することになったのだと。
フレンケルの講義を聞きながら、わたしは背中がゾクッとした。これは魔法じゃないか。たった一行の式が、まるで打ち出の小槌か、魔法の杖のように思われた。その式をちょっと振ってやれば（カッコをはずせば）、泥沼のような数論の問題への答えが、ポロポロと出てくるのだから。
さて、今回の講義では、「志村・谷山・ヴェイユ予想」という予想に貢献した日本の数学者について、フレンケルは感動的に語っている。
夭折した日本の数学者 谷村豊
そう、夭折した日本の数学者、谷山豊が登場するのだ。谷山は、この予想を1955年に日光で行なわれた数論の国際学会の最中に着想しながら、その三年後に自殺してしまう。志村が谷山のアイデアを発展させきちんとした形にし、ヴェイユがそれを広めたのだ。
人間の洞察と閃きの深遠さ
フレンケルは、「志村・谷山・ヴェイユ予想」を奇跡と表現し、「コンピュータがどんな複雑な演算をこなすようになっても、人間の洞察と閃きの深遠さにはかなわない」。その驚きの瞬間がこの予想にはあると語った。
エドワード・フレンケル（Edward Frenkel）／1968年旧ソ連生まれ。父親がユダヤ人との理由でモスクワ大学の入学試験で全問正解したにもかかわらず不合格となり、やむなく石油ガス研究所（日本でいうところの工業大学）に入学、応用数学を学ぶ。一方で純粋数学の研究を続け、在学中にハーバード大学に客員教授として招かれる。その後、ラングランズ・プログラムと出合い、量子物理学にまで拡張。カリフォルニア大学バークレー校の数学教授。親日家でもある。「愛の数式」をテーマとする映画を製作・出演
そして、「数学者は人間なのだ」とフレンケルは強調するのだ。親友である谷山の早すぎた死を深く悲しむ志村五郎の言葉を引きながら、「数学者は人間なのだ」と。
フレンケルはそう学生に語りかけながら、一瞬絶句する。そんなフレンケルの様子を見ながら、わたしは今から15年ほど前に、志村先生と直接お会いした時のことを思い出していた。
サイモン・シンの『フェルマーの最終定理』の翻訳をしていたときのこと、プリンストンの志村先生と少しメールでやりとりをし、さらに集中講義のために京都大学にいらした際には直接お会いする機会を得たのだった。
今から述べるのは、そのとき（本題を離れて、完全にオフレコ気分の雑談のとき）に出た話題である。そんな会話をこのような場に書いてよいものか少し悩んだが、書いてはいけないと考える積極的理由もないように思うので、書くことにする（志村先生、お許しを！）。
わたしは志村先生に、ロバート・ラングランズをどう評価なさるかとお尋ねした。すると先生はさらっと、「（ラングランズは）旗振りしただけでしょう」とおっしゃったのだ。ここで急いで補足するが、時代に先駆けて立ち上がり、旗を振るというのは誰にでもできることではない。
フレンケルの今回の講義でも、もしかするととんでもない大間違いかもしれない洞察を述べることへのラングランズの不安が、ヴェイユに宛てた手紙（実質的には論文）への添え書きに、はっきりと表れていた。旗を振ることは、それはそれ自体として、すごいことなのだ。
ラングランズに対する志村先生の評価は、志村先生ご自身の数学との向き合い方、あるいは数学観のようなものと密接に結びついているはずのものである。このコメントは、志村先生の口から出たからこそ凄みがあるのであって、そんじょそこらの者が口にすれば、薄っぺらなセリフにしかならないだろう。
とはいえ、わたしが強い印象を受けたのは、ラングランズについての先生のコメントではない。わたしはそれに続けて、「では、ヴェイユはどうですか」とお尋ねした。すると先生は、一瞬間をおいてから、ひとことひとこと区切るように、力を込めてこうおっしゃったのだ。
ヴェイユは数学界における一等星
「ヴェイユは、まぎれもなく、一等星でした」。つまりヴェイユは、数学史上に燦然と輝く一等星のひとつだというのだ。わたしの目と耳には、このときの志村先生が焼き付いている。この先生の言葉の重みを自分のものとして実感することは、数学者ならぬ身のわたしには永遠にできないだろう。けれども、今でも翻訳の仕事でヴェイユに出会うと、この人は志村先生にあのように言わせた人物なのだと、襟を正してしまうのである。
白熱教室の講義をより深く理解するための一冊
実はこのとき、わたしはさらに続けて、「では、志村先生ご自身は何等星でしょうか？」とお尋ねしたのだが、この問いに対する先生の答えは、みなさんのご想像にお任せすることにしたい。
フレンケルの著書『数学の大統一に挑む』は、大勢の数学者たちを糸として織りなされるタペストリーのようなものと見ることができる。ロバート・ラングランズとアンドレ・ヴェイユは、全体のトーンを決める重要な2本の糸だ。
そこに意外な方面から、第3の重要な糸が現れる－－物理学者エドワード・ウィッテンである。
さて「数学ミステリー白熱教室」次回はいよいよ最終回。そのテーマは「数学と物理学 驚異のつながり」だという。はたしてウィッテンは、講義にも登場するのだろうか？ だとしたら、フレンケルはこの驚くべき人物をどのように語るのだろう？ 最終回となる第四回は、フレンケル自身にとっても格別のクライマックスとなるはずだ。