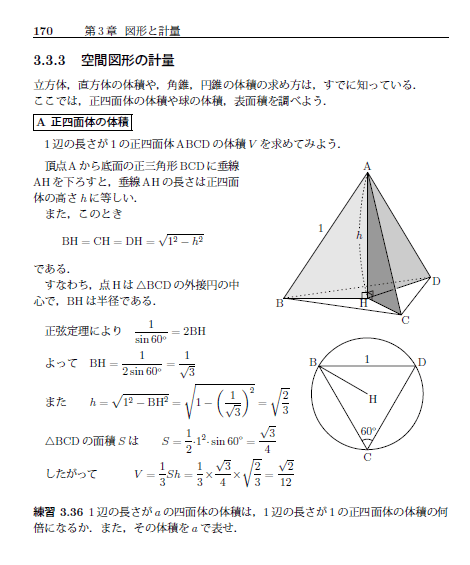
フェルマーの小定理

フェルマーの小定理

合同式の「100乗問題」を扱った際に、「1」を探すのがコツという話がありました。このようなケースで、累乗しながら「1」を探していくと、ある規則性がみえてきます。それが「フェルマーの小定理（Fermat's little theorem）」 と呼ばれるもので、合同式の関連では最も有名な定理です。

 

フェルマーの小定理は上のような格好をしています。法の割り数が素数 （prime number）であり、累乗元の基数とも「互いに素」であれば、法より1小さい乗数のところで余りが必ず１になる、という内容です。値を入れ替えながらいくつか実際に見てみましょう（電卓の用意をどうぞ）。

確かにそうなっています。今度は累乗元の数を固定して、「法」の素数の方をずらしてみましょう。

成立していますね。100乗問題でみたテクニックとともに、この「1」は使えます。この定理を使うと、たとえば次のような問題が剛速球で解けます。

もういっちょういきましょう。

「フェルマーの小定理」の「フェルマー」は、あの有名な「フェルマーの最終定理」と同じ、スーパースター数学者のフェルマーさんです。没後にノートの書きつけが公表されて以来、300年以上誰にも解けず、もともと解けないのでは、と言われていたところ、1995年に証明法が解明されて大騒ぎになった「最終定理」と区別するために、こちらの合同式に関する定理は「小定理」と呼ばれています。「最終～」とちがって、こちらの方の証明はそれほど難しくないそうなので、この場所でものちほどチャレンジしてみます。

フェルマーの小定理と循環小数

ところで、この小定理で、累乗元の数の方を固定した上の検証において、基数を「10」にとってどうなるかをみてみます。

すると、左側の、余りを引いて割った「商」の部分に、なにやら見たことのある数が出てきました。そう、これは循環小数（純・循環小数）の循環節の数です。

「10の累乗に対して1余る数」というのは、「9999...」の数を割り切れる、ということと同じですから、フェルマーの小定理は、循環小数の組成と深くからみ合っています。

上の例でみると、「mod 7」ではナマの循環節そのものが現れていますが、他のケースでは循環節の繰り返しが出ています（「13」のケースでは「076923」が2回繰り返されています）。ここから、次のふたつのことを読みとることができます。

• フェルマーの小定理は余りが1になる乗数を指示するものではあっても、循環節を作るその「最短」の乗数を示すものではない
• 循環節を作る「最短」乗数はフェルマーの小定理が指定する乗数自身かその「約数」のどれかになる

上の例では、「mod 11」のときに10の2乗、「mod 13」では6乗で最短で1と合同となり、これが循環節になります。このカタマリをまるごとさらに累乗したものも余り1ですから、指数を整数倍したそのどこかが小定理の要求する乗数にヒットするという構造です。

純・循環小数の循環節の長さを順々に調べていくと、対応する分数の分母（割り数）の素数から1小さい数とその1/2などの約数が並ぶ様子が観察できます。この土台にはフェルマーの小定理があります。合同式の剰余演算と循環小数が底のところで深くつながっていることがよく分かりますね。

京都大学・理系・文系・数学・空間図形・正四面体 61（さくら教育研究所）

＜京都大学・理系・数学・空間図形・正四面体＞ 

＜コメント＞

京大でよく出る「中学生から解ける」図形問題です。（過去問の研究）

教科書の練習問題から丁寧に解いてますか？

地に足の着いた勉強をしてますか？

背伸びして難問ばかり追い求めてませんか？

・・・（数学の発想のしかた）

＜参考：さくらの高校数学の教科書＞

＜2016年・京都大学・文系・数学・空間図形・正四面体＞ 

＜コメント＞

理系の「外心」が、文系では「重心」になっている。

どうして文系の方が難しいの？

理系の方は幾何で解けたのに、文系はベクトルなの？

・・・

＜参考：さくらの高校数学の教科書＞

＜参考：さくらの高校数学の教科書＞

さくらの個別指導（さくら教育研究所）

「ウィルソンの定理」とその証明

「ウィルソンの定理」とその証明

前回のフェルマーの小定理の証明では、階乗の計算は助っ人で来てもらって、用が済んだら最後は両辺から払って帰ってもらいましたが、この素数の余りから作った階乗の数自身が、除数の法に対してどういう関係にあるのかも、ついでに調べておきましょう。

 

例として、前回使用した、素数の 5 を法／除数とした場合のケースで考えます。余りはいくつでしょうか？

これを考える際に、左辺の階乗の計算を、次のように並べ替えることが参考になります。

こうすると、「4×1」は 4 で、法の 5 に対しては剰余「-1 （5-1）」です。また同様に、「3×2」は 6 で剰余「1 （5+1）」です。すなわち、全体の余りは「-1×1」で「-1」となります。

実は、法／除数が素数のときには、この並べ替えは常に行うことができます。頭のあたりでいくつかみてみましょう。

つまり、このパターンでは余りは常に「-1」になるということです。文章で書けば、法の素数に対して、それがとりうる余りで作った階乗は、余りが「-1」になる、となります。また、言い方を変えれば、この階乗の値は「+1」すると、法の素数で必ず割り切れる、とも言えます。この階乗と素数の剰余の関係を表す法則を「ウィルソンの定理」といいます。一般化した形で書くとこうです。

ウィルソンの定理は、フェルマーの小定理ほど有名ではなく、なんの役に立つのかもちょっとよく分からない内容ですが、小定理に劣らず美しい形ですし、素数と階乗というそれぞれ特殊な数ふたつを、剰余を仲立ちにつないでいる点で、純粋に数の性質や不思議さを楽しむうえでとても面白い性質といえます。素数は自分自身と1以外の約数を持たない数であり、階乗は逆に自分以下のすべての数を約数に持つ数です。このうち、階乗の側については、（P-1）より大きくしてしまうと、法の素数自身が入ってしまって割り切れてしまいますから、「自分の余りで作った」というところがミソです。

ウィルソンの定理が成り立つ原理

階乗と素数の間でこの性質が成り立つのは、上記のように、素数が法の場合には、階乗の中身を剰余が「-1×1」になる組み合わせに必ず並べ替えられることが前提になっています。なぜこれが成り立つのかは、前回のフェルマーの小定理の証明を応用することで理解できます。

フェルマーの小定理の証明では、素数の余りに「互いに素」の数をかけて作った合同式のセットは、余りがバラバラに1回づつ入る、という指摘が核になっていました。前回は、5 と 7 という数の組みでこれを確認しましたが、これは法より小さい数でもまったく同様に当てはまります。法／素数を「7」として、いくつかみてみましょう。

このケースでもたしかにそうなっていますね。これを仮に「ルール1」とすると、この合同式のセットには、他に次のいくつかの規則性が指摘できます。まずそのひとつは、この階乗のそれぞれの要素は、同じ余りの範囲の中で、掛け合わせると剰余が「1」になるペアーを必ず見つけることができる、というものです。これは「ルール1」を剰余の側からみて言い換えただけです。これを「ルール2」とします。また、（ａ）を変えながら、同じ行についてみると、剰余の「1」は必ず1度だけ出る（2度は出ない）、ということもいえます。これも「ルール1」を言い換えたもので、もし2度以上出るのであれば、フェルマーの小定理の証明でみたように、同じ因数を持つ合同式の間で割り算ができることになってしまいますので、矛盾が生じるからです。これを「ルール3」とします。

次に上図で、いちばん上の行と最後の行の「1」と「6」に注目します。この行では「ルール2」「ルール3」から、1度だけでる「1」の剰余は、それぞれ自分自身を掛け合わせたとき、すなわち「1×1」と「6×6」のとき、で決まっています。なぜかというと、「1」「6」はそれぞれ自分自身が既に剰余「1」と「-1 （P-1）」なので、剰余「1」を作る組み合わせはそれしかないからです。

これを残りの「2～5」についてみると、最上行と最終行については、既に「×1」と「×6」で「1」の目を使ってしまっていますので、（ａ）に「2～5」をいれたときに剰余が「1」になることはない、ということになります。これは裏返せば、真ん中の「2～5」の行において、剰余の「1」を作る相手側の候補に最初の「1」と最後の「6」が来ることはない、という意味です。これを「ルール4」とします。

さらに、この真ん中の「2～5」の行において、「1」「6」の行のときと同様に、自分自身と同じ数が来た場合のケースを考えます。実はこのパターンでは（「1×1」と「6×6」のときとは反対に）剰余に「1」の目が来ることは絶対にありません。なぜかといえば、もしこの場合に剰余が「1」であれば、以下の合同式が成り立つことになりますが、

これは変形して上のようになります。これはすなわち、「2～5」の行において、「+1」「-1」にずらした数を掛け合わせた数が素数「P」で割り切れることを意味しています。しかし、上記の階乗から作った合同式のセットで、最上行と最下行をカットした「2～5」の候補が「+1」「-1」にずらした範囲で（「2－1＝1」以外に）法の素数の因数になることはありえませんから、これはおかしい、ということになります（たとえば「mod 7」で「4×4」をそれぞれ「+1」「-1」にずらした「5×3」や、「2×2」をずらした「3×1」が「7」で割り切れることはない、ということです）。結局、この範囲で一度きり出る「1」の目は、同じ数が掛け合わさったパターンからははじかれることになります。これを最後の「ルール5」とします。

この「ルール1」から「ルール5」までを全部足し合わせると、この合同式のセットで、いちばん上といちばん下を取り除いた「2～5」の行は、剰余が「1」になるペアーを、それぞれが相手側も「2～5」の範囲で、自分自身以外に必ず見つけることができる、となります。残った最上行と最終行は互いに組み合わせれば必ず剰余「-1」ですので、これでウィルソンの定理が成立する前提がめでたく確保された、というワケです。

まるで参加した者はひとりも「壁の花」になどならずに、全員無事きれいにペアーに分かれるよう、素数という主催者があらかじめ仕組んでおいた心憎いダンスパーティーのようですね。

阪大・国語 51012 （大阪大学）（さくら教育研究所）