算額(その692)
神壁算法 關流藤田貞資門人 龜井隠岐守家士 堀田人助泉尹 天明八年
藤田貞資(1789):神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf
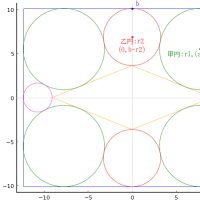
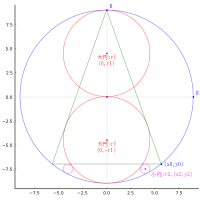
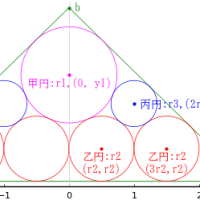
直径 97 寸 5 分の大円の中に累円と,大円と甲円と累円に挟まれる円がある。
末円の直径が 1 分のとき,初円から末円まで何個の挟円があるか(つまり,末円は初円から数えて何番目か)。
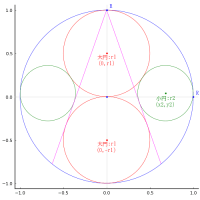
大円の半径と中心座標を r0, (0, 0)
甲円の半径と中心座標を r1, (x1, y1); x1 = 0, y1 = r1
乙円の半径と中心座標を r2, (x2, y2); x2 = r0 - r2, y2 = 0
乙円以降 i 番目の円の半径と中心座標を ri, (xi, yi)
初円の半径と中心座標を R1, X1, Y1
初円以降 i 番目の挟円の半径と中心座標を Ri, (Xi, Yi)
とおき,順次パラメータを決定していく。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms r0::positive, r1::positive,
r2::positive, x2::positive, y2::real,
r3::positive, x3::positive, y3::positive;
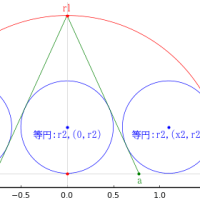
まず,乙円については,半径 r2 = r0/3 になる。
r1 = r0/2
x2 = r0 - r2
y2 = 0
eq1 = x2^2 + r1^2 - (r1 + r2)^2
res2 = solve(eq1, r2)
res2[1] |> println
r0/3
次に,丙円については,半径,中心座標は (r0/6, 2*r0/3, r0/2) になる。
r2 = r0/3
x2 = r0 - r2
y2 = 0
eq2 = x3^2 + y3^2 - (r0 - r3)^2
eq3 = x3^2 + (r1 - y3)^2 - (r1 + r3)^2
eq4 = (x2 - x3)^2 + (y2 - y3)^2 - (r2 + r3)^2
res3 = solve([eq2, eq3, eq4], (r3, x3, y3))
1-element Vector{Tuple{Sym, Sym, Sym}}:
(r0/6, 2*r0/3, r0/2)
更に,丁円については,半径,中心座標は (r0/11, 6*r0/11, 8*r0/11) になる。
@syms r4, x4, y4
(r3, x3, y3) = res3[1]
eq5 = x4^2 + y4^2 - (r0 - r4)^2
eq6 = x4^2 + (r1 - y4)^2 - (r1 + r4)^2
eq7 = (x3 - x4)^2 + (y3 - y4)^2 - (r3 + r4)^2
res4 = solve([eq5, eq6, eq7], (r4, x4, y4))
2-element Vector{Tuple{Sym, Sym, Sym}}:
(r0/11, 6*r0/11, 8*r0/11)
(r0/3, 2*r0/3, 0)
@syms r5, x5, y5
(r4, x4, y4) = res4[1]
eq8 = x5^2 + y5^2 - (r0 - r5)^2
eq9 = x5^2 + (r1 - y5)^2 - (r1 + r5)^2
eq10 = (x4 - x5)^2 + (y4 - y5)^2 - (r4 + r5)^2
res5 = solve([eq8, eq9, eq10], (r5, x5, y5))
2-element Vector{Tuple{Sym, Sym, Sym}}:
(r0/18, 4*r0/9, 5*r0/6)
(r0/6, 2*r0/3, r0/2)
@syms r6, x6, y6
(r5, x5, y5) = res5[1]
eq11 = x6^2 + y6^2 - (r0 - r6)^2
eq12 = x6^2 + (r1 - y6)^2 - (r1 + r6)^2
eq13 = (x5 - x6)^2 + (y5 - y6)^2 - (r5 + r6)^2
res6 = solve([eq11, eq12, eq13], (r6, x6, y6))
2-element Vector{Tuple{Sym, Sym, Sym}}:
(r0/27, 10*r0/27, 8*r0/9)
(r0/11, 6*r0/11, 8*r0/11)
@syms r7, x7, y7
(r6, x6, y6) = res6[1]
eq14 = x7^2 + y7^2 - (r0 - r7)^2
eq15 = x7^2 + (r1 - y7)^2 - (r1 + r7)^2
eq16 = (x6 - x7)^2 + (y6 - y7)^2 - (r6 + r7)^2
res7= solve([eq14, eq15, eq16], (r7, x7, y7))
2-element Vector{Tuple{Sym, Sym, Sym}}:
(r0/38, 6*r0/19, 35*r0/38)
(r0/18, 4*r0/9, 5*r0/6)
@syms r8, x8, y8
(r7, x7, y7) = res7[1]
eq17 = x8^2 + y8^2 - (r0 - r8)^2
eq18 = x8^2 + (r1 - y8)^2 - (r1 + r8)^2
eq19 = (x7 - x8)^2 + (y7 - y8)^2 - (r7 + r8)^2
res8= solve([eq17, eq18, eq19], (r8, x8, y8))
2-element Vector{Tuple{Sym, Sym, Sym}}:
(r0/51, 14*r0/51, 16*r0/17)
(r0/27, 10*r0/27, 8*r0/9)
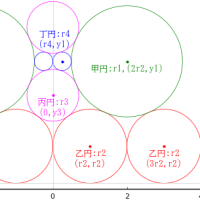
累円のパラメータ,半径,中心座標を表す数列には規則性があり,以下のような一般項になる。
甲円の半径 r1,中心座標 (x1, y1) は r0/2, (0, r1)
乙円の半径 r2,中心座標 (x2, y2) は r0/3, (r0 - r2, 0)
丙円以降は i ≧ 3 として,ri, (xi, yi) は以下のようになる。
ri = r0/(i^2 - 2i + 3)
xi = ri*(2i - 2)
yi = ri*(i^2 - 2i)
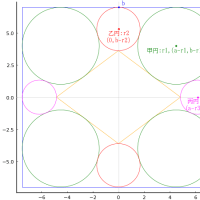
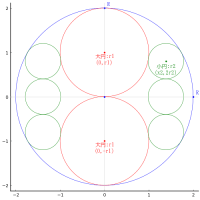
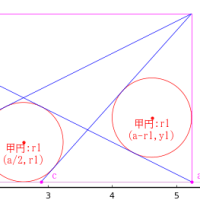
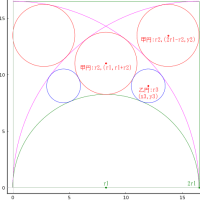
次に,互いに接する,外円と 2 個の累円に挟まれる円のパラメータを計算する。
@syms R1, X1
X1 = r0 - 2r2 - R1
eq20 = X1^2 + r1^2 - (r1 + R1)^2
res11 = solve(eq20, R1)
res11[1] |> println
r0/15
R1 = r0/15
X1 = r0 - 2r2 - R1
(R1, X1)
(r0/15, 4*r0/15)
@syms R2, X2, Y2
(x1, y1, x2, y2) = (0, r1, r0 - r2, 0)
(R1, X1) = (r0/15, 4*r0/15)
eq21 = X2^2 + (Y2 - y1)^2 - (R2 + r1)^2
eq22 = (X2 - x2)^2 + (Y2 - y2)^2 - (R2 + r2)^2
eq23 = (X2 - x3)^2 + (Y2 - y3)^2 - (R2 + r3)^2
res12 = solve([eq21, eq22, eq23], (R2, X2, Y2))
2-element Vector{Tuple{Sym, Sym, Sym}}:
(-r0, 0, 0)
(r0/23, 12*r0/23, 8*r0/23)
@syms R3, X3, Y3
(R2, X2, Y2) = res12[2]
eq24 = X3^2 + (Y3 - y1)^2 - (R3 + r1)^2
eq25 = (X3 - x3)^2 + (Y3 - y3)^2 - (R3 + r3)^2
eq26 = (X3 - x4)^2 + (Y3 - y4)^2 - (R3 + r4)^2
res13 = solve([eq24, eq25, eq26], (R3, X3, Y3))
2-element Vector{Tuple{Sym, Sym, Sym}}:
(-r0, 0, 0)
(r0/39, 20*r0/39, 8*r0/13)
@syms R4, X4, Y4
#(x1, y1, x2, y2) = (0, r1, r0 - r2, 0)
(R3, X3, Y3) = res13[2]
eq27 = X4^2 + (Y4 - y1)^2 - (R4 + r1)^2
eq28 = (X4 - x4)^2 + (Y4 - y4)^2 - (R4 + r4)^2
eq29 = (X4 - x5)^2 + (Y4 - y5)^2 - (R4 + r5)^2
res14 = solve([eq27, eq28, eq29], (R4, X4, Y4))
2-element Vector{Tuple{Sym, Sym, Sym}}:
(-r0, 0, 0)
(r0/63, 4*r0/9, 16*r0/21)
@syms R5, X5, Y5
#(x1, y1, x2, y2) = (0, r1, r0 - r2, 0)
(R4, X4, Y4) = res14[2]
eq30 = X5^2 + (Y5 - y1)^2 - (R5 + r1)^2
eq31 = (X5 - x5)^2 + (Y5 - y5)^2 - (R5 + r5)^2
eq32 = (X5 - x6)^2 + (Y5 - y6)^2 - (R5 + r6)^2
res14 = solve([eq30, eq31, eq32], (R5, X5, Y5))
2-element Vector{Tuple{Sym, Sym, Sym}}:
(-r0, 0, 0)
(r0/95, 36*r0/95, 16*r0/19)
挟円のパラメータは
初円は
R1 = r0/15, X1 = 4*r0/15, Y1 = 0
二円以降 i ≧ 2 においては
半径 Ri = r0/(4i^2 - 4i + 15)
x座標 Xi = Ri * (8i - 4)
y座標 Yi = Ri * (4i^2 - 4i)
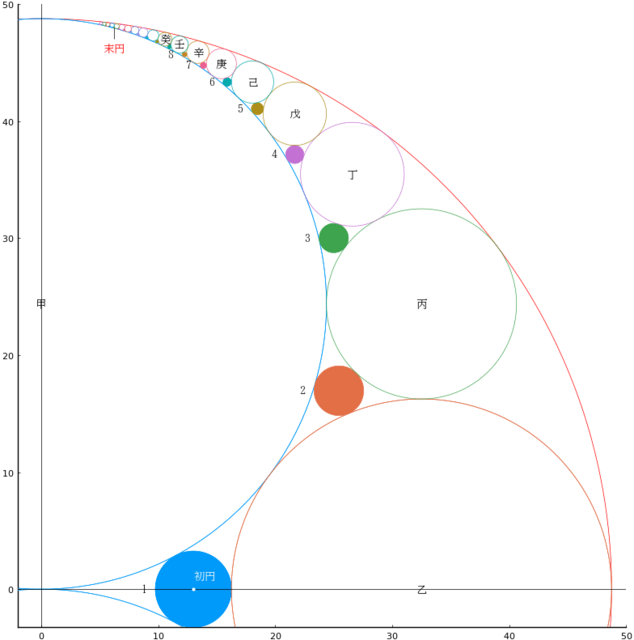
問は,「末円の径が一分であるとき,それは何番目の挟円か」ということである。
以下の方程式を解けば,16番目の挟円であることがわかる。
@syms i::positive
r0 = 975/20 # 直径 = 97.5
eq = r0/(4i^2 - 4i + 15) - 1//20 # 直径 = 0.1 寸
solve(eq, i)[1] |> println
16.0000000000000
一般的な解を求めるには,末円の半径を Rn とすれば
@syms i::positive, r0::positive, Rn::positive
eq = r0/(4i^2 - 4i + 15) - Rn
res = solve(eq, i)[2]
res |> println
1/2 + sqrt(-14*Rn + r0)/(2*sqrt(Rn))
SymPy ではこれ以上簡単にできないが,手計算で,(1 + sqrt(r0/Rn - 14))/2 となる。
「外円の半径を末円の半径で割り,14を引いて,開平し,1を加えて,2で割る」となり,「術」と一致する。
なお,当たり前であるが,術は,半径を直径と読み替えても成り立つ。
ちなみに,20番目の挟円の半径は 0.031759 ほどであり,数値を丸めるとたしかに20番目である事がわかる。
(sqrt(97.5/(2*0.031759) - 14) + 1)/2
19.99998688035496
それぞれの円のパラメータは以下通り。
番号: 累円 xi, 累円 yi, 累円 ri; 挟円 Xi, 挟円 Yi, 挟円Ri
1: 0.000000, 24.375000, 24.375000; 13.000000, 0.000000, 3.250000
2: 32.500000, 0.000000, 16.250000; 25.434783, 16.956522, 2.119565
3: 32.500000, 24.375000, 8.125000; 25.000000, 30.000000, 1.250000
4: 26.590909, 35.454545, 4.431818; 21.666667, 37.142857, 0.773810
5: 21.666667, 40.625000, 2.708333; 18.473684, 41.052632, 0.513158
6: 18.055556, 43.333333, 1.805556; 15.888889, 43.333333, 0.361111
7: 15.394737, 44.901316, 1.282895; 13.852459, 44.754098, 0.266393
8: 13.382353, 45.882353, 0.955882; 12.238494, 45.690377, 0.203975
9: 11.818182, 46.534091, 0.738636; 10.940594, 46.336634, 0.160891
10: 10.572289, 46.987952, 0.587349; 9.880000, 46.800000, 0.130000
11: 9.558824, 47.316176, 0.477941; 9.000000, 47.142857, 0.107143
12: 8.719512, 47.560976, 0.396341; 8.259669, 47.403315, 0.089779
13: 8.013699, 47.748288, 0.333904; 7.629108, 47.605634, 0.076291
14: 7.412281, 47.894737, 0.285088; 7.086137, 47.765814, 0.065612
15: 6.893939, 48.011364, 0.246212; 6.614035, 47.894737, 0.057018
16: 6.442731, 48.105727, 0.214758; 6.200000, 48.000000, 0.050000
17: 6.046512, 48.183140, 0.188953; 5.834089, 48.087035, 0.044198
18: 5.695876, 48.247423, 0.167526; 5.508475, 48.159806, 0.039346
19: 5.383436, 48.301380, 0.149540; 5.216920, 48.221258, 0.035249
20: 5.103306, 48.347107, 0.134298; 4.954397, 48.273616, 0.031759
function circle4f(x, y, r, color=:red)
circlef(x, y, r, color)
circlef(x, -y, r, color)
circlef(-x, y, r, color)
circlef(-x, -y, r, color)
end;
function draw(more=false)
pyplot(size=(800, 800), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
n = 20
names = Char["甲乙丙丁戊己庚辛壬癸"...]
r = Vector{Float64}(undef, n)
x = Vector{Float64}(undef, n)
y = Vector{Float64}(undef, n)
r0 = 975//20
r1 = r0/2
r2 = r0/3
x2 = r0 - r2
(r[1], x[1], y[1]) = (r1, 0, r1)
(r[2], x[2], y[2]) = (r2, x2, 0)
for i in 3:n
factor = r0/(i^2 - 2i + 3)
r[i] = factor
x[i] = factor*(2i - 2)
y[i] = factor*(i^2 - 2i)
end
R = Vector{Float64}(undef, n)
X = Vector{Float64}(undef, n)
Y = Vector{Float64}(undef, n)
(R[1], X[1], Y[1]) = (r0/15, 4*r0/15, 0)
for i in 2:n
factor = r0/(4i^2 - 4i + 15)
R[i] = factor
X[i] = factor*(8i - 4)
Y[i] = factor*(4i^2 - 4i)
end
plot()
circle(0, 0, r0)
@printf("%4s: %9s, %9s, %9s; %9s, %9s, %9s\n", "番号", "累円 xi", "累円 yi", "累円 ri", "挟円 Xi", "挟円 Yi", "挟円Ri")
for i in 1:n
@printf("%4i: %9.6f, %9.6f, %9.6f; %9.6f, %9.6f, %9.6f\n", i, x[i], y[i], r[i], X[i], Y[i], R[i])
circle4(x[i], y[i], r[i], i)
circle4f(X[i], Y[i], R[i], i)
i < 11 && point(x[i], y[i], names[i], :black, :center, :vcenter, mark=false)
i < 9 && point(X[i]-R[i]-1, Y[i], string(i), :black, :center, :vcenter, mark=false)
end
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
point(X[1], Y[1], "初円", :white, :left, :bottom, delta=delta/2)
segment(X[16], Y[16], X[16], Y[16] - 1)
point(X[16], Y[16] - 1, "末円", :red, :center, :top, delta=-delta/4, mark=false)
plot!(xlims=(-2, 50), ylims=(-R[1], 50))
end
end;