対戦ゲームのチームはどう決める?
締め切りが 2017/11/30 10:00 AM なので,その 1 分後に投稿されるように予約
設問
あなたは対戦型オンラインゲームの開発に携わっており、チームバトルにおける「マッチング」のアルゴリズム開発を任されました。
なお、マッチングとは、同一時間に同一のゲームができるようプレイヤー同士を引き合わせことで、どちらかのチームが極端に有利にならないよう、メンバーを決める必要があります。
求められるプログラムの前提条件は、以下の通りとなります。
・ 標準入力から、以下の書式の文がプレイヤーの人数分、複数行送られる
プレイヤーのID プレイヤーのレート
・ プレイヤーのIDは、0から始まる連番の数値である
・ プレイヤーのレートは、1桁以上4桁以下の正の整数とする
・ チームバトルの候補となるプレイヤーは、4人以上20人以下とする
・ チームバトルは2人対2人の2チームによる対戦とし、メンバーの欠員は認めないものとする
・ チームに所属するメンバー全員のレートを合計したものをチームレートと呼ぶ
・ チームメンバーは、チームレートの差の絶対値が最小となるように決めること
・ チームメンバーの最適解が複数存在するケースは考慮しなくともよい。
※ 簡単のため、最適解は1つとなるように入力データが調整される
・ 選んだチームメンバーの中で、最もIDが小さいプレイヤーが所属するチームをチームAと呼び、もう一方をチームBとする
・ 標準出力に、チームAのメンバー全員のIDをIDの値が昇順となるよう、スペース区切りで出力し、次に改行した上で、同様にチームBのメンバー全員のIDを昇順で出力する
そして 以下が、入力と出力例になります。
上記の例でNo.1の場合、チームレートは 2389+1894と1363+2865 となり、その差の絶対値は 55 となります。
そしてNo. 2は、No.1 に1プレイヤーを加えたものですが、差の絶対値は 2 となります。
マッチングというのも実に奥が深いテーマで、上記のような実力差だけで選んでしまうと、実力が平均に近いプレイヤーが集中的に選ばれてしまいます。
そこで、快適に遊んでもらうために、プレイヤーの待ち時間といったものを考慮する必要があるでしょう。
また、人数が増えた場合にどう高速化するかという課題も出てきます。
もしかすると普段貴方が遊んでいるゲームの裏側では、実に大変な組合せ最適化問題をバックエンドで解いているかもしれませんね。
それでは、ぜひ挑戦してみてください!
【問題】
標準入力から、プレイヤーのIDとレート(腕前を数値化したもの)が、プレイヤーの人数分複数行送られます。
ここで、2人対2人のチームバトルを想定したとき、チーム間の実力がなるべく均衡するように、チームメンバーを決め、その結果を標準出力に返してください。
==============================
f = function(x) {
n = length(x)/2
rate = x[1:n*2]
teamRate = outer(rate, rate, "+")
minDif = Inf
a = combn(n, 2) # n 人から 2 人取り出す組み合わせ
for (i in 1:ncol(a)) {
a1 = a[1, i]
a2 = a[2, i]
teamRateA = teamRate[a1, a2]
b = combn((1:n)[-a[, i]], 2) # a チーム以外の n-2 人から 2 人取り出す組み合わせ
for (j in 1:ncol(b)) {
b1 = b[1, j]
b2 = b[2, j]
teamRateB = teamRate[b1, b2]
dif = abs(teamRateA-teamRateB)
if (dif < minDif) {
minDif = dif
ID = c(a1, a2, b1, b2)-1
}
}
}
cat(sprintf("%i %i\n", ID[1], ID[2]), sprintf("%i %i\n", ID[3], ID[4]), sep="")
}
# f(scan(file("stdin", "r")))
f(c(0, 1000, 1, 2122, 2, 2389, 3, 1363, 4, 1894, 5, 2865)) # (2, 4), (3, 5)
f(c(0, 1000, 1, 2122, 2, 2389, 3, 1363, 4, 1894, 5, 2865, 6, 1761)) # (0, 1), (3, 6)
f(c(0, 1987, 1, 1521, 2, 987, 3, 1201, 4, 1055, 5, 1763, 6, 2469, 7, 2017)) # (0, 2), (3, 5)
f(c(0, 1987, 1, 1521, 2, 987, 3, 1201, 4, 1055, 5, 1763, 6, 2469, 7, 2017,
8, 2890, 9, 2345, 10, 1609, 11, 3101)) # (2, 11), (3, 8)
f(c(0, 1987, 1, 1521, 2, 987, 3, 1201, 4, 1055, 5, 1763, 6, 2469, 7, 2017,
8, 2890, 9, 2345, 10, 1609, 11, 3101,
12, 3689, 13, 876, 14, 3309, 15, 785, 16, 2678, 17, 3586, 18, 3321, 19, 2643)) # (1, 10), (9, 15)
単調増加連数
締め切りが 2017/11/24 10:00 AM なので,その 1 分後に投稿されるように予約
【概要】
正の整数を 2進数で表現したときに、1や0の続く長さがどんどん増えていく数を「単調増加連数」と呼びます。例えば以下のとおりです:
値(10進数表示) 値(2進数表示) 1や0の続く長さ 単調増加連数?
7 111 3 TRUE
10 1010 1, 1, 1, 1 FALSE
77 1001101 1, 2, 2, 1, 1 FALSE
79 1001111 1, 2, 4 TRUE
240 11110000 4, 4 FALSE
399 110001111 2, 3, 4 TRUE
1136 10001110000 1, 3, 3, 4 FALSE
3975 111110000111 5, 4, 3 FALSE
293888 1000111110000000000 1, 3, 5, 10 TRUE
入力された値よりも大きな「単調増加連数」で、最も小さいものを出力してください。
【入出力】
入力は77のようになっています。普通に 10進数です。
出力も普通に10進数です。77 より大きな「単調増加連数」として最も小さい値を出力すれば良いので、77に対応する出力は79です。
【例】
入力 入力の2進数表示 出力 出力の2進数表示 出力の1や0の続く長さ
77 1001101 79 1001111 1, 2, 4
79 1001111 96 1100000 2, 5
57 111001 63 111111 6
【補足】
• 不正な入力に対処する必要はありません。
• 入力は 1 以上 百億以下です。
• 「単調増加連数」は、この問題のために作った造語です。
================================================================================
n を 1 ずつ増やして...なんて,普通にやったら n が大きいときには日が暮れる。
紙に書いてやれば,簡単に答えが得られる。しかし,アルゴリズムをプログラム化するのが面倒。
n より大きい数で,その二進表記のビット列が「1 が a1 個, 0 が a2 個, また 1 が a3 個, 0 が a4 個 …」のようになっていて,a1 < a2 < a3 < a4 < … < ak である二進数の最小値を求めるということ。
n+1 のビット列の長さが 8 の場合だと,8 を要素数の相異なる部分に分割する方法は,(8), (7,1), (6,2), (5, 3), (5, 2, 1), (4, 3, 1) の 6 通り。
それぞれは
11111111
11111110
11111100
11111000
11111001
11110001
これを十進数に変換して,n より大きくて最小のものを求めればよい。
initDiv = function(length, max) {
ary = NULL
repeat {
if (max >= max) {
ary = c(ary, length)
return(ary)
} else {
ary = c(ary, max)
length = length - max
}
}
}
nextDiv = function(ary) {
repeat { # 1でない要素を後ろから探す
sum = 0
for (pos in length(ary):1) {
a = ary[pos]
sum = sum + a
if (a != 1) {
break
}
}
if (ary[1] == 1) { # 全て1
return(FALSE)
}
ary = ary[1:pos]
ary[pos] = ary[pos] - 1
max = ary[pos]
sum = sum - max
pos = pos + 1
repeat {
if (max >= sum) {
ary[pos] = sum
return(ary)
} else {
ary[pos] = max
sum = sum - max
}
pos = pos + 1
}
}
}
f = function(n) {
minAns = Inf # n+1 以上で,条件を満たす最小の整数
length = max = floor(log2(n+1))+1 # n+1 を二進表記したときの桁数
weight = 2^((length - 1):0)
first = TRUE
repeat { # 整数分割
if (first) {
d = initDiv(length, max)
first = FALSE
} else {
d = nextDiv(d)
if (length(d) == 1) {
break
}
}
if (length(unique(d)) == length(d)) { # ある分割の要素数が全部違うものが探索対象
D = rev(d) # 例えば,ビット列の長さが 8 なら,d は (8), (7,1), (6,2), (5, 3), (5, 2, 1), (4, 3, 1)
bit = NULL # それぞれの D (d の逆順)の奇数番目は 1 の繰り返し数,偶数番目は 0 の繰り返し数
for (i in seq_along(D)) { # d = (5, 2, 1), D = (1,2,5) なら bit = (1, 0, 0, 1, 1, 1, 1, 1)
bit = c(bit, rep(i%%2, D[i]))
}
ans = sum(bit * weight) # 二進数の bit 列を十進数に変換
if (minAns > ans && ans > n) { # その数が n より大きくて最小のものが解 minAns
minAns = ans
}
}
}
cat(minAns)
}
# f(scan(file("stdin", "r")))
f(77) # 79
f(79) # 96
f(57) # 63
f(1) # 3
f(3) # 4
f(1e+10) # 10468982784
f(1228) # 1248
f(160199) # 161792
f(5368709119) # 6442450944
f(29614080) # 29614207
f(575) # 624
f(19968) # 19999
f(1278987) # 1279936
f(163831842) # 163831935
f(587776) # 588800
「ストレート・ラインズ」問題
締め切りが 2017/11/23 10:00 AM なので,その 1 分後に投稿されるように予約
設問
2 以上の自然数 n に対し、n×n の格子状に並んだ点を考えます。
これらの点のうちちょうど 2 個の点を通る直線の数を F(n) と定義します。
例えば F(2)=6 です。題意を満たす直線は以下の 6 通りです。
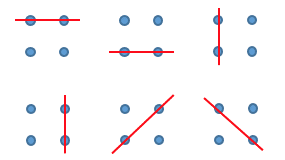
また、F(3)=12 です。題意を満たす直線は以下の 12 通りです。

同様に、F(4)=48, F(5)=108, F(6)=248, F(7)=428, F(10)=1900 となることが確かめられます。
標準入力から、自然数 n (2 ≦ n ≦ 40)が与えられます。
標準出力に F(n) の値を出力するプログラムを書いてください。
===================================
問題文中にある数列情報だけで,オンライン整数列大辞典の A018809 であることがわかる。その説明書きが "Number of lines through exactly 2 points of an n X n grid of points." と,問題の趣旨そのものである。
ただ,記事中の (x, y) = 1 というのが何なのか,分からなかったが,関連する論文を読んで,「x, y の最大公約数が 1」ということが分かったのでプログラムを書き下ろす。
euclid = function(m, n) {
repeat {
temp = n%%m
if (temp == 0) {
return(m)
}
n = m
m = temp
}
}
g = function(n, k) {
count = 0
for (x in 0:n) {
for (y in 0:n) {
if (x != 0 && y != 0 && euclid(x, y) == k)
count = count + (n - x) * (n - y)
}
}
count
}
f = function(n) {
if (n == 2) {
cat(6)
} else {
cat(2 * g(n, 3) - 4 * g(n, 2) + 2 * g(n, 1))
}
}
# f(scan(file("stdin", "r")))
# n: 0 1 2 3 4 5 6 7 8 9 10
# f(n): 0, 0, 6, 12, 48, 108, 248, 428, 764, 1196, 1900
f(13) # 5244
f(27) # 98492
f(38) # 388212
f(40) # 475068
コメントをいただいた
> pythonは標準ではRで言うlistで配列を扱うので, 標準では速度的に不利です。それをRと同じようにベクトル(配列)で扱えるようにするのがnumpyですので,
> numpy.mean(numpy.arange(1,10000000))
> みたいにして比較するなら良いかと思います。
> 上記のpythonの例だと, Rで言うなれば x にたような比較になってしまっています。
> # つまりリスト処理のオーバーヘッドの計測をしてしまっている.
なるほど,遅すぎるとは思いました。
しかし,以下のようにしてみましたが,
>>> import numpy
>>> import time
>>> s = time.time()
>>> numpy.mean(numpy.arange(1,10000001))
5000000.5
>>> print(time.time()-s)
0.1522839069366455
しかしなおかつ,10倍ほど遅い(まあ,1秒以下なんだから,大人げなく目くじら立てるほどでもないが)
なお,重箱の隅突きで申し訳ないが,
numpy.arange(1,10000000)
ではなくて,
numpy.arange(1,10000001)
これも,python のやーーなところ(^_^)
=====
R でリストを使うと遅いだろうという指摘はごもっとも
> options(digits=16)
> system.time({
+ x = as.list(1:10000000)
+ Sum = 0
+ for (i in x) Sum = Sum+x[[i]]
+ print(Sum/length(x))
+ })
[1] 5000000.5
ユーザ システム 経過
0.68999999999999773 0.01800000000000068 0.70499999999992724
でも,list は使わないし...大部分は for のせいだし...
========
追加,上述 python3 の実行結果は,当然ながら,コンソールで逐一入力したものではない(そりゃそうでしょ)
しかし,一行ずつのスクリプトを入力するのではなく,以下のように,全行まとめてやるとずっと速いということがわかった
>>> s=time.time();np.mean(np.arange(1,10000001));print(time.time()-s)
5000000.5
0.03643488883972168
パーサー(?)に一括して渡すかどうかの違いかな?
ごく普通の数学問題を解くプログラムを R と Python3 で書いた場合,後者は前者の数倍遅い
プログラムの可読性では,Python3 の「ブロック:インデントルール」で大変,読みにくい
オブジエクト・オリエンティッドと関数の関係に一致性がなく,理解困難
ということで,Python を使う意味を見いだせない
崩れないように積み上げて!
締め切りが 2017/11/21 10:00 AM なので,その 1 分後に投稿されるように予約
直方体の箱を重ねて置くことを考えます。
ただし、上の箱は下の箱よりも小さくないと、崩れてしまう可能性があります。
そこで、大きな箱の上に小さな箱を置くことを考えます。
ここで「小さい」とは縦と横の長さがともに短いことにします。
つまり、中央に重ねて置くと、上から見たときに下の箱の輪郭が見えるようにします。
また、箱は縦か横方向に綺麗に置くものとし、斜めに傾けて置くことはありません。
m 個の箱を用意したとき、その上面の面積の和が n でした。
このような箱のサイズの組み合わせが何通りあるか求めてください。
ただし、辺の長さはいずれも正の整数とし、箱の高さは考えないものとします。
なお、同じサイズの箱でも縦と横の置き方が違う場合は別々にカウントします。
例えば、m = 3, n = 20 のとき、上から見ると以下の4通りがあります。
同様に、m = 2, n = 14 のとき、上から見ると以下の8通りがあります。
標準入力から m, n が与えられたとき、その箱のサイズの組み合わせを求め、その数を標準出力に出力してください。
なお、m, n は 0 < m < n < 250を満たす整数とします。
【入出力サンプル】
標準入力
3 20
標準出力
4
======================================================================
所詮 R では m < 5 程度まで
Div = function(m, n) {
d = NULL
if (m == 2) {
for (i1 in n:1) {
for (i2 in i1:1) {
if (i1 + i2 == n) {
d = rbind(d, c(i1, i2))
}
}
}
} else if (m == 3) {
for (i1 in n:1) {
for (i2 in i1:1) {
i12 = i1 + i2
if (i1 + i2 >= n)
next
for (i3 in i2:1) {
if (i1 + i2 + i3 == n) {
d = rbind(d, c(i1, i2, i3))
}
}
}
}
} else if (m == 4) {
for (i1 in n:1) {
for (i2 in i1:1) {
i12 = i1 + i2
if (i12 >= n)
next
for (i3 in i2:1) {
i123 = i12 + i3
if (i123 >= n)
next
for (i4 in i3:1) {
if (i1 + i2 + i3 + i4 == n) {
d = rbind(d, c(i1, i2, i3, i4))
}
}
}
}
}
}
return(d)
}
f = function(m, n) {
D = Div(m, n)
count = 0
for (k in 1:nrow(D)) {
d = D[k, ]
a = vector("list", m)
for (i in 1:m) {
x = 1:floor(sqrt(d[i]))
temp = x[(d[i]%/%x) == (d[i]/x)]
temp = sort(unique(c(temp, d[i]/temp)))
a[[i]] = temp
}
if (m == 2) {
for (i1 in 1:length(a[[1]])) {
a1 = a[[1]][i1]
b1 = d[1]/a1
for (i2 in 1:length(a[[2]])) {
a2 = a[[2]][i2]
b2 = d[2]/a2
if (a1 > a2 && b1 > b2) {
count = count + 1
}
}
}
} else if (m == 3) {
for (i1 in 1:length(a[[1]])) {
a1 = a[[1]][i1]
b1 = d[1]/a1
for (i2 in 1:length(a[[2]])) {
a2 = a[[2]][i2]
b2 = d[2]/a2
for (i3 in 1:length(a[[3]])) {
a3 = a[[3]][i3]
b3 = d[3]/a3
if (a1 > a2 && a2 > a3 && b1 > b2 && b2 > b3) {
count = count + 1
}
}
}
}
} else if (m == 4) {
for (i1 in 1:length(a[[1]])) {
a1 = a[[1]][i1]
b1 = d[1]/a1
for (i2 in 1:length(a[[2]])) {
a2 = a[[2]][i2]
if (a2 >= a1)
next
b2 = d[2]/a2
if (b2 >= b1)
next
for (i3 in 1:length(a[[3]])) {
a3 = a[[3]][i3]
if (a3 >= a2)
next
b3 = d[3]/a3
if (b3 >= b2)
next
for (i4 in 1:length(a[[4]])) {
a4 = a[[4]][i4]
if (a4 >= a3)
next
b4 = d[4]/a4
if (b4 >= b3)
next
count = count + 1
}
}
}
}
}
}
cat(count)
}
system.time(f(2, 14)) # 8
system.time(f(3, 20)) # 4
system.time(f(4, 100)) # 466 # 1.694 sec.
n ごとに最適化して Java プログラムを書くことで,どうにか実行時間を 1 秒以内に収まる
1 から 10000000 までの整数の平均値
Python3
>>> import time; import statistics; start=time.time();statistics.mean(list(range(1,10000001)));print(time.time()-start)
5000000.5
9.593008995056152 # 9 秒もかかる?
>>> import time; import numpy; start=time.time();numpy.mean(list(range(1,10000001)));print(time.time()-start)
5000000.5
1.1983740329742432 # numpy でも 1 秒
R
> optons(digits=16)
> system.time(print(mean(1:10000000)))
[1] 5000000.5
ユーザ システム 経過
0.016000000000005343 0.008000000000002672 0.023999999999887223 # 0.02 秒以下なんだが
http://my-notes.hatenablog.com/entry/2017/11/19/022246
結果の表示が特殊
sympy がインストールされていない場合は,事前に一度だけ
$ python3 -m pip install sympy
その後,
$ python3
>>> import sympy as sym
>>> sym.factorint(12878)
{2: 1, 47: 1, 137: 1}
>>> sym.factorint(111111111111111111111111111111111111111111111111111111111111111)
{3: 2, 37: 1, 43: 1, 239: 1, 1933: 1, 4649: 1, 10837: 1, 23311: 1, 45613: 1, 333667: 1, 45121231: 1, 10838689: 1, 1921436048294281: 1}
>>> start=time.time();sym.factorint(11111111111111111111111111111111111111111111111111111111111111111111);print(time.time()-start)
{11: 1, 101: 1, 103: 1, 4013: 1, 2071723: 1, 28559389: 1, 1491383821: 1, 5363222357: 1, 21993833369: 1, 2324557465671829: 1}
1.9484901428222656 # 1.9 秒かかりました
R で素因数分解
gmp がインストールされていない場合は,事前に一度だけ
> install.packages("gmp")
gmp を使う前に
> library(gmp)
その後,
> factorize(12878)
Big Integer ('bigz') object of length 3:
[1] 2 47 137
> factorize(as.bigz("111111111111111111111111111111111111111111111111111111111111111"))
Big Integer ('bigz') object of length 14:
[1] 3 3 37 43 239 1933 4649
[8] 10837 23311 45613 333667 45121231 10838689 1921436048294281
> system.time(print(factorize(as.bigz("11111111111111111111111111111111111111111111111111111111111111111111"))))
Big Integer ('bigz') object of length 10:
[1] 11 101 103 4013 2071723 28559389 1491383821
[8] 5363222357 21993833369 2324557465671829
ユーザ システム 経過
0.03 0.00 0.03 # 0.03秒でした
マス目を回す
締め切りが 2017/11/17 10:00 AM なので,その 1 分後に投稿されるように予約
【概要】
4×4 のマス目があります。
マス目のうちいくつかは穴になっています。
abc-/d-ef/g-hi/opqr codeiqのような形で盤面の初期状態(abc-/d-ef/g-hi/opqr)と一連の操作(codeiq)を与えます。
操作は一連の文字です。
各文字は「その文字を中心として、隣接(斜め含む)しているマスの文字を時計回りに回す」という操作を示しています。
ただし、穴の位置は変えないようにします。
一連の操作を終えたあとのマス目の状態を出力して下さい。
【入出力】
入力は
abc-/d-ef/g-hi/opqr codeiq
のようになっています。
空白の前が4×4のマス目、空白の後が一連の操作です。
マス目はスラッシュ区切りで各行を表しています。
a~z は普通のマス、「-」は穴を意味します。
c を中心として回した後は,以下のようになります。

出力は、最終的なマス目の状態です。
形式は入力の空白の前の文字列と同じです。
abc-/d-ef/g-hi/opqr codeiqに対応する出力は
pac-/o-dh/e-qf/grbi
です。
【例】
入力 出力
abc-/d-ef/g-hi/opqr codeiq pac-/o-dh/e-qf/grbi
na-c/d-be/t---/g-hi nabetani ab-t/c-en/d---/g-hi
ab--/----/----/---c abcabc ab--/----/----/---c
【補足】
• 不正な入力に対処する必要はありません。
• 異なるマス目に同じアルファベットが割り当てられることはありません。
• 操作を表すアルファベットは、1文字以上10文字以下です。
• マス目に含まれない文字が、操作を表す文字に含まれることはありません。
----------------------------------------------------------------------------------------------------
f = function(s) {
s = unlist(strsplit(s, " "))
s1 = matrix("-", 6, 6)
s1[2:5, 2:5] = t(matrix(unlist(strsplit(gsub("/", "", s[1]), "")), 4, 4))
s2 = unlist(strsplit(s[2], ""))
modify.i = c(-1, -1, -1, 0, 1, 1, 1, 0)
modify.j = c(-1, 0, 1, 1, 1, 0, -1, -1)
for (char in s2) {
suf = which(s1 == char, arr.ind=TRUE)
suf.i = suf[1]
suf.j = suf[2]
i = j = integer(8)
cell = 0
for (k in 1:8) {
if (s1[suf.i+modify.i[k], suf.j+modify.j[k]] != "-") {
cell = cell+1
i[cell] = suf.i+modify.i[k]
j[cell] = suf.j+modify.j[k]
}
}
if (cell > 1) {
temp = s1[i[cell], j[cell]]
for (k in cell:2) {
s1[i[k], j[k]] = s1[i[k-1], j[k-1]]
}
s1[i[1], j[1]] = temp
}
}
result = character(4)
for (i in 2:5) {
result[i-1] = paste(s1[i, 2:5], collapse="")
}
cat(result, sep="/")
}
#f(readLines(file("stdin", "r")))
f("abc-/d-ef/g-hi/opqr codeiq") # pac-/o-dh/e-qf/grbi
f("---y/-x--/----/---z xyz") # ---y/-x--/----/---z
f("al-d/yteq/ukwg/-pmc yptawa") # ka-d/luye/cmpq/-wtg
f("y---/-o-e/v--b/---a eaeyyvva") # y---/-o-e/v--b/---a
f("s-jq/----/p---/-cy- yccpyycs") # s-jq/----/y---/-cp-
f("epns/cvbz/igrd/mqyo ydcmzvs") # iebn/cpqy/mogs/rvdz
f("kiy-/-ogn/ebua/vq-l euvoei") # bqo-/-vik/engy/lu-a
f("-ply/-wb-/zg-s/m-e- zpgeyelz") # -blp/-wm-/gz-s/e-y-
f("e-sr/l---/----/---k lslek") # e-sr/l---/----/---k
f("---q/-wr-/---a/---- qrqwawqrww") # ---a/-qr-/---w/----
f("fhkr/-qip/zldy/cgvu pcgvrpkciu") # gfdi/-cvh/lzyk/ruqp
f("klfs/r-cw/mdnb/tp-- ppsffmpw") # kbfm/r-tw/dncl/sp--
f("tm--/ukfh/oldy/jcxa dyxjcuo") # ht--/jolm/cfuk/xayd
PIAAC データ解析
https://oku.edu.mie-u.ac.jp/~okumura/stat/piaac.html
> まったく相関がないように見える。ただ,強引に相関係数を求めて検定してみると
:
> -0.02 という非常に小さな負の相関があり,非常に小さいにもかかわらずp値はほぼ0で非常に有意である。このあたりが大量のデータを扱う上での落とし穴である。
> この落とし穴をもうちょっと詳しく調べてみよう。例えば日本(392)だけに限って調べる。
:
> やはり目で見ても顕著ではないが,正の小さな相関 0.04 があり,p = 0.01 で有意である。
> では,知的好奇心が労働時間と国の両方に関係しているというモデルで調べてみよう。
:
> 労働時間が1時間増えるごとに知的好奇心は 0.001 増える。非常に有意(p = 5e-12)である。
こういうことを言うことが,統計学を貶めることになるのでは?
なんだろうね。ふしぎだ
> 結論:国レベルでは,労働時間が増えるほど知的好奇心は減る。個人レベルでは,労働時間が増えるほど知的好奇心は増える。
全く不適切なまとめでなないですか?
労働時間と知的好奇心は無関係
忙しくても(勉強の時間が少なくても)新しいことを学びたいと思う(実行している)人はいる
忙しくて勉強の時間もないから,残念ながら新しいことを学べないでいる人もいる
時間が十分あるから,新しいことを学んでいる人もいる
暇でも,のんべんだらりと暮らしている人もいる
それを知りたいなら,それを調べればよい。労働時間と知的好奇心を聞いても真実は分からない(隔靴掻痒)
既存の統計で,おざなりな解析をして,ご託を並べる(それをインターネットの記事に上げる)のはどうかなあ??
あー,私もそうですね〜〜
奥村先生が,「PIAACデータ解析」を書いている。(途中みたいだが)
https://oku.edu.mie-u.ac.jp/~okumura/stat/piaac.html
そのきっかけは
https://twitter.com/tmaita77/status/930020451899678720
https://twitter.com/kohske/status/930218156508946432
のようであるが,以下のようなプロットを作成すれば,実態が見えてくる。
データは31カ国の wh: 週あたり仕事時間(連続量) と ll: 新しいことを学ぶのが好き(5段階)
ただし,1カ国は wh が全て欠損値のため相関係数が計算できない(ので,除外する)
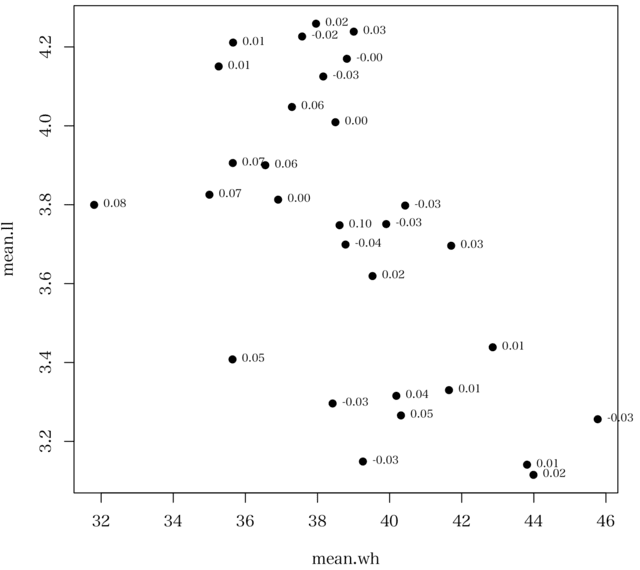
図には,黒丸で30カ国の wh, ll の平均値がプロットされている。
隣にある数値は,それぞれの国の対象者についての wh と ll のピアソンの積率相関係数である。各国での相関係数は小さなものである。無相関といってよい。
しかし,30カ国の wh と ll の平均値をデータとしたピアソンの積率相関係数はなんと -0.581 になる!!(図からも予想できるが)。なお,厳密にいえば(こんなところで厳密もへったくれもないが),30 個のデータ点はそれぞれの背景となったサンプルサイズによる重み付けが必要。
素データを国ごとにまとめた平均値間の相関係数は,実態を表さないのである。
もとの分析は,「新しいことを学ぶのが好き」の上位 2 カテゴリーに属するか否かの 2 値データにしたり,30〜40 歳代のフルタイムワーカーに限定したりしているが,大局的には大差ない。
また,「新しいことを学ぶのが好き」がカテゴリーデータなので,順位相関係数を求めても,またプロットの縦軸を mediann にしても,これまた大局的に大差ない。
library(data.table)
data = fread("all.dat")
cntryid = factor(data$CNTRYID)
wh = as.numeric(data$D_Q10) # 週あたり仕事時間
ll = as.numeric(data$I_Q04d) # 新しいことを学ぶのが好き
cor.wh.ll = sapply(data3, function(d) {
d2 = subset(d, complete.cases(d))
if (nrow(d2) == 0) NA else cor(d2$wh, d2$ll, use="complete.obs")
})
mean.wh = sapply(data3, function(d) mean(d$wh, na.rm=TRUE))
mean.ll = sapply(data3, function(d) mean(d$ll, na.rm=TRUE))
cor(mean.wh, mean.ll, method="spearman", use="complete.obs")
plot(mean.wh, mean.ll, pch=19)
text(mean.wh, mean.ll, sprintf("%.2f", cor.wh.ll), cex=0.7, pos=4, xpd=TRUE)
なお,all.dat は gawk, getdata.awk を使って
$ gawk -f getdata.awk *.csv > all.dat
で作成する(なんとなれば,それぞれの .csv ファイルの1行目が変数名なので)
getdata.awk ファイルの内容
NR == 1 { print }
FNR != 1 {print}
カウントゲームで先手が勝つのは何通り?
締め切りが 2017/11/14 10:00 AM なので,その 1 分後に投稿されるように予約
某SNSにおいて、チャットでAIと対戦できる「カウントゲーム」があります。
ある数からスタートし、交互に最大3つまでの数をカウントダウンしていき、最後に「0」を言った方が負け、というゲームです。
例えば、AとBが対戦し、Aが15からスタートして、以下のように進むとBの負けとなります。
A「15, 14」
B「13, 12」
A「11, 10, 9」
B「8」
A「7」
B「6, 5, 4」
A「3, 2, 1」
B「0」
なお、自分から負けるために、「1, 0」のように言うことはないものとします。
(相手が「1」まで言って、最後に「0」だけを言って負ける)
標準入力から整数 n が与えられたとき、Aが n からスタートし、最後にBが「0」を言うパターンが何通りあるか求め、標準出力に出力してください。
なお、n は1≦n≦50を満たすものとします。
例えば、n = 5のとき、以下の7通りがあります。
【入出力サンプル】
標準入力
5
標準出力
7
==============================
整数分割法+同じものが複数あるときの並べ替えの個数の問題
initDiv = function(length, max) {
ary = NULL
repeat {
if (length <= max) {
ary = c(ary, length)
return(ary)
} else {
ary = c(ary, max)
length = length - max
}
}
}
nextDiv = function(ary) {
repeat { # 1でない要素を後ろから探す
sum = 0
for (pos in length(ary):1) {
a = ary[pos]
sum = sum + a
if (a != 1) {
break
}
}
if (ary[1] == 1) { # 全て1
return(FALSE)
}
ary = ary[1:pos]
ary[pos] = ary[pos] - 1
max = ary[pos]
sum = sum - max
pos = pos + 1
repeat {
if (sum <= max) {
ary[pos] = sum
return(ary)
} else {
ary[pos] = max
sum = sum - max
}
pos = pos + 1
}
}
}
check = function(d) {
n = length(d)
if (n %% 2 == 0) { # 先手が勝つためには奇数回
return(0)
} else { # 同じものが複数あるときの並べ替えの個数
res = factorial(n)
for (i in table(d)) {
res = res/factorial(i)
}
return(res)
}
}
f = function(length) {
count = 0
d = initDiv(length, 3)
count = count+check(d)
repeat {
d = nextDiv(d)
count = count+check(d)
if (d[1] == 1) { # 毎回 1 ずつというのが最終
break
}
}
options(scipen=100)
cat(count)
}
# f(scan(file("stdin", "r")))
f(5) # 7
f(6) # 12
f(15) # 2884
f(25) # 1277879
f(50) # 5281115313321
js-STAR version 8.9.6j(β版)
ちゃんとプログラム実行結果の検証をしているのか?
みっともないぞ
[直接確率計算2×2]で,どうやったら,「両側検定 : p=0.0000 ns (.10<p)」なんて結果になるんだ?
「カイ二乗検定の結果」で,4つのセルが全く同じ場合(例えば,10,10,10,10)でもカイ二乗値が0ではない( 0.1 になる)とは,なんたる惨状!
[直接確率計算2×2]
観測値1 観測値2
-----------------------------------------
群1 10 9
群2 7 8
-----------------------------------------
両側検定 : p=0.0000 ns (.10<p)
以下略
=============================
「カイ二乗検定の結果」
(上段実測値,下段期待値)
----------------
10 10
10.000 10.000
----------------
10 10
10.000 10.000
x2(1)= 0.100 , ns
=============================
他にも p 値の表示エラーはいくつかのプログラムにある。
[直接確率計算2×2] で
40 2
5 30
の検定結果が 「両側検定 : p=6.0000 ** (p<.01)」と表示される
どうもこれは,
> fisher.test(matrix(c(40, 5, 2, 30), 2))
Fisher's Exact Test for Count Data
data: matrix(c(40, 5, 2, 30), 2)
p-value = 6.108e-14
の,指数表示されたときの p 値の最上位桁の 6 を拾っているようだ。
40 2
5 31
の検定結果が「両側検定 : p=3e-14.0000 ** (p<.01)」と表示されてしまうのが笑えるのだが。
> fisher.test(matrix(c(40, 5, 2, 31), 2))
Fisher's Exact Test for Count Data
data: matrix(c(40, 5, 2, 31), 2)
p-value = 3e-14
この例から見ると,「指数表示されたときの上位から小数点の手前までと ".0000"」を表示しているようだ。
スイッチを反転しても同じ数だけ点灯する?
締め切りが 2017/11/07 10:00 AM なので,その 1 分後に投稿されるように予約
設問
家庭に必ずある分電盤。その中にはブレーカーがあり、家庭内の電気スイッチやコンセントなどにつながっています。
ここでは、1つのブレーカーが2つのスイッチにつながっているものとします。
また、それぞれのスイッチに対して電球が1つずつ付いています。
スイッチをONにしても、そのスイッチにつながるブレーカーでONになっていないと電球は点灯しません。
もちろん、ブレーカーがONになっていても、スイッチがONになっていないと電球は点灯しません。
今、m 個のブレーカーがあり、n 個の電球が点灯しています。
ここで、すべてのスイッチを反転させたとき、点灯している電球の数が同じでした。
(あくまでもスイッチ部分の反転のみで、ブレーカーを触ることはありません。)
このようなブレーカー、スイッチの状態が何通りあるか求めます。
例えば、m = 2, n = 1 のとき、以下のような16通りがあります。
(色が付いている部分が点灯している部分)
同様に、m = 3, n = 2 のときは72通りがあります。
標準入力から m, n がスペース区切りで与えられたとき、上記のような状態が何通りあるか求め、
そのパターン数を標準出力に出力してください。
なお、m, n はともに20以下の正の整数とします。
【入出力サンプル】
標準入力
2 1
標準出力
16
=======================================================
m, n の小さい場合に対するプログラム(最後尾に記載)により,下図の配列 b を得る。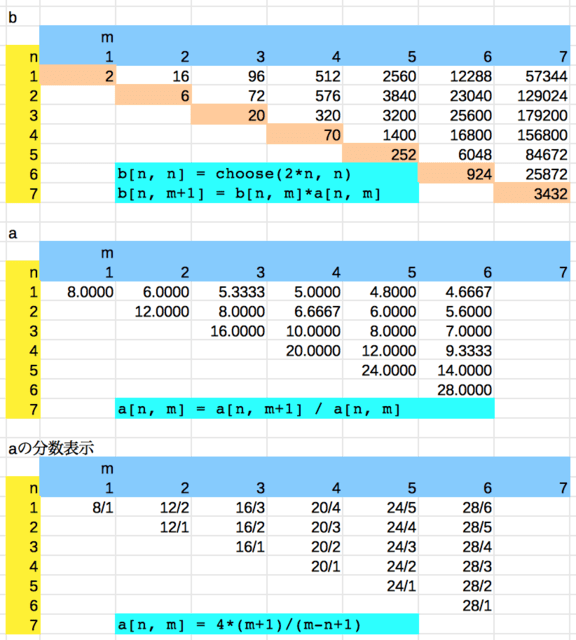
配列 b の対角成分 b[n, n] は choose(2*n, n)
n 行において b[n, m+1] = b[n, m] * a[n, m ]
配列 a は,分数表示すると,規則性があることがわかる。
a[n, m ] = 4*(m+1)/(m-n+1)
これをプログラム化する(面倒くさいので,m = n = 20 までの全てについて表を作る)。
f = function(M, N) {
options(scipen=100)
mx = 20
b = a = matrix(0, mx, mx)
for (m in 1:mx) {
for (n in m:1) {
a[n, m] = 4*(m+1)/(m-n+1)
}
}
for (n in 1:mx) {
b[n, n] = x = choose(2*n, n)
if (n < mx) {
for (m in n:(mx-1)) {
b[n, m+1] = b[n, m]*a[n, m]
}
}
}
cat(b[N, M])
}
f(2, 1) # 16
f(3, 2) # 72
f(10, 5) # 65028096
f(16, 15) # 9927521280
f(20, 20) # 137846528820
小規模な配列 b を求めるプログラム
f = function(m, n) {
library(e1071)
a = bincombinations(3*m)
count = 0
for (j in 1:nrow(a)) {
N1 = N2 = 0
for (i in 1:m) {
N1 = N1+sum(a[j, i]*a[j, m+2*i-1:0])
N2 = N2+sum(a[j, i]*(1-a[j, m+2*i-1:0]))
}
count = count + (N1 == N2 && N1 == n)
}
count
}
作詞支援ツールを作ろう
締め切りが 2017/11/04 10:00 AM なので,その 1 分後に投稿されるように予約
設問
あなたが所属しているプロジェクトでは、様々な楽曲を扱っていましたが、ある日作詞家から作詞支援ツールの開発を依頼されました。
それは、特定の言葉と同じ韻を踏む(母音が一致している)言葉を探すというもので、例えば「試合(SIAI)」と「気合(KIAI)」というように、 特にヒップホップでは欠かせない要素です。
もちろん、実際の曲作りはこんな定石に従うとは限りませんが、まずは「隗より始めよ」ということで、手始めとして入力された文から母音を抽出するプログラムを作ることになりました。
求められるプログラムの前提条件は、以下の通りとなります。
・ 標準入力から、ひらがなのみで構成された文が一行送られる
・ 文字コードとしてUTF-8を想定する
・ 入力文は、1文字以上32文字以下とし、後述する表に定める文字コードのひらがな以外は含まない
・ 入力文から促音である「っ」を取り除いたうえで、ローマ字(Wikipediaへのリンク)に変換し、母音のみを抽出する
・ 母音のみの抽出となるため、ローマ字の種類は訓令式かヘボン式か問わないものとする
・ 母音のみの抽出となるため、撥音「ん」は無視して構わない
・ “てぃ”など、ローマ字の種類によって未定義の文字は入力に含まれないものとする
・ 母音は小文字のアルファベット(a/i/u/e/o)として扱うこと
・ 抽出した母音を連結し、1つの文字列として標準出力に返すこと
ここで、入力として想定される文字コード(UTF-8)とひらがなの対応は以下になります
そして以下が、入力と出力例になります。
作詞支援というのは奥の深いテーマで、今回取り上げた語呂以外にも、”意味の近い単語を探したい”など実際のニーズは様々です。
ただ一方で、既存サービスはいくつかありながらも、決定版といえるようなものがまだ世の中に存在しないのも事実です。
特に、個人的には”新語の対応”が課題と感じています…
この問題をきっかけに、世の中にはこんなニーズがあるんだということを知ってもらい、挑戦者の皆様が今後何か新しいサービスを開発する上でのヒントになれば幸いです。
【問題】
標準入力から、ひらがなのみで構成された文が一行送られます。
この文から、促音を取り除いた上でローマ字に変換し、母音のみ(a/i/u/e/o)を抽出して、その結果を連続した文字列として標準出力に返してください。
================================================================================
f = function(s) {
boin = c("a", "a", "i", "i", "u", "u", "e", "e", "o", "o", "a", "a", "i", "i", "u", "u",
"e", "e", "o", "o", "a", "a", "i", "i", "u", "u", "e", "e", "o", "o", "a", "a", "i",
"i", "u", "u", "u", "e", "e", "o", "o", "a", "i", "u", "e", "o", "a", "a", "a", "i",
"i", "i", "u", "u", "u", "e", "e", "e", "o", "o", "o", "a", "i", "u", "e", "o", "a",
"a", "u", "u", "o", "o", "a", "i", "u", "e", "o", "a", "a", "o", "o", "o")
s = gsub(".([ゃゅょ])", "\\1", gsub("ん", "", gsub("っ", "", s)))
i = utf8ToInt(s) - 12352
cat(paste(boin[i], collapse = ""))
}
# f(readLines(file("stdin", "r")))
f("さとう")
f("しょうゆ")
f("にほんしゅ")
f("いんをふむ")


















