算額(その843)
百四 岩手県大船渡市田茂山 根城八幡宮 天保12年(1841)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市. http://www.wasan.jp/yamamura/yamamura.html
一関市博物館>>和算に挑戦>>平成20年度出題問題&回答例
https://www.city.ichinoseki.iwate.jp/museum/wasan/h20/index.html
全円内に直角三角形が内接し,小円は直角三角形に内接し,大円は直角三角形の二辺と全円に内接している。小円の直径が 1 のとき,大円の直径はいかほどか。
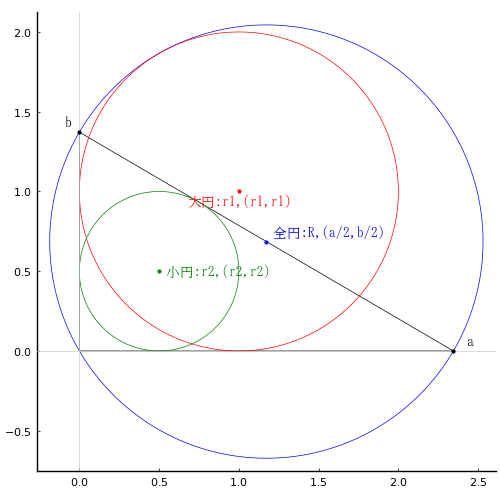
直角三角形が全円に内接するので,全円の中心は直角三角形の斜辺の中点にある。
直角三角形の直角の頂点を原点とし,直角を挟む二辺の短い方を a, 長い方を b
全円の半径と中心座標を R, (a/2, b/2)
大円の半径と中心座標を r1, (r1, r1)
小円の半径と中心座標を r2, (r2, r2)
とおき,以下の連立方程式を解く。
include("julia-source.txt")
using SymPy
@syms a::positive, b::positive, r1::positive, r2::positive, R::positive;
@syms a, b, r1, r2, R
R = sqrt(a^2 + b^2)/2
eq1 = (r1 - a/2)^2 + (r1 - b/2)^2 - (R - r1)^2 |> expand
eq2 = a + b - 2R - 2r2 |> expand
eq3 = (a + b + 2R)r2 - a*b |> expand;
println(eq1, ", # eq1")
println(eq2, ", # eq2")
println(eq3, ", # eq3")
-a*r1 - b*r1 + r1^2 + r1*sqrt(a^2 + b^2), # eq1
a + b - 2*r2 - sqrt(a^2 + b^2), # eq2
-a*b + a*r2 + b*r2 + r2*sqrt(a^2 + b^2), # eq3
注目すべきは,eq1 は r1 について,eq2, eq3 は r2 についての式になっている。つまり単なる一元方程式である。
それぞれについて解く。
res_r1 = solve(eq1, r1)[2] |> factor
res_r1 |> println
a + b - sqrt(a^2 + b^2)
res_r2 = solve(eq2, r2)[1] |> factor
res_r2 |> println
(a + b - sqrt(a^2 + b^2))/2
大円の半径 res_r1 は,小円の半径 res_r2 の 2 倍である。
また,それぞれは直角三角形の直角を挟む二辺 a, b がどんな値であっても,a + b - sqrt(a^2 + b^2) により決まる。
r2 = 1//2 のとき,b = (a - 1/2)/(a - 1) である。例えば a = 3 なら b = 5/4,a = 2.345 なら b = 1.3717472118959106 である。
@syms a
r2 = 1//2
eq = (a + b - sqrt(a^2 + b^2))/2 - r2
solve(eq, b) # a から,r2 = 1/2 になるような b を求める式
1-element Vector{Sym{PyCall.PyObject}}:
(a - 1/2)/(a - 1)
例えば,a = 2.345, b = 1.3717472118959106 のとき,小円の直径は 1,大円の直径は 2 である。
r1 = 1; r2 = 0.5; a = 2.345; b = 1.37175; R = 1.35837
function draw(a, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
b = (a - 1/2)/(a - 1)
r2 = (a + b - sqrt(a^2 + b^2))/2
r1 = 2r2
R = sqrt(a^2 + b^2)/2
@printf("r1 = %g; r2 = %g; a = %g; b = %g; R = %g\n", r1, r2, a, b, R)
plot([0, a, 0, 0], [0, 0, b, 0], color=:black, lw=0.5)
circle(a/2, b/2, R, :blue)
circle(r1, r1, r1)
circle(r2, r2, r2, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(a/2, b/2, "全円:R,(a/2,b/2)", :blue, :left)
point(r1, r1, "大円:r1,(r1,r1)", :red, :center, delta=-delta/2)
point(r2, r2, " 小円:r2,(r2,r2)", :green, :left, :vcenter)
point(a, 0, " a", :black, :left, :bottom, delta=delta/2)
point(0, b, "b ", :black, :right, :bottom, delta=delta/2)
end
end;