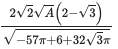算額(その667)
長野市元善町 善光寺 寛政8年(1796)
中村信弥「改訂増補 長野県の算額」(p.56)
http://www.wasan.jp/zoho/zoho.html
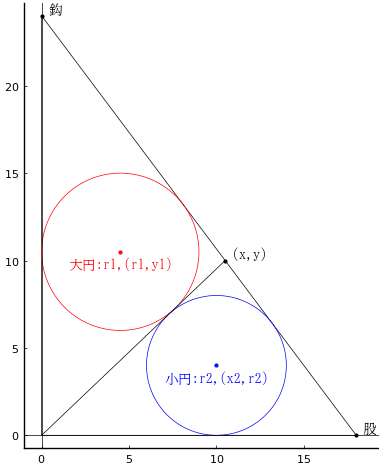
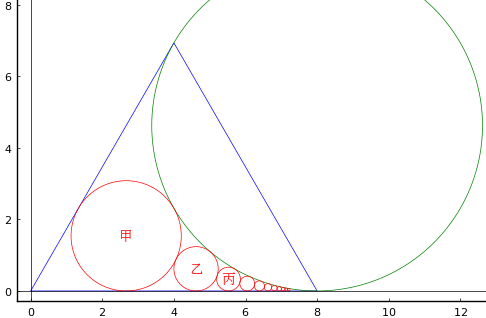
台形内に甲円が内接する直角三角形を入れる。乙円,丙円も台形の辺と直角三角形の辺に内接する。甲円,乙円,丙円の直径がそれぞれ 20寸,24寸,10寸のとき,甲円が内接する直角三角形の直覚を挟む二辺のうち短い方の辺(鈎)の長さはいかほどか。
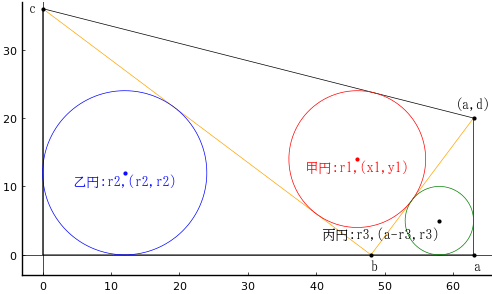
甲円が内接する直角三角形の頂点座標を (b, 0), (0, c), (a, d) とする。
甲円の半径と中心座標を r1, (x1, y1)
乙円の半径と中心座標を r2, (r2, r2)
丙円の半径と中心座標を r3, (a - r3, r3)
とおき,以下の連立方程式を解く。
求めるべき,「甲円が内接する直角三角形の直覚を挟む二辺のうち短い方の辺(鈎)の長さ」は (b, 0), (a, d) を端点とする直線の長さ sqrt((a - b)^2 + d^2) である。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms a::positive, b::positive, c::positive, d::positive,
x1::positive, y1::positive,
r1::positive, r2::positive, r3::positive,
鈎::positive, 股::positive, 弦::positive
弦 = sqrt(a^2 + (c - d)^2)
鈎 = sqrt((a - b)^2 + d^2)
股 = sqrt(b^2 + c^2)
eq1 = 鈎^2 + 股^2 - 弦^2 |> simplify
eq2 = 鈎 + 股 - 弦 - 2r1
eq3 = b + c - 股 - 2r2
eq4 = d + (a - b) - 鈎 -2r3
eq5 = dist(0, c, a, d, x1, y1) - r1^2
eq6 = dist(b, 0, a, d, x1, y1) - r1^2;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (a, b, c, d, x1, y1))
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(a, b, c, d, x1, y1) = u
return [
-2*a*b + 2*b^2 + 2*c*d, # eq1
-2*r1 - sqrt(a^2 + (c - d)^2) + sqrt(b^2 + c^2) + sqrt(d^2 + (a - b)^2), # eq2
b + c - 2*r2 - sqrt(b^2 + c^2), # eq3
a - b + d - 2*r3 - sqrt(d^2 + (a - b)^2), # eq4
-r1^2 + (-a*(a*x1 + (-c + d)*(-c + y1))/(a^2 + (-c + d)^2) + x1)^2 + (-c + y1 - (-c + d)*(a*x1 + (-c + d)*(-c + y1))/(a^2 + (-c + d)^2))^2, # eq5
-r1^2 + (-d*(d*y1 + (a - b)*(-b + x1))/(d^2 + (a - b)^2) + y1)^2 + (-b + x1 - (a - b)*(d*y1 + (a - b)*(-b + x1))/(d^2 + (a - b)^2))^2, # eq6
]
end;
(r1, r2, r3) = (20, 24, 10) .// 2
iniv = BigFloat[59, 46, 37, 22, 43, 15]
res = nls(H, ini=iniv)
(BigFloat[63.00000000000000000000000000000000000000000000000000000000000000635922298913147, 48.00000000000000000000000000000000000000000000000000000000000001088653549950012, 35.99999999999999999999999999999999999999999999999999999999999998913806908318885, 20.00000000000000000000000000000000000000000000000000000000000000452357741848939, 46.00000000000000000000000000000000000000000000000000000000000000725087619460416, 13.99999999999999999999999999999999999999999999999999999999999999999791841656566], true)
「甲円が内接する直角三角形の直覚を挟む二辺のうち短い方の辺(鈎)の長さ」は (b, 0), (a, d) を端点とする線分の長さ sqrt((a - b)^2 + d^2) である。
a = 63, b = 48, d = 20 なので,線分の長さは 25 である。
その他のパラメータは以下の通りである。
a = 63; b = 48; c = 36; d = 20; x1 = 46; y1 = 14
鈎 = 25; 股 = 60; 弦 = 65
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(a, b, c, d, x1, y1) = res[1]
@printf("a = %g; b = %g; c = %g; d = %g; x1 = %g; y1 = %g\n", a, b, c, d, x1, y1)
鈎 = sqrt((a - b)^2 + d^2)
股 = sqrt(b^2 + c^2)
弦 = sqrt(a^2 + (c - d)^2)
@printf("鈎 = %g; 股 = %g; 弦 = %g\n", 鈎, 股, 弦)
plot([0, a, a, 0, 0], [0, 0, d, c, 0], color=:black, lw=0.5)
plot!([0, b, a], [c, 0, d], color=:orange, lw=0.5)
circle(x1, y1, r1)
circle(r2, r2, r2, :blue)
circle(a - r3, r3, r3, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
point(x1, y1, "甲円:r1,(x1,y1)", :red, :center, delta=-delta/2)
point(r2, r2, "乙円:r2,(r2,r2)", :blue, :center, delta=-delta/2)
point(a - r3, r3, "丙円:r3,(a-r3,r3)", :black, :right, delta=-2delta)
point(a, 0, " a", :black, :center, delta=-1.5delta)
point(b, 0, " b", :black, :center, delta=-1.5delta)
point(0, c, "c ", :black, :right, :vcenter)
point(a, d, "(a,d)", :black, :center, :bottom, delta=2delta)
plot!(xlims=(-3, 66), ylims=(-3, 37))
end
end;