算額(その523)
和算図形問題あれこれ - 令和4年11月の問題-No.1
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html
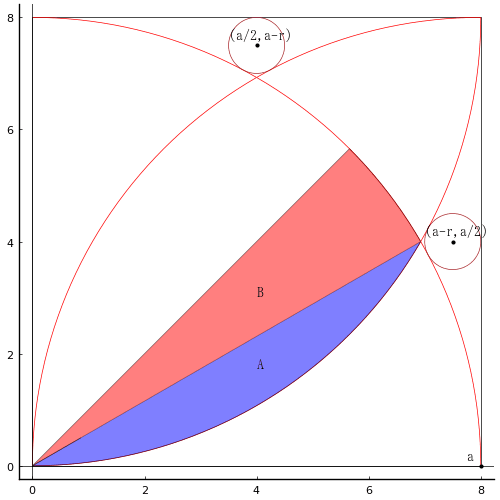
2 個の甲円が交差しており,乙円 2 個と丙円 3 個が入っている。甲円,丙円の直径が 100 寸,36 寸であるとき,乙円の直径はいくらか。

甲円の半径と中心座標を r1, (0, r1 - r3), (0, r3 - r1)
乙円の半径と中心座標を r2, (x2, y2)
丙円の半径と中心座標を r3, (x3, y3), (0, 0)
とおき,以下の連立方程式を解く。
なお,r1, r3 を変数のままとして解くことは,solve() の性能上無理なようで,問に書かれた通りの数値を代入して解を求める。
include("julia-source.txt");
using SymPy
@syms r1::positive, r2::positive, x2::negative, y2::positive,
r3::positive, x3::positive, y3::positive;
(r1, r3) = (100, 36) .// 2
eq1 = x2^2 + (y2 - (r3 - r1))^2 - (r1 + r2)^2
eq2 = x3^2 + (y3 - (r3 - r1))^2 - (r1 + r3)^2
eq3 = x2^2 + (y2 - (r1 - r3))^2 - (r1 - r2)^2
eq4 = x3^2 + (y3 - (r1 - r3))^2 - (r1 - r3)^2
eq5 = (x3 - x2)^2 + (y3 - y2)^2 - (r2 + r3)^2;
res = solve([eq1, eq2, eq3, eq4, eq5], (r2, x2, y2, x3, y3))
1-element Vector{NTuple{5, Sym}}:
(20500*sqrt(7)/4181 + 72242/4181, -66075*sqrt(41)/16724 + 25215*sqrt(287)/33448, 128125*sqrt(7)/16724 + 903025/33448, 15*sqrt(287)/8, 225/8)
乙円の半径 r2 は 20500√7/4181 + 72242/4181 = 82*(250√7 + 881)/4181,直径は 60.502225246029234 である。
2*82*(250√7 + 881)/4181
60.502225246029234
r2 = 30.2511; x2 = -12.527; y2 = 47.2674; x3 = 31.7645; y3 = 28.125
乙円の直径 = 60.5022
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r3) = (100, 36) .// 2
(r2, x2, y2, x3, y3) = res[1]
#r2 = 4.30617; x2 = 38.0693; y2 = 6.72839; x3 = 31.7645; y3 = 28.125
@printf("r2 = %g; x2 = %g; y2 = %g; x3 = %g; y3 = %g\n", r2, x2, y2, x3, y3)
@printf("乙円の直径 = %g\n", 2r2)
plot()
circle(0, r1 - r3, r1)
circle(0, r3 - r1, r1)
circle(x2, y2, r2, :blue)
circle(-x2, -y2, r2, :blue)
circle(x3, y3, r3, :green)
circle(-x3, -y3, r3, :green)
circle(0, 0, r3, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(0, r1 - r3, "甲円:r1 \n(0,r1-r3) ", :red, :right, :vcenter)
point(0, r3 - r1, "(0,r3-r1)")
point(x2, y2, "乙円:r2 \n(x2,y2) ", :blue, :right, :vcenter)
point(x3, y3, " 丙円:r3(x3,y3)", :green, :center, :top, delta=-delta/2)
end
end;