算額（その871）

算額（その871）

(3) 奈良県大和郡山市小泉町 耳成山口神社 嘉永7年(1854)
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.

奈良県大和郡山市 庚申堂 明治13年(1880)
http://www.wasan.jp/nara/kosindo.html

牧下英世：数学教育を通して取り組んだ総合的な学習とその実証的な研究-算額を―算額を用いた課題学習とそのフィールドワークの実践から―，2002筑波大学附属駒場論集第42集
https://tsukuba.repo.nii.ac.jp/record/6466/files/13.pdf

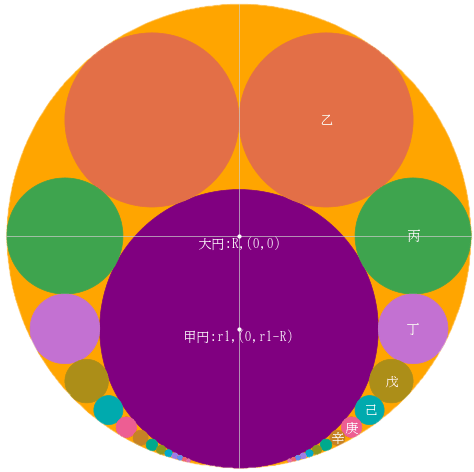
大円と小円が交差してできる隙間に甲円から始まる累円を入れる。
大円，小円，甲円の直径をそれぞれ 7 尺 2 寸，6 尺 1 寸，1 尺 7 寸としたとき，乙円，丙円，丁円，戊円の直径を求めよ。

大円の半径と中心座標を R1, (0, 0)
小円の半径と中心座標を R2, (0, 2r1 - R1 + R2)
甲円の半径と中心座標を r1, (0, r1 - R1)
乙円の半径と中心座標を r2, (x2, y2)
丙円の半径と中心座標を r3, (x3, y3)
:

include("julia-source.txt");

using SymPy
@syms R1, R2, r1, r2, x2, y2

(R1, R2, r1) = (72, 61, 17) .// 2
eq1 = x2^2 + y2^2 - (R1 -r2)^2
eq2 = x2^2 + (2r1 - R1 + R2 - y2)^2 - (R2 + r2)^2
eq3 = x2^2 + (y2 - r1 + R1)^2 - (r1 + r2)^2
#(r2, x2, y2) = 
solve([eq1, eq2, eq3], (r2, x2, y2))[2]

   (36465/4681, 204*sqrt(130845)/4681, -109509/4681)

漸化式的に累円のパラメータを数式で求めることが SymPy では困難なので，関数内で solve() を使う，半自動的なやり方を取る。
一つの累円のパラメータが得られたら，それを関数の引数に指定して，次の累円のパラメータを得る。
注意点として（Julia の SymPy 特有であるが），xx/yy の分数は xx//yy にすることと，sqrt(zz) は sqrt(Sym(zz)) にすること。そのようにしなくても良いが，処理時間がかかる。

function nextcircle(R1, R2, r1, r2, x2, y2)
   @syms r3, x3, y3
   eq4 = x3^2 + y3^2 - (R1 -r3)^2
   eq5 = x3^2 + (2r1 - R1 + R2 - y3)^2 - (R2 + r3)^2
   eq6 = (x3 - x2)^2 + (y3 - y2)^2 - (r2 + r3)^2;
   solve([eq4, eq5, eq6], (r3, x3, y3))
end;

# r3
nextcircle(R1, R2, r1, 36465//4681, 204*sqrt(Sym(130845))/4681, -109509//4681)

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (8690825/1404066, 50932*sqrt(130845)/702033, -19854559/1404066)
    (17/2, 0, -55/2)

# r4
nextcircle(R1, R2, r1, 8690825//1404066, 50932*sqrt(Sym(130845))/702033, -19854559//1404066)

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (18641819625/4108026529, 353486916*sqrt(130845)/4108026529, -18850643421/4108026529)
    (36465/4681, 204*sqrt(130845)/4681, -109509/4681)

# r5
nextcircle(R1, R2, r1, 18641819625//4108026529, 353486916*sqrt(Sym(130845))/4108026529, -18850643421//4108026529)

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (4442967010625/1379049831714, 62216188328*sqrt(130845)/689524915857, 4167487120889/1379049831714)
    (8690825/1404066, 50932*sqrt(130845)/702033, -19854559/1404066)

# r6
nextcircle(R1, R2, r1, 4442967010625//1379049831714, 62216188328*sqrt(Sym(130845))/689524915857, 4167487120889//1379049831714)

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (9530164237790625/4195069355668441, 378487752059964*sqrt(130845)/4195069355668441, 35723160673770891/4195069355668441)
    (18641819625/4108026529, 353486916*sqrt(130845)/4108026529, -18850643421/4108026529)

# r7
nextcircle(R1, R2, r1, 9530164237790625//4195069355668441, 378487752059964*sqrt(Sym(130845))/4195069355668441, 35723160673770891//4195069355668441)

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (2271355810006765625/1413029171738162306, 62689304552989212*sqrt(130845)/706514585869081153, 17460791512813260881/1413029171738162306)
    (4442967010625/1379049831714, 62216188328*sqrt(130845)/689524915857, 4167487120889/1379049831714)

# r8
nextcircle(R1, R2, r1, 2271355810006765625//1413029171738162306, 62689304552989212*sqrt(Sym(130845))/706514585869081153, 17460791512813260881//1413029171738162306)

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (4872058212464512265625/4255498594259851496689, 369959068275411941556*sqrt(130845)/4255498594259851496689, 63967589464505474522739/4255498594259851496689)
    (9530164237790625/4195069355668441, 378487752059964*sqrt(130845)/4195069355668441, 35723160673770891/4195069355668441)

累円の直径と中心座標は以下のようになる。算額の答えとはずいぶん異なる。

乙円: 直径 = 15.58000, (15.7641, -23.3944)
丙円: 直径 = 12.37951, (26.2429, -14.1408)
丁円: 直径 =  9.07580, (31.1257, -4.58873)
戊円: 直径 =  6.44352, (32.6386,  3.02200)
己円: 直径 =  4.54351, (32.6356,  8.51551)
庚円: 直径 =  3.21487, (32.0960, 12.35700)
辛円: 直径 =  2.28977, (31.4472, 15.03170)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   names = Char["甲乙丙丁戊己庚辛壬癸"...]
   (R1, R2, r1) = (72, 61, 17) .// 2
   plot(showaxis=false)
   delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
   circlef(0, 0, R1, :lightgreen)
   circlef(0, 2r1 - R1 + R2, R2, :cadetblue1)
   circle(0, 2r1 - R1 + R2, R2, :lightslateblue)
   circle(0, 0, R1, :mediumseagreen)
   circlef(0, r1 - R1, r1, :gold)
   number = 1
   for (r, x, y) in [
       (7.790002136295663, 15.764133064156171, -23.394360179448835)
       (6.189755324892134, 26.242896581838256, -14.140759052637128)
       (4.537901470061319, 31.12566720233952, -4.588734587745892)
       (3.221759582902747, 32.63863611252851, 3.021998933649333)
       (2.2717536779012537, 32.63557363626892, 8.515511340831878)
       (1.607437309459633, 32.095998094235, 12.356992949646468)
       (1.1448854005113114, 31.447186145793232, 15.031749640521548)]
       number += 1
       circlef(x, y, r, number)
       circlef(-x, y, r, number)
       point(x, y, names[number], :white, :center, :vcenter, mark=false)
       @printf("%s円: 直径 = %8.5f, (%g, %g)\n", names[number], 2r, x, y)
   end
   if more        
       #hline!([0], color=:gray80, lw=0.5)
       #vline!([0], color=:gray80, lw=0.5)
       point(0, 0, "大円:R1,(0,0)", :red, :center, delta=-1)
       point(0, 2r1 - R1 + R2, "小円:R2,(0,2r1-R1+R2)", :green, :center, delta=-1)
       point(0, r1 - R1, " 甲円:r1\n(0,r1-R1)", :white, :center, delta=-1)
   end
end;

算額（その870）

算額（その870）

奈良県大和郡山市 庚申堂 明治13年(1880)
http://www.wasan.jp/nara/kosindo.html

牧下英世：数学教育を通して取り組んだ総合的な学習とその実証的な研究―算額を用いた課題学習とそのフィールドワークの実践から―，2002筑波大学附属駒場論集第42集
https://tsukuba.repo.nii.ac.jp/record/6466/files/13.pdf

(5) 奈良県大和郡山市小泉町 庚申堂
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.

キーワード：円3個，長方形

長方形内に大円，中円，小円を入れる。中円と小円の直径がそれぞれ 4 寸 5 分，2 寸，長方形の長辺と短辺の和が 2 尺 1 寸 2 分 5 厘のとき大円の直径と長方形の長辺と短辺を求めよ。

長方形の長辺と短辺の長さを a, b
大円の半径と中心座標を r1, (r1, r1)
中円の半径と中心座標を r2, (a - r2, r2)
小円の半径と中心座標を r3, (r3, b - r3)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a, b, r1, r2, r3, K
(r2, r3, K) = (45//20, 2//2, 2125//100)
eq1 = (a + b) - K
eq2 = (a - r2 - r1)^2 + (r1 - r2)^2 - (r1 + r2)^2 |> expand
eq3 = (r1 - r3)^2 + (b - r3 - r1)^2 - (r1 + r3)^2 |> expand
res = solve([eq1, eq2, eq3], (r1, a, b))[2]  # 4 組のうち 2 番目

   (4, 49/4, 9)

大円の直径は 8 寸，長方形の長辺と短辺は 12.25 寸と 9 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, r3, K) = (45//20, 2//2, 2125//100)
   (r1, a, b) = (4, 49/4, 9)
   plot([0, a, a, 0, 0], [0, 0, b, b, 0], color=:blue, lw=0.5)
   circle(r1, r1, r1)
   circle(a - r2, r2, r2, :green)
   circle(r3, b - r3, r3, :magenta)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(0, b, " b", :blue, :left, :bottom, delta=delta/2)
       point(r1, r1, "大円:r1,(r1,r1)", :red, :center, delta=-delta/2)
       point(a - r2, r2, "中円:r2,(a-r2,r2)", :green, :center, delta=-delta/2)
       point(r3, b - r3, " 小円:r3,(r3,b-r3)", :magenta, :left, :bottom, delta=delta/2)
   end
end;

算額（その869）

算額（その869）

奈良県大和郡山市 庚申堂 明治13年(1880)
http://www.wasan.jp/nara/kosindo.html

牧下英世：数学教育を通して取り組んだ総合的な学習とその実証的な研究-算額を用いた課題学習とそのフィールドワークの実践から-，2002筑波大学附属駒場論集第42集
https://tsukuba.repo.nii.ac.jp/record/6466/files/13.pdf

直角三角形内に斜線を引き，2 個の等円を入れる。直角三角形の底辺（股），高さ（鈎）がそれぞれ 4 寸，3 寸のとき，等円の直径と斜線の長さを求めよ。

鈎，股 を b, a
斜線と股の交点座標を (c, 0)
等円の半径と中心座標を r, (r, r), (x, r)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms d, a, b, c, r, x
eq1 = numerator(apart(dist(a, 0, 0, b, x, r) - r^2, d))
eq2 = numerator(apart(dist(c, 0, 0, b, x, r) - r^2, d))
eq3 = (b + c - 2r)^2 - (b^2 + c^2);  # b + c - sqrt(b^2 + c^2) - 2r
(c, x, r) = solve([eq1, eq2, eq3], (c, x, r))[8]  # 8 組中 8 番目
c |> println
x |> println
r |> println

   sqrt(b*(-a + sqrt(a^2 + b^2)))*(a - b + sqrt(a^2 + b^2))/(2*b)
   (a^2*b - a^2*sqrt(b*(-a + sqrt(a^2 + b^2))) - a*b^2/2 + a*b*sqrt(b*(-a + sqrt(a^2 + b^2)))/2 - a*b*sqrt(a^2 + b^2) + a*sqrt(b*(-a + sqrt(a^2 + b^2)))*sqrt(a^2 + b^2) + b^3/2 - b^2*sqrt(b*(-a + sqrt(a^2 + b^2)))/2 - b^2*sqrt(a^2 + b^2)/2 + b*sqrt(b*(-a + sqrt(a^2 + b^2)))*sqrt(a^2 + b^2)/2)/(a*b - 2*a*sqrt(b*(-a + sqrt(a^2 + b^2))) + b^2 - b*sqrt(a^2 + b^2))
   b/2 - sqrt(-a*b/4 + b*sqrt(a^2 + b^2)/4)

等円の直径は，2r = 1.2679491924311228 寸

2r(a => 4, b => 3) |> N

   1.2679491924311228

斜線の長さは，sqrt(b^2 + c^2) = 3.4641016151377544 寸

sqrt(b^2 + c^2)(a => 4, b => 3) |> N

   3.4641016151377544

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b) = (4, 3)
   c = sqrt(b*(-a + sqrt(a^2 + b^2)))*(a - b + sqrt(a^2 + b^2))/(2*b)
   x = (a^2*b - a^2*sqrt(b*(-a + sqrt(a^2 + b^2))) - a*b^2/2 + a*b*sqrt(b*(-a + sqrt(a^2 + b^2)))/2 - a*b*sqrt(a^2 + b^2) + a*sqrt(b*(-a + sqrt(a^2 + b^2)))*sqrt(a^2 + b^2) + b^3/2 - b^2*sqrt(b*(-a + sqrt(a^2 + b^2)))/2 - b^2*sqrt(a^2 + b^2)/2 + b*sqrt(b*(-a + sqrt(a^2 + b^2)))*sqrt(a^2 + b^2)/2)/(a*b - 2*a*sqrt(b*(-a + sqrt(a^2 + b^2))) + b^2 - b*sqrt(a^2 + b^2))
   r = b/2 - sqrt(-a*b/4 + b*sqrt(a^2 + b^2)/4)
   plot([0, a, 0, 0], [0, 0, b, 0], color=:blue, lw=0.5)
   circle(r, r, r)
   circle(x, r, r)
   segment(c, 0, 0, b, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, "a", :blue, :left, :bottom, delta=delta/2)
       point(c, 0, "c ", :blue, :right, :bottom, delta=delta/2)
       point(0, b, "b", :blue, :left, :bottom, delta=delta/2)
       point(r, r, "等円:r,(r,r)", :red, :center, delta=-delta/2)
       point(x, r, "等円:r,(x,r)", :red, :center, delta=-delta/2)
   end
end;

算額（その868）

算額（その868）

奈良県大和郡山市 庚申堂 明治13年(1880)
http://www.wasan.jp/nara/kosindo.html

牧下英世：数学教育を通して取り組んだ総合的な学習とその実証的な研究-算額を―算額を用いた課題学習とそのフィールドワークの実践から―，2002筑波大学附属駒場論集第42集
https://tsukuba.repo.nii.ac.jp/record/6466/files/13.pdf

"たばや"の算額
https://www.libe.nara-k.ac.jp/~yano/ketcindy/sangaku_tabaya.html

大円の中に，甲円と乙円を入れる。大円に接し，甲円と乙円に外接する丙円を描く。次に，大円に接し，甲円と丙円に外接する丁円を描く。同じ手順で，戊円，己円...を描くことができる。大円，甲円の直径がそれぞれ 16 寸，9.6 寸のとき，乙円，丙円，丁円の直径を求めよ。

大円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, r1 - R)
乙円の半径と中心座標を r2, (x2, y2); x2 = r2
丙円の半径と中心座標を r3, (x3, y3)
丁円の半径と中心座標を r4, (x4, x5)
とおき，以下のように方程式を解いてゆく。

1.　乙円の半径と中心座標を求める

大円と甲円の半径が既知なので，乙円の半径と中心座標は次の二元連立方程式を解けばよい。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive,
     r2::positive, x2::positive, y2::positive

x2 = r2
eq1 = r2^2 + y2^2 - (R - r2)^2
eq2 = r2^2 + (y2 - r1 + R)^2 - (r1 + r2)^2
res1 = solve([eq1, eq2], (r2, y2))[1]

   (-(-R + r1)*(R + (-R^2 + 3*R*r1)/(R + r1))/(R + r1), (-R^2 + 3*R*r1)/(R + r1))

2.　丙円の半径と中心座標を求める

乙円までは半径と中心座標が決まったので，次の累円（丙円）の半径と中心座標は次の三元連立方程式を解けばよい。

@syms r3::positive, x3::positive, y3::real

eq3 = x3^2 + y3^2 - (R - r3)^2
eq4 = x3^2 + (y3 - r1 + R)^2 - (r1 +r3)^2
eq5 = (x2 - x3)^2 + (y2 - y3)^2 - (r2 + r3)^2;
res2 = solve([eq3, eq4, eq5], (r3, x3, y3));
# res2[1]

2 組の解が得られるが，2 番目のものが適解である。
求める累円の前にある累円（甲円）の半径と中心座標から，求めるべき累円（乙円）の半径と中心座標が得られる。
この関係式は前の累円と次の累円の関係式なので，次々に適用することで，累円の半径と中心座標を決定していくことができる。

3.　丙円以降の半径と中心座標を求める

これを関数にすると以下のようなものになる。

nextcircle(R, r1, r2, x2, y2) = ((R^6 - R^5*r1 + R^5*r2 + 3*R^5*y2 - R^4*r1^2 - R^4*r1*r2 - R^4*r1*y2 - R^4*r2^2 + 2*R^4*r2*y2 + R^4*x2^2 + 3*R^4*y2^2 + R^3*r1^3 - R^3*r1^2*r2 - 3*R^3*r1^2*y2 + R^3*r1*r2^2 - 2*R^3*r1*r2*y2 + 3*R^3*r1*x2^2 + R^3*r1*y2^2 - R^3*r2^3 - R^3*r2^2*y2 + R^3*r2*x2^2 + R^3*r2*y2^2 + R^3*x2^2*y2 + R^3*y2^3 - 2*R^2*sqrt(r1)*x2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + R^2*r1^3*r2 + R^2*r1^3*y2 + R^2*r1^2*r2^2 - 2*R^2*r1^2*r2*y2 - R^2*r1^2*x2^2 - 3*R^2*r1^2*y2^2 + R^2*r1*r2^3 - R^2*r1*r2^2*y2 - R^2*r1*r2*x2^2 - R^2*r1*r2*y2^2 + R^2*r1*x2^2*y2 + R^2*r1*y2^3 - R*r1^3*r2^2 + 2*R*r1^3*r2*y2 - 3*R*r1^3*x2^2 - R*r1^3*y2^2 + R*r1^2*r2^3 + R*r1^2*r2^2*y2 - R*r1^2*r2*x2^2 - R*r1^2*r2*y2^2 - R*r1^2*x2^2*y2 - R*r1^2*y2^3 + 2*r1^(5/2)*x2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) - r1^3*r2^3 + r1^3*r2^2*y2 + r1^3*r2*x2^2 + r1^3*r2*y2^2 - r1^3*x2^2*y2 - r1^3*y2^3)/(2*(R^5 - R^4*r1 + 2*R^4*r2 + 2*R^4*y2 - R^3*r1^2 - 2*R^3*r1*r2 + 2*R^3*r1*y2 + R^3*r2^2 + 2*R^3*r2*y2 + R^3*y2^2 + R^2*r1^3 - 2*R^2*r1^2*r2 - 2*R^2*r1^2*y2 - R^2*r1*r2^2 + 2*R^2*r1*r2*y2 + 4*R^2*r1*x2^2 + 3*R^2*r1*y2^2 + 2*R*r1^3*r2 - 2*R*r1^3*y2 - R*r1^2*r2^2 - 2*R*r1^2*r2*y2 + 4*R*r1^2*x2^2 + 3*R*r1^2*y2^2 + r1^3*r2^2 - 2*r1^3*r2*y2 + r1^3*y2^2)), (R^3*sqrt(r1)*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + 2*R^3*r1^2*x2 - 2*R^3*r1*r2*x2 + 2*R^3*r1*x2*y2 + R^2*sqrt(r1)*r2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + R^2*sqrt(r1)*y2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + 2*R^2*r1^3*x2 - 2*R^2*r1*r2^2*x2 + 2*R^2*r1*x2^3 + 2*R^2*r1*x2*y2^2 - R*r1^(5/2)*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + 2*R*r1^(3/2)*y2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + 2*R*r1^3*r2*x2 - 2*R*r1^3*x2*y2 - 2*R*r1^2*r2^2*x2 + 2*R*r1^2*x2^3 + 2*R*r1^2*x2*y2^2 - r1^(5/2)*r2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + r1^(5/2)*y2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)))/(R^5 - R^4*r1 + 2*R^4*r2 + 2*R^4*y2 - R^3*r1^2 - 2*R^3*r1*r2 + 2*R^3*r1*y2 + R^3*r2^2 + 2*R^3*r2*y2 + R^3*y2^2 + R^2*r1^3 - 2*R^2*r1^2*r2 - 2*R^2*r1^2*y2 - R^2*r1*r2^2 + 2*R^2*r1*r2*y2 + 4*R^2*r1*x2^2 + 3*R^2*r1*y2^2 + 2*R*r1^3*r2 - 2*R*r1^3*y2 - R*r1^2*r2^2 - 2*R*r1^2*r2*y2 + 4*R*r1^2*x2^2 + 3*R*r1^2*y2^2 + r1^3*r2^2 - 2*r1^3*r2*y2 + r1^3*y2^2), -sqrt(r1)*x2*sqrt(-R*(-R^2 - 2*R*r2 - r2^2 + x2^2 + y2^2)*(R^2 - 2*R*r1 + 2*R*y2 + 2*r1*r2 - 2*r1*y2 - r2^2 + x2^2 + y2^2))*(R + r1)/(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 + R^2*r1^2 - 4*R^2*r1*r2 + R^2*r2^2 + 2*R^2*r2*y2 + R^2*y2^2 + 2*R*r1^2*r2 - 2*R*r1^2*y2 - 2*R*r1*r2^2 + 4*R*r1*x2^2 + 2*R*r1*y2^2 + r1^2*r2^2 - 2*r1^2*r2*y2 + r1^2*y2^2) + (-R^5 + 4*R^4*r1 - 3*R^4*r2 - R^4*y2 - 3*R^3*r1^2 + 8*R^3*r1*r2 + 2*R^3*r1*y2 - 3*R^3*r2^2 - 2*R^3*r2*y2 + R^3*x2^2 + R^3*y2^2 - 5*R^2*r1^2*r2 + 3*R^2*r1^2*y2 + 4*R^2*r1*r2^2 - 4*R^2*r1*x2^2 - R^2*r2^3 - R^2*r2^2*y2 + R^2*r2*x2^2 + R^2*r2*y2^2 + R^2*x2^2*y2 + R^2*y2^3 - R*r1^2*r2^2 + 2*R*r1^2*r2*y2 + 3*R*r1^2*x2^2 - R*r1^2*y2^2 - 2*R*r1*r2^2*y2 + 2*R*r1*x2^2*y2 + 2*R*r1*y2^3 + r1^2*r2^3 - r1^2*r2^2*y2 - r1^2*r2*x2^2 - r1^2*r2*y2^2 + r1^2*x2^2*y2 + r1^2*y2^3)/(2*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 + R^2*r1^2 - 4*R^2*r1*r2 + R^2*r2^2 + 2*R^2*r2*y2 + R^2*y2^2 + 2*R*r1^2*r2 - 2*R*r1^2*y2 - 2*R*r1*r2^2 + 4*R*r1*x2^2 + 2*R*r1*y2^2 + r1^2*r2^2 - 2*r1^2*r2*y2 + r1^2*y2^2)));

順次適用した結果を表示すると以下のようになる。
大円，甲円の直径がそれぞれ 16 寸，9.6 寸 なので，乙円の，半径と中心座標は以下のようになる。

res1

   (-(-R + r1)*(R + (-R^2 + 3*R*r1)/(R + r1))/(R + r1), (-R^2 + 3*R*r1)/(R + r1))

res1[1](R => 16/2, r1 => 9.6/2) |> N  # r2 = x2

   3.0

res1[2](R => 16/2, r1 => 9.6/2) |> N  # y2

   3.999999999999999

nextcircle(16/2, 9.6/2, 3, 3, 4)  # r3, x3, y3

   (2.0000000000000004, 5.999999999999999, 0.0)

nextcircle(16/2, 9.6/2, 2, 6, 0)  # r4, x4, y4

   (1.2000000000000002, 6.000000000000001, -3.2000000000000006)

nextcircle(16/2, 9.6/2, 1.2, 6, -3.2) # r5, x5, y5

   (0.7499999999999988, 5.250000000000001, -4.999999999999999)

nextcircle(16/2, 9.6/2, 0.75, 5.25, -5)  # r6, x6, y6

   (0.5000000000000001, 4.499999999999999, -6.000000000000001)

乙円，丙円，丁円の直径は 2r2 = 6 寸, 2r3 = 4　寸, 2r4 = 2.4 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, r1) = (160, 96) .// 20
   (r2, y2) = (-(-R + r1)*(R + (-R^2 + 3*R*r1)/(R + r1))/(R + r1), (-R^2 + 3*R*r1)/(R + r1))
   x2 = r2
   plot(showaxis=false)
   delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
   circlef(0, 0, R, :orange)
   circlef(0, r1 - R, r1, :purple)
   names = Char["甲乙丙丁戊己庚辛壬癸"...]
   @printf("%g %g %g %g\n", 1, r1, 0, r1 - R)
   for i = 2:15
       @printf("%g %g %g %g\n", i, r2, x2, y2)
       if i <= 8
           notation = @sprintf("%s円:r%g,(x%g,y%g)", names[i], i, i, i)
           point(x2, y2, names[i], :white, :center, :vcenter)
       end
       circlef(x2, y2, r2, i)
       circlef(-x2, y2, r2, i)
       r2, x2, y2 = nextcircle(R, r1, r2, x2, y2)
   end

   if more        
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 0, "大円:R,(0,0)", :white, :center, delta=-2delta)
       point(0, r1 - R, "甲円:r1,(0,r1-R)", :white, :center, delta=-2delta)
   end
end;

   1 4.8 0 -3.2
   2 3 3 4
   3 2 6 0
   4 1.2 6 -3.2
   5 0.75 5.25 -5
   6 0.5 4.5 -6
   7 0.352941 3.88235 -6.58824
   8 0.26087 3.3913 -6.95652
   9 0.2 3 -7.2
   10 0.157895 2.68421 -7.36842
   11 0.12766 2.42553 -7.48936
   12 0.105263 2.21053 -7.57895
   13 0.0882353 2.02941 -7.64706
   14 0.075 1.875 -7.7
   15 0.0645161 1.74194 -7.74194

4.　直径だけを求める場合

累円の直径（半径）だけを逐次求めるには，算法助術の公式55 を使えばよい。

using SymPy
@syms d1, d2, d3, d4, R, r1, r2, r3, r4
(d1, d2, d3) = (R, r1, r2)
eq55 = d1^2*d2^2*d3^2 + d1^2*d4^2*(d2 - d3)^2 + 2*d1*d2^2*d3^2*d4 - 2*d1*d2*d3*d4*(d1 - d4)*(d2 + d3) + d2^2*d3^2*d4^2;

外円 R に内接し，甲円 r1 と i 番目の累円 r(i)に接する r(i+1) 番目の累円の半径 d4 は，eq55 を 解けば求めることができる。

res = solve(eq55, d4)[1]
res |> println

   (R*r1*r2*(R*r1 + R*r2 - r1*r2) - 2*sqrt(-R^3*r1^3*r2^3*(-R + r1 + r2)))/(R^2*r1^2 - 2*R^2*r1*r2 + R^2*r2^2 + 2*R*r1^2*r2 + 2*R*r1*r2^2 + r1^2*r2^2)

これを関数にすれば，（外円，甲円と）乙円を初期値として，次の円の半径を求めることができる。

nxt(R, r1, r2) = (R*r1*r2*(R*r1 + R*r2 - r1*r2) - 2*sqrt(-R^3*r1^3*r2^3*(-R + r1 + r2)))/(R^2*r1^2 - 2*R^2*r1*r2 + R^2*r2^2 + 2*R*r1^2*r2 + 2*R*r1*r2^2 + r1^2*r2^2);

(R, r1) = (160, 96) .// 20
r = 3  # r2 から始める
for i = 2:15
   @printf("%g %g\n", i, r)
   r = nxt(R, r1, r)  # i = 2 のとき r3 が求まる
end

   2 3
   3 2
   4 1.2
   5 0.75
   6 0.5
   7 0.352941
   8 0.26087
   9 0.2
   10 0.157895
   11 0.12766
   12 0.105263
   13 0.0882353
   14 0.075
   15 0.0645161