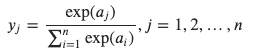Julia の小ネタ--039 Julia で，内包表記で組合せ(コンビネーション)を列挙する

内包表記で組合せ(コンビネーション)を列挙する

Python だと，

　>>> a, b = 5, 2
　>>> [[a, b] for a in range(5) for b in range(a)]
　[[1, 0], [2, 0], [2, 1], [3, 0], [3, 1], [3, 2], [4, 0], [4, 1], [4, 2], [4, 3]]

を得る。

Julia は Python が 0 オリジンなのに対して 1 オリジンなので，以下のようになる。

  [[a, b] for a in 1:5 for b in 1:a-1]

  10-element Vector{Vector{Int64}}:
   [2, 1]
   [3, 1]
   [3, 2]
   [4, 1]
   [4, 2]
   [4, 3]
   [5, 1]
   [5, 2]
   [5, 3]
   [5, 4]

  Python と同じ添え字が必要なら，

  [[a-1, b-1] for a in 1:5 for b in 1:a-1]

  10-element Vector{Vector{Int64}}:
   [1, 0]
   [2, 0]
   [2, 1]
   [3, 0]
   [3, 1]
   [3, 2]
   [4, 0]
   [4, 1]
   [4, 2]
   [4, 3]

意味ねえ〜〜〜〜

列挙順序は異なるが，以下のようにも。

  using Combinatorics
  for i in combinations(1:5, 2)
     println(i)
  end

  [1, 2]
  [1, 3]
  [1, 4]
  [1, 5]
  [2, 3]
  [2, 4]
  [2, 5]
  [3, 4]
  [3, 5]
  [4, 5]

順序を揃えたいなら

  using Combinatorics
  for i in combinations(1:5, 2)
     println([i[2], i[1]])
  end

  [2, 1]
  [3, 1]
  [4, 1]
  [5, 1]
  [3, 2]
  [4, 2]
  [5, 2]
  [4, 3]
  [5, 3]
  [5, 4]

とか

  using Combinatorics
  for i in combinations(1:5, 2)
     println([i[2]-1, i[1]-1])
  end

  [1, 0]
  [2, 0]
  [3, 0]
  [4, 0]
  [2, 1]
  [3, 1]
  [4, 1]
  [3, 2]
  [4, 2]
  [4, 3]

Julia の小ネタ--038 文字列からデータフレームを読み込む

Julia の小ネタ--038 文字列からデータフレームを読み込む

　そのような場合には，プログラム中に「""" 改行を含む文字列 """」のようにデータを記述し，そこからデータフレームに読み込むことができる。
　CSV.read( ) の第1引数は通常はファイルパスであるが，IOBffer( ) で引数に文字列を指定することもできる。
　欄の区切り文字は delim で指定するが，例のように空白で（桁を揃えて）区切られている場合は，ignorerepeated=true を指定しなければならない。

  using CSV, DataFrames
  anscombe = CSV.read(IOBuffer("""
      x1    x2    x3    x4    y1    y2    y3    y4
      10    10    10     8  8.04  9.14  7.46  6.58
       8     8     8     8  6.95  8.14  6.77  5.76
      13    13    13     8  7.58  8.74 12.7   7.71
       9     9     9     8  8.81  8.77  7.11  8.84
      11    11    11     8  8.33  9.26  7.81  8.47
      14    14    14     8  9.96  8.1   8.84  7.04
       6     6     6     8  7.24  6.13  6.08  5.25
       4     4     4    19  4.26  3.1   5.39 12.5
      12    12    12     8 10.8   9.13  8.15  5.56
       7     7     7     8  4.82  7.26  6.42  7.91
       5     5     5     8  5.68  4.74  5.73  6.89
  """), DataFrame, delim=" ", ignorerepeated=true)

11 rows × 8 columns

	x1	x2	x3	x4	y1	y2	y3	y4
	Int64	Int64	Int64	Int64	Float64	Float64	Float64	Float64
1	10	10	10	8	8.04	9.14	7.46	6.58
2	8	8	8	8	6.95	8.14	6.77	5.76
3	13	13	13	8	7.58	8.74	12.7	7.71
4	9	9	9	8	8.81	8.77	7.11	8.84
5	11	11	11	8	8.33	9.26	7.81	8.47
6	14	14	14	8	9.96	8.1	8.84	7.04
7	6	6	6	8	7.24	6.13	6.08	5.25
8	4	4	4	19	4.26	3.1	5.39	12.5
9	12	12	12	8	10.8	9.13	8.15	5.56
10	7	7	7	8	4.82	7.26	6.42	7.91
11	5	5	5	8	5.68	4.74	5.73	6.89

Anscombe データセットの分析

1.　Anscombe データセットの分析

Anscombe データセットは，記述統計学においてときどき言及されるものである。
4 組のデータ (x1, y1), (x2, y2), (x3, y3), (x4, y4) は，それぞれの変数の平均値，分散，二変数間の共分散，したがって相関係数も全て同じというものである。

  #   x1    x2    x3    x4    y1    y2    y3    y4
  data = [
      10    10    10     8  8.04  9.14  7.46  6.58
       8     8     8     8  6.95  8.14  6.77  5.76
      13    13    13     8  7.58  8.74 12.7   7.71
       9     9     9     8  8.81  8.77  7.11  8.84
      11    11    11     8  8.33  9.26  7.81  8.47
      14    14    14     8  9.96  8.1   8.84  7.04
       6     6     6     8  7.24  6.13  6.08  5.25
       4     4     4    19  4.26  3.1   5.39 12.5 
      12    12    12     8 10.8   9.13  8.15  5.56
       7     7     7     8  4.82  7.26  6.42  7.91
       5     5     5     8  5.68  4.74  5.73  6.89
  ];
  using DataFrames
  df = DataFrame(data, [:x1, :x2, :x3, :x4, :y1, :y2, :y3, :y4])
  using Statistics
  [println("mean(x$i) = $(mean(df[:, i])),  mean(y$i) = $(mean(df[:, 4+i]))") for i in 1:4];
  [println("var(x$i) = $(var(df[:, i])),  var(y$i) = $(var(df[:, 4+i]))") for i in 1:4];
  [println("cov(x$i, y$i) = $(cov(df[:, i], df[:, 4+i])),  cor(x$i, y$i) = $(cor(df[:, i], df[:, 4+i]))") for i in 1:4];

  mean(x1) = 9.0,   mean(y1) = 7.497272727272727
  mean(x2) = 9.0,   mean(y2) = 7.500909090909091
  mean(x3) = 9.0,   mean(y3) = 7.496363636363637
  mean(x4) = 9.0,   mean(y4) = 7.50090909090909
  var(x1)  = 11.0,  var(y1)  = 4.100701818181819
  var(x2)  = 11.0,  var(y2)  = 4.127629090909091
  var(x3)  = 11.0,  var(y3)  = 4.080845454545455
  var(x4)  = 11.0,  var(y4)  = 4.12324909090909
  cov(x1, y1) = 5.489,  cor(x1, y1) = 0.8172742068397078
  cov(x2, y2) = 5.5,    cor(x2, y2) = 0.8162365060002429
  cov(x3, y3) = 5.481,  cor(x3, y3) = 0.8180660798450472
  cov(x4, y4) = 5.499,  cor(x4, y4) = 0.8165214368885028

よく使われる統計量で見分けが付かなくても，これらを散布図で見れば，明らかな違いがある(fig1, fig2, fig3, fig4)。図に示した直線は回帰直線である。

  using Plots
  pyplot(grid=false, label="", xlabel="x", ylabel="y")
  plt1 = scatter(df.x1, df.y1, smooth=true, title="fig1");
  plt2 = scatter(df.x2, df.y2, smooth=true, title="fig2");
  plt3 = scatter(df.x3, df.y3, smooth=true, title="fig3");
  plt4 = scatter(df.x4, df.y4, smooth=true, title="fig4");
  plt5 = scatter(df.y4, df.x4, smooth=true, xlabel="y", ylabel="x", title="fig5");
  plot(plt1, plt2, plt3, plt4, plt5)

統計図の重要性を説くためのうってつけのデータセットである。

違いは確かにあるが，その先はどうするのかについてはあまり言及がない。予測という観点からデータを見てみよう。

1.1.　fig2 は曲線相関である（2次曲線）ので，y = a + b x + c x^2 に当てはまる

  using GLM
  df.x_power2 = df.x1 .^ 2
  result2 = lm(@formula(y2 ~ x2 + x_power2), df)

  StatsModels.DataFrameRegressionModel{LinearModel{LmResp{Vector{Float64}}, DensePredChol{Float64, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}}}, Matrix{Float64}}
  
  Formula: y2 ~ 1 + x2 + x_power2
  
  Coefficients:
  ──────────────────────────────────────────────────────
                Estimate   Std.Error   t value  Pr(>|t|)
  ──────────────────────────────────────────────────────
  (Intercept)  -5.99573   0.00432995  -1384.71    <1e-22
  x2            2.78084   0.00104006   2673.74    <1e-24
  x_power2     -0.126713  5.70977e-5  -2219.24    <1e-23
  ──────────────────────────────────────────────────────

予測値は完全に当てはまる。

  scatter(df.x2, df.y2)
  o = sortperm(df.x2)
  xval = minimum(df.x2):0.05:maximum(df.x2)
  predict2 = coef(result2)[1] .+ coef(result2)[2] .* xval + coef(result2)[3] .* xval .^2
  plot!(xval, predict2)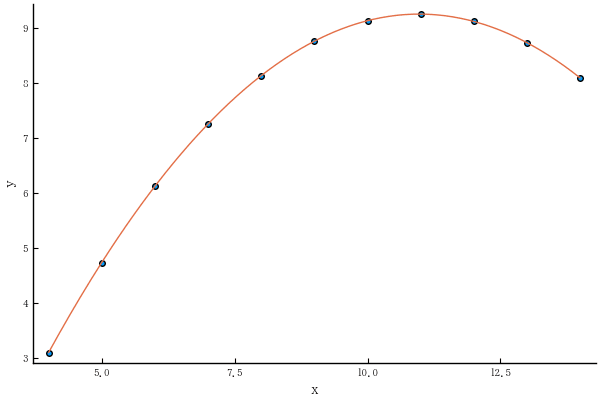

1.2.　fig3 は，特異値があるので，ダミー変数を用いて当てはめができる

  df.x3_dummy = df.x3 .== 13
  result3 = lm(@formula(y3 ~ x3 + x3_dummy), df)

  StatsModels.DataFrameRegressionModel{LinearModel{LmResp{Vector{Float64}}, DensePredChol{Float64, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}}}, Matrix{Float64}}
  
  Formula: y3 ~ 1 + x3 + x3_dummy
  
  Coefficients:
  ─────────────────────────────────────────────────────
               Estimate    Std.Error  t value  Pr(>|t|)
  ─────────────────────────────────────────────────────
  (Intercept)   4.00565  0.00292424   1369.81    <1e-22
  x3            0.34539  0.000320591  1077.35    <1e-21
  x3_dummy      4.20429  0.0035265    1192.2     <1e-21
  ─────────────────────────────────────────────────────

予測値は完全に当てはまる。

  scatter(df.x3, df.y3)
  o = sortperm(df.x3)
  plot!(df.x3[o], predict(result3)[o])

1.3.　fig4 は座標軸を入れ替えて，非線形関数に当てはめる

fig4 の x座標，y座標を入れ替えたものが fig5 である。回帰直線に当てはめるとどちらも同じようであるが，fig5 にロジスティック曲線を当てはめてみよう。
すなわち，図（データ）の解釈として，「従属変数 x は二値データ。独立変数 y が小さい内は反応がない（x=8)が，yが大きくなると反応が現れる（x = 19)」と考える。
なお，このままだと当てはめができないので，一点だけ変更する（下図の上に2点ある左の方）。

  df.x4p = df.y4 .> 10
  df.x4p[5] = 1
  result4 = glm(@formula(x4p ~ y4), df, Binomial())

  StatsModels.DataFrameRegressionModel{GeneralizedLinearModel{GlmResp{Vector{Float64}, Binomial{Float64}, LogitLink}, DensePredChol{Float64, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}}}, Matrix{Float64}}
  
  Formula: x4p ~ 1 + y4
  
  Coefficients:
  ─────────────────────────────────────────────────────
                Estimate  Std.Error   z value  Pr(>|z|)
  ─────────────────────────────────────────────────────
  (Intercept)  -19.574     18.437    -1.06167    0.2884
  y4             2.20803    2.20089   1.00324    0.3157
  ─────────────────────────────────────────────────────

予測曲線を描いてみるともっともらしく見えるようになる。

  scatter(df.y4, df.x4p)
  xval = minimum(df.y4):0.05:maximum(df.y4)
  predict4 = 1 ./ (1 .+ exp.(-coef(result4)[1] .- coef(result4)[2] .* xval))
  plot!(xval, predict4)

2.　まとめ

以上のように，データの姿形，理論的背景をよく考えてモデルを構築する必要があるということだ。

Julia で，for ループの大域脱出法

1.　for ループの大域脱出法

多重 for ループの最も内側から一挙に最も外側の for ループのさらに外へ脱出する方法を何通りか記述する。

1.1.　状況を表す変数を使う方法

• 一番外側の for ループに入る前に success = false としておく。
• もっとも内側の for ループから脱出するときに，success = true として break で脱出する。
• 脱出した for ループで success の値をチェックし true ならばさらに break する。

これを繰り返して，一番外側の for ループも脱出する。
脱出開始時と脱出完了時の変数の値をみれば，確かに大域脱出していることが確認できる。
なお，success && break は
　if success
　　　break
　end
と同じである。

  success = false
  count = 0
  for i1 in 1:10
  for i2 in 1:10
          for i3 in 1:10
              for i4 in 1:10
                  count += 1
                  if i1 == 2 && i2 == 3 && i3 == 4 && i4 == 5
                      success = true
                      println("最も内側から break するときの状態　success = $success, count = $count")
                      break
                  end
                  success && break
              end
              success && break
          end
          success && break
  end
  success && break
  end
  println("脱出後の状態　success = $success, count = $count")

  最も内側から break するときの状態　success = true, count = 1235
  脱出後の状態　success = true, count = 1235

1.2.　関数化する方法

当該処理を関数化しておけば，最も内側の for ループで return を使えば，大域脱出することになる。
最も内側の for ループ中に確実に return するならば，最も外側の for ループの外に何があっても実行されない。

  function f()
  count = 0
  for i1 in 1:10
          for i2 in 1:10
              for i3 in 1:10
                  for i4 in 1:10
                      count += 1
                      if i1 == 2 && i2 == 3 && i3 == 4 && i4 == 5
                          println("最も内側から return するときの状態　count = $count")
                          return
                      end
                  end
              end
          end
  end
  println("この println() は実行されない")
  end
  f()

  最も内側から return するときの状態　count = 1235

1.3.　Julia 独自の for ループ記法を使う方法

Julia では，多重 for ループを一行（for 文 1 個）で書く便法がある。これを使えば，見かけは一重の for ループのようであり，その中で break すれば，最も外側の for ループの外まで一挙に脱出することになる。

  count = 0
  for i1 in 1:10, i2 in 1:10, i3 in 1:10, i4 in 1:10
  count += 1
  if i1 == 2 && i2 == 3 && i3 == 4 && i4 == 5
          println("最も内側から return するときの状態　count = $count")
          break
  end
  end
  println("脱出後の状態　count = $count")

  最も内側から return するときの状態　count = 1235
  脱出後の状態　count = 1235

M1 チップ用 Python 10.0

いまだに pip install scipy できない...

なんという失態

M1 チップ対応の R 4.1.1 と Julia 1.7.0 の速度比較

R すなわち以下の仕様では

R version 4.1.1 Patched (2021-09-05 r80862)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Big Sur 11.6

system.time({
    library(gmp)
    func <- function(n) {
        x <- (n+1):(2*n)
        y <- n*x/(x-n)
        count <- sum(floor(y) == y)
        return(count)
    }
    n <- 2
    while (n <= 180190) {
        if (func(n) > 1000) {
            print(n)
            break
        }
        n <- n+1
    }
})

[1] 180180
   user  system elapsed 
121.496  32.980 154.516 

#####

Julia 1.6.3 M1 チップ非対応では，

function func(n)
    x = (n+1):(2*n)
    y = n .*x ./ (x .- n)
    sum(floor.(Int, y) .== y)
end

function f()
    n = 2
    while n <= 180190
       if func(n) > 1000
          println(n)
          break
       end
       n += 1
    end
end

@time f()
# 180180
#  68.376876 seconds (947.74 k allocations: 123.598 GiB, 2.28% gc time)

まあ，2倍くらい速い。

#####

Julia 1.7.0 M1 チップ対応ではあるが開発途上，ではさらに速い

@time f()
# 180180
#  39.769370 seconds (971.07 k allocations: 123.592 GiB, 9.96% gc time, 0.03% compilation time)

#####

ちなみに，Python 3.10 でもやってみようと思ったが，動かし方を忘れてしまった。

M1 チップの場合は，専用の R をインストールしよう

R のインストールは

https://cran.ism.ac.jp/bin/macosx/

からやっていると思うけど，M1 チップ用の R は，下の方に

big-sur-arm64

Binaries for macOS 11 or higher (Big Sur) for arm64-based Macs (aka Apple silicon such as the M1 chip)

https://cran.ism.ac.jp/bin/macosx/big-sur-arm64/

というのがあるからね！！！

 

M1 チップに対応しているアプリを使おう（Mac）

9 年間使ってきた MacBook であるが，夏場になると CPU の放熱が追いつかず kernelpanic になってしまうなど不都合が目立ってきたので，M1 チップ搭載の Mac Mini を導入した。

R を起動しようとしたとき，不気味なメッセージが出たのだった。「"App" を開くには，Rosetta をインストールする必要があります」。Intel CPU のためのアプリが M1 で動くようにするためのものだそうで。

不安は的中で，Mac Book での実行時間が 40 秒ほどのプログラムが，Mac mini だと 50 秒ほどかかる。購入したのは失敗だったか... と思うのはまだ早い。

ずいぶん前から，https://mac.r-project.org/ で big-sur/arm64 用の R がリリースされている。

これをインストールして同じプログラムを実行すると 18 秒だった。2 倍速い。

M1 チップに純正対応しているアプリはまだ少ないようだが，これからが楽しみだ。

2021/10/22 現在，

M1 チップ対応　　Python 3.10　（3.8 では非対応，3.9 は知らない）

M1 チップ非対応 　Julia 1.6.3　　（1.7.0 で対応予定）

「サンタクロースはいない」ことはない

https://nazesuugaku.com/santaclausinai/

> サンタクロースがいないことを証明するために、サンタクロースの条件を定義したいと思います。

> サンタクロースは世界に1人しかいない

この条件は誰もが認めるものではない（誰も証明できない，あるいはその反証がないならな）ので，前提条件が否定されれば，当然のことながらあとは，全てなりたちません。

全世界のよい子たち，サンタクロースはいますよ。

＝＝＝＝＝

サンタクロースがいないことを証明してやるよwww
https://sekayume.com/?p=2456

サンタがいないことを物理的に証明する動画
https://www.youtube.com/watch?v=-uTGB-D0PQ4

世の中には，ヒドイ人間がある程度はいますね。

Julia で，クロンバックの α の検定と推定

1.　クロンバックの α の検定と推定

https://www.real-statistics.com/reliability/internal-consistency-reliability/cronbachs-alpha/cronbachs-alpha-continued/
Cronbach’s Alpha Hypothesis Testing

1.1.　仮説検定

帰無仮説が γ < γ0 のときは F 分布の下側確率，γ > γ0 のときは F 分布の上側確率を p 値とする。

1.2.　計算例

  n = 15
  k = 10
  γ = 0.591719
  γ0 = 0.7
  W = (1 - γ0) / (1 - γ)

  0.734788050386866

  df1 = n - 1

  14

  df2 = (n - 1) * (k - 1)

  126

  using Rmath
  p = pf(W, df1, df2) # 下側確率

  0.2639546322196921

  using Plots
  plot(x -> df(x, df1, df2), xlims=(0, 3), xlabel="W",
       ylabel="probability density", label="")
  savefig("fig.png")

1 - α の両側信頼区間は以下の式 γL，γU によって求められる。

  α = 0.05 # すなわち 95% 信頼区間を求める

  0.05

  γL = 1 - (1 - γ) * qf(1 - α/2, n - 1, (n - 1) * (k - 1))

  0.19492168920552821

  γU = 1 - (1 - γ) * qf(α/2, n - 1, (n - 1) * (k - 1))

  0.8398208740258171

左片側信頼区間は (γLL, 1)

  γLL = 1 - (1 - γ) * qf(1 - α, n - 1, (n - 1) * (k - 1))

  0.2769247403837999

右片側信頼区間は (-1, γUR)

  γUR = 1 - (1 - γ) * qf(α, n - 1, (n - 1) * (k - 1))

  0.8123375621254263

グレートスローを五連続って！

以前，ポケモンGO! でグレートスローを三連続するまでに何回投げればよいのか？というのを書いたが，最近，「グレートスローを五連続」というタスクが出てきた。

これは実質不可能なタスクだろう。

シミュレーションしてみた。
この場合の if 文の (  ) は必要。

function quintuple(p=0.3)
    count = 0
    while true
        if (count += 1; rand(1)[1] < p)
            if (count += 1; rand(1)[1] < p)
                if (count += 1; rand(1)[1] < p)
                    if (count += 1; rand(1)[1] < p)
                        if (count += 1; rand(1)[1] < p)
                            return count
                        end
                    end
                end
            end
        end
    end
end

using Plots
x = Int[]
for i in 1:100000
    count = quintuple(0.3)
    append!(x, count)
end
mean(x)
median(x)
histogram(x)

グレートスローを投る確率 p が 0.3 のときでも，平均で600回近く，メディアンでも400回ほど。

確率が 0.1 なんてときには，平均で10万回投げないと達成できない。

以下の図は p = 0.3 のときの達成までの回数のヒストグラム

 

見かけの長精度表示

大変よくできたネタだったのに，投稿主さんが消してしまったので，再現しておく。

Python では，整数は自動的に長精度になるので，もしかしたら正しいのかなと眉に唾して読んだ。

ans = 545783032743912028389476341548725567488.0
print(ans)        # 5.45783032743912e+38 完全な桁を書きたい
intAns = int(ans) # こうすればいい
print(intAns)     # 545783032743912028389476341548725567488

そんなことないだろうと，調べてみた。

545783032743912028389476341548725567488 はかなり特殊な数，
hex(545783032743912028389476341548725567488)
= '0x19a99fd143bee50000000000000000000' のように下位桁が0で,0x19a99fd143bee5 = 7223378293538533 は16桁で64ビット実数でかろうじて表せる整数。

ans の先頭 15 桁とその後に 0，最後に 1 でも，このようなことは成り立たないことがわかる。

ans1 = 545783032743912000000000000000000000001.0
print(ans1)       # 5.45783032743912e+38
intAns1 = int(ans1)
print(intAns1)    # 545783032743912028389476341548725567488

Julia なら，BigInt, BigFloat, big"数値を表す文字列" を使う。

b = 545783032743912000000000000000000000001.0
print(b)          # 5.45783032743912e38
print(BigInt(b))  #  545783032743912028389476341548725567488
b = big"545783032743912000000000000000000000001.0" # 文字列で与える
print(b)          # 5.45783032743912000000000000000000000001e+38
print(BigInt(b))  #  545783032743912000000000000000000000001

for ループ（ジェネレータ式）を使うか使わないか，それが問題だ！！

ジェネレータ式（内包表記）で書かれたプログラムがあったのだけど，説明はあるものの，読んだだけでは何をするプログラムかちょっとわかりにくかった。
Julia では，「ベクトル化関数をつかうよりむしろループを書け」という人もいるようなのだけど，ちょっと確かめてみようと思った次第である。

1.　紹介されていたプログラム

プログラム中の numerator は上式の分子，すなわち a の各項の指数をとったもの，sum_exp_a はその総和，最後に y は numerator の各項を sum_exp_a で割ったものを返すということで，素直といえば素直なのだけど，ループをジェネレータ式で書いているということ。 その割には，総和は reduce で計算したりしている（reduce は　for ループで書いてもほとんど同じパフォーマンスであった）。

  function func(a)
      len_a = length(a)                               # S01
      numerator = [exp(a[i]) for i=1:len_a]           # S02
      sum_exp_a = reduce(+, numerator)                # S03
      y = [numerator[i] / sum_exp_a for i=1:len_a]    # S04
      return y
  end

  func (generic function with 1 method)

2.　実行速度を計測する

第一引数は実行速度を計算される関数の名前である。

  function test(FUNC, a, n=100)
      for i = 1:n
          FUNC(a)
      end
  end

  test (generic function with 2 methods)

2.1.　ジェネレータ式を使って書かれたプログラム

  a = randn(10000000);
  @time test(func, a)

   14.059123 seconds (163.74 k allocations: 14.910 GiB, 3.66% gc time, 0.63% compilation time)

2.2.　ベクトル化した関数を使って書かれたプログラム

sum_exp_a は sum() で求め，numerator の各項を ./ で割り算する。
関数が何をしているかは，Julia プログラムになれているとすぐに理解できる。

  function func2(a)
      numerator = exp.(a)            # S02
      numerator ./ sum(numerator)    # S04
  end
  
  @time test(func2, a)

   12.133699 seconds (32.60 k allocations: 14.903 GiB, 4.31% gc time, 0.37% compilation time)

2.3.　for ループを使って書かれたプログラム

  function func3(a)
      numerator = similar(a)
      len_a = length(a)                # S01
      sum_exp_a = 0
      for i = 1:len_a
          numerator[i] = exp(a[i])     # S02
          sum_exp_a += numerator[i]    # S03
      end
      for i = 1:len_a
          numerator[i] /= sum_exp_a    # S04
      end
      numerator
  end
  
  @time test(func3, a)

   15.028953 seconds (23.41 k allocations: 7.452 GiB, 1.82% gc time, 0.16% compilation time)

2.4.　for ループを使って書かれたプログラム　その 2

  function func4!(a)
      len_a = length(a)        # S01
      sum_exp_a = 0
      for i = 1:len_a
          a[i] = exp(a[i])     # S02
          sum_exp_a += a[i]    # S03
      end
      for i = 1:len_a
          a[i] /= sum_exp_a    # S04
      end
  end
  
  @time test(func4!, a)

   14.219583 seconds (22.84 k allocations: 1.357 MiB, 0.16% compilation time)

3.　実行速度のまとめ

• 一番早いのは，関数（ベクトル化した関数）を使うプログラムである。ジェネレータ式を使って書かれたプログラムより 1.1 倍ほど速い。プログラムが，何をやっているかもすぐわかるし，短いし。
• for ループを使って書かれたプログラムはジェネレータ式を使ったプログラムとほぼ同じである（ジェネレータ式は結局は for ループと同じなので当たり前といえば当たり前。いずれも，わかりにくい！！！

結論：いつでもそうではないかも知れないが，関数（ベクトル化した関数）を使うべし？かな？？？

4.　最後に

アルゴリズム，計算順序の違いで，誤差範囲の違いは生じる。
まあ，計算誤差の範囲内で，どの関数も同じ結果を返すということがわかった。

  a = randn(10000000)
  result = func(a)
  result2 = func2(a)
  result3 = func3(a)
  x = copy(a)
  func4!(x)
  println(all(abs.(result .- result2) .< eps()))
  println(all(abs.(result .- result3) .< eps()))
  println(all(abs.(result .- x) .< eps()))

  true
  true
  true

  println(eps())

  2.220446049250313e-16

Julia バージョンアップ v1.6.3 (2021/09/23)

https://julialang.org/downloads/

Current stable release: v1.6.3 (Sep 23, 2021)

Julia で「クロンバックの α」

クロンバックの α，標準化されたクロンバックの α，Kuder-Richardson の方法についても述べる。

1.　クロンバックの α

順序尺度変数やリッカート法により得られる回答データにも対応しているので，後述する "Kuder-Richardson の式 20" より優れている。

1.1.　定義

• k：質問項目数
• x_j：質問_j への回答
• t：回答の合計 t = sum(x)
• cov(x_i, x_j)：質問_i への回答と質問_j への回答の不偏共分散
• var(x_i), var(t)：質問_iへの回答，回答の合計の不偏分散

https://www.real-statistics.com/reliability/internal-consistency-reliability/cronbachs-alpha/cronbachs-alpha-basic-concepts/
Cronbach’s Alpha Basic Concepts

1.2.　計算例

  data = [1 1 1 1 1 1 1 1 1 1 1
          1 1 1 1 1 1 1 1 0 1 0
          1 0 1 1 1 1 1 1 1 0 0
          1 1 1 0 1 1 0 1 1 0 0
          1 1 1 1 1 0 0 0 1 0 0
          0 1 1 0 1 1 1 1 0 0 0
          1 1 1 1 0 0 1 0 0 0 0
          1 1 1 1 1 0 0 0 0 0 0
          0 1 0 1 1 0 0 0 0 1 0
          1 0 0 1 0 1 0 0 0 0 0
          1 1 1 0 0 0 0 0 0 0 0
          1 0 0 1 0 0 0 0 0 0 0];

  k = size(data, 2)

  11

  t = sum(data, dims=2)

  12×1 Matrix{Int64}:
   11
    9
    8
    7
    6
    6
    5
    5
    4
    3
    3
    2

  varx = var(data, dims=1) # 不偏分散でも分散でも，以下と統一していればどちらでも可

  1×11 Matrix{Float64}:
   0.151515  0.204545  0.204545  0.204545  …  0.242424  0.204545  0.0833333

  Σvarx = sum(varx)

  2.3409090909090913

  vart = var(t) # 不偏分散でも分散でも，上と統一していればどちらでも可

  7.113636363636363

  α = k / (k-1) * (1 - Σvarx / vart)

  0.7380191693290735

1.3.　Julia の関数として定義

  using LinearAlgebra, Statistics
  function alpha0(x)
      k = size(x, 2)
      VarCovMat = cov(x)
      Sy2 = sum(VarCovMat)
      Sj2 = sum(diag(VarCovMat))
      k / (k - 1) * (1 - Sj2 / Sy2)
  end

  alpha0 (generic function with 1 method)

上式の 2 番目の式を関数化する。

  using Statistics
  function alpha(x)
      k = size(x, 2)
      varx = var(x, dims=1)
      y = sum(x, dims=2)
      k / (k - 1) * (1 - sum(varx) / var(y))
  end

  alpha (generic function with 1 method)

1.4.　計算例

  alpha0(data)

  0.7380191693290735

  alpha(data)

  0.7380191693290735

以下のデータは 3 件法での回答を求めたものである。

  data2 = [1 1 1
           2 1 1
           2 1 2
           3 2 1
           2 3 2
           2 3 3
           3 2 3
           3 3 3
           2 3 2
           3 3 3];

  alpha0(data2)

  0.7734375

  alpha(data2)

  0.7734375000000003

ちなみに，R では，psych::alpha で計算できる。

  using RCall
  R"""
  library(psych)
  results = alpha($(data2))
  options(digits=16)
  print(results$total$raw_alpha)
  """;

  [1] 0.7734375

なお，psych::alpha( ) は相関係数を与えるオプションもあるが，粗データを与えた場合と結果が違う。

  using RCall
  R"""
  library(psych)
  results2 = alpha(cor($(data2)))
  options(digits=16)
  print(results2$total$raw_alpha)
  """;

  [1] 0.7742910373931703

オンラインヘルプを見ると，

When calculated from the item variances and total test variance, as is done here, raw alpha is sensitive to differences in the item variances. Standardized alpha is based upon the correlations rather than the covariances.

というくだりがある。つまり，変数（質問への回答）を標準化する方がよいとのことである。そこで，元データを標準化して alpha( ) に与えてやると確かに同じ値になる。

  using RCall
  R"""
  library(psych)
  scaled = scale($(data2))
  results2 = alpha(scaled)
  options(digits=16)
  print(results2$total$raw_alpha)
  """;

  [1] 0.7742910373931704

1.5.　相関係数を与えて標準化されたクロンバックの α を求める

https://towardsdatascience.com/cronbachs-alpha-theory-and-application-in-python-d2915dd63586
Cronbach’s Alpha: Theory and Application in Python

1.6.　定義

• k：質問項目数
• r：質問項目間の相関係数の平均値（相関係数行列の対角要素を含まない上三角行列の相関係数 r(i, j), i < j の平均値）

注意：元の Web ページのどこにも書いていないが，α_st と記述されている点に注意。つまり「標準化されたクロンバックのα）の意なのだ。

Web ページには Python での関数が示されている。

  def cronbach_alpha(df):
      # 1. Transform the df into a correlation matrix
      df_corr = df.corr()

      # 2.1 Calculate N
      # The number of variables equals the number of columns in the df
      N = df.shape[1]

      # 2.2 Calculate R
      # For this, we'll loop through the columns and append every
      # relevant correlation to an array calles "r_s". Then, we'll
      # calculate the mean of "r_s"
      rs = np.array([])
      for i, col in enumerate(df_corr.columns):
          sum_ = df_corr[col][i+1:].values
          rs = np.append(sum_, rs)
      mean_r = np.mean(rs)

      # 3. Use the formula to calculate Cronbach's Alpha 
      cronbach_alpha = (N * mean_r) / (1 + (N - 1) * mean_r)
      return cronbach_alpha

これを Julia に書き換える。

  using Statistics
  
  function cronbach_alpha(df)
      # 1. Transform the df into a correlation matrix
      r = cor(df)
  
      # 2.1 Calculate N
      # The number of variables equals the number of columns in the df
      N = size(df, 2)
  
      # 2.2 Calculate R
      # For this, we'll loop through the columns and append every
      # relevant correlation to an array calles "r_s". Then, we'll
      # calculate the mean of "r_s"
      r_s = []
      for i = 1:N-1
          for j = i+1:N
              append!(r_s, r[i, j])
          end
      end
      mean_r = mean(r_s)
  
      # 3. Use the formula to calculate Cronbach's Alpha 
      (N * mean_r) / (1 + (N - 1) * mean_r)
  end

  cronbach_alpha (generic function with 1 method)

  cronbach_alpha(data2)

  0.7742910373931706

確かに，psych::alpha( ) の結果と一致した。

標準化というのは全ての変数の分散を同じにする（全ての変数を同格に扱う）ということである。
普通にクロンバックの α が使われる状況は，質問項目の回答の分散が大きく変わることはない（ほとんどの質問項目は 5 件法，ある項目は 0 ~ 100 の満足度などというのはあり得ない）。
なので，標準化されたクロンバックの α も，通常のクロンバックの α もほとんど同じ値になるだろう。
クロンバックの α の応用法として，ある質問項目を除いたら α がどれぐらい変化するかを検討することがある。この場合に使うのは標準化されないクロンバックの α である。

ということで，伝統的な（標準化しない）クロンバックの α を使う方がよいだろう。

2.　Kuder and Richardson Formula 20

質問項目への回答が二値データ（たとえば 0/1）の場合には，"Kuder-Richardson の式 20"  を適用することができ，クロンバックの α と全く同じ結果が得られる。

2.1.　定義

• k：質問項目数
• p_j：質問_j に正解であった回答者数
• q_j：質問_j に不正解であった回答者数
• σ²：回答者ごとの得点（正解数）の分散（不偏分散ではない）

ρ_KR20 は 0 ~ 1 の範囲の値をとり，値が大きいことは信頼性があることを示す。しかし，あまりにも大きい数値（たとえば 0.9 以上）の場合は，質問紙が均質である（悪い意味で「それぞれの質問はほとんど同じ」）ことを示す。

https://www.real-statistics.com/reliability/internal-consistency-reliability/kuder-richardson-formula-20/
Kuder and Richardson Formula 20

2.2.　計算例

  n, k = size(data)

  (12, 11)

  p = sum(data, dims=1) ./ n

  1×11 Matrix{Float64}:
   0.833333  0.75  0.75  0.75  0.666667  …  0.416667  0.333333  0.25  0.0833333

  q = 1 .- p

  1×11 Matrix{Float64}:
   0.166667  0.25  0.25  0.25  0.333333  …  0.583333  0.666667  0.75  0.916667

  pq = p .* q

  1×11 Matrix{Float64}:
   0.138889  0.1875  0.1875  0.1875  0.222222  …  0.222222  0.1875  0.0763889

  Σpq = sum(pq)

  2.1458333333333335

  using Statistics
  σ² = var(totalscores, corrected=false) # 注：不偏分散ではない

  6.520833333333333

  ρKR20 = (1 - Σpq / σ²) * k / (k - 1)

  0.7380191693290734

2.3.　Julia の関数として定義

  using Statistics
  
  function KR20(x)
  n, k = size(x)
  p = sum(data, dims=1) ./ n
  q = 1 .- p
  pq = p .* q
  Σpq = sum(pq)
  σ² = var(totalscores, corrected=false)
  (1 - Σpq / σ²) * k / (k - 1)
  end

  KR20 (generic function with 1 method)

前節の計算例のような 0/1 回答のデータに対して計算される "Kuder-Richardson の式 20" は，クロンバックの α と全く同じである。

  alpha0(data)

  0.7380191693290735

  alpha(data)

  0.7380191693290735

  KR20(data)

  0.7380191693290734