素数の日付を含む最長期間
締め切りが 2017/05/30 10:00 AM なので,その 1 分後に投稿されるように予約
設問
日付をYYYYMMDD形式で表現し、8桁の数値としてみたとき、その値が素数かどうかを判定します。
1970年1月1日~2019年12月31日までの50年間のうち、素数がちょうど n 個含まれる期間で最長のものを考え、その日数を求めます。
なお、日数は両端の日付を含んで数えるものとします。
また、閏年は考慮するものとします。
例えば、n = 3 のとき、以下の青色で塗りつぶした範囲が最長になり、その日数は「202」です。

2015-04-11 : 素数
2015-04-12 : 開始日
2015-05-13 : 素数
2015-08-21 : 素数
2015-10-11 : 素数
2015-10-30 : 終了日
2015-10-31 : 素数
標準入力から n が与えられたとき、その最長日数を求め、標準出力に出力してください。
なお、n は1000以下の自然数とします。
【入出力サンプル】
標準入力
3
標準出力
202
-------------------------------------
R で書くと実行時間が1秒以内に収まらない
is.prime = function(n) {
if (n %% 2 == 0) return(FALSE)
else if(n %% 3 == 0) return(FALSE)
maxitr = as.integer(sqrt(n))
i = 1
repeat {
i = i+4
if (i > maxitr) return(TRUE)
else if (n %% i == 0) return(n == i)
i = i+2
if (i > maxitr) return(TRUE)
else if (n %% i == 0) return(n == i)
}
}
J.day = function(iy, jm, kd) {
tmp = -(jm < 3)
kd - 32075 + (1461 * (iy + 4800 + tmp))%/%4 + (367 * (jm - 2 - tmp * 12))%/%12 - (3 * ((iy + 4900 + tmp)%/%100))%/%4
}
date2 = function(jul) {
l = jul + 68569
n = (4 * l)%/%146097
l = l - (146097 * n + 3)%/%4
iy = (4000 * (l + 1))%/%1461001
l = l - (1461 * iy)%/%4 + 31
jm = (80 * l)%/%2447
kd = l - (2447 * jm)%/%80
l = jm%/%11
jm = jm + 2 - 12 * l
iy = 100 * (n - 49) + iy + l
iy*10000+jm*100+kd
}
f = function(n) {
begin = J.day(1970, 1, 1)
end = J.day(2019, 12, 31)
count = 0
p.date = integer(1100)
for (i in begin:end) {
date = date2(i)
if (is.prime(date)) {
count = count+1
p.date[count] = i
}
}
Max = 0
for (i in 1:(count-n-1)) {
Max = max(Max, p.date[i+n+1]-p.date[i]-1)
}
cat(Max)
}
# f(scan(file("stdin", "r")))
# f(3) # 202
# f(10) # 413
# f(333) # 5771
# f(876) # 14708
# f(999) # 16724
awk で書いて少し速くなって,パスした
function isPrime(n, maxitr, i) {
if (n % 2 == 0) return 0
else if(n % 3 == 0) return 0
maxitr = int(sqrt(n))
i = 1
for (;;) {
i = i+4
if (i > maxitr) return 1
else if (n % i == 0) return n == i
i = i+2
if (i > maxitr) return 1
else if (n % i == 0) return n == i
}
}
function Jday(iy, jm, kd, tmp) {
tmp = -(3 > jm)
return kd - 32075 + int((1461 * (iy + 4800 + tmp))/4) + int((367 * (jm - 2 - tmp * 12))/12) - int((3 * (int((iy + 4900 + tmp)/100)))/4)
}
function revJday(jul, l, n, iy, jm, kd) {
l = jul + 68569
n = int((4 * l)/146097)
l = l - int((146097 * n + 3)/4)
iy = int((4000 * (l + 1))/1461001)
l = l - int((1461 * iy)/4) + 31
jm = int((80 * l)/2447)
kd = l - int((2447 * jm)/80)
l = int(jm/11)
jm = jm + 2 - 12 * l
iy = 100 * (n - 49) + iy + l
return iy*10000+jm*100+kd
}
function max(x, y) {
return x >= y ? x : y
}
function f(n, i, begin, end, count, primeDate, date, Max) {
begin = Jday(1970, 1, 1)
end = Jday(2019, 12, 31)
count = 0
for (i = begin; end >= i; i++) {
date = revJday(i)
if (isPrime(date)) {
primeDate[++count] = i
}
}
Max = 0
for (i = 1; count-n-1 >= i; i++) {
Max = max(Max, primeDate[i+n+1]-primeDate[i]-1)
}
print Max
}
BEGIN {
f(3)
f(10)
f(333)
f(876)
f(999)
}
異なる整数で作る逆三角形
締め切りが 2017/05/23 10:00 AM なので,その 1 分後に投稿されるように予約
設問
n 個の自然数を1段目に並べます。
2段目は n-1 個の自然数を、3段目は n-2 個の自然数を、…というように、図のように逆三角形の形に並べます。
このとき、2段目以降の自然数はそれぞれ、その自然数の左上と右上の数の和とします。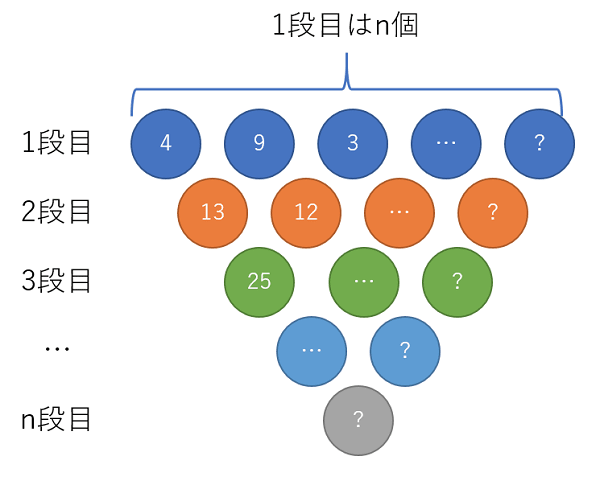
n 段目までに登場するすべての数が重複しないように1段目の数を選んだ時、n 段目の数が最小になるものを求めます。
ただし、いずれの数も正の整数とします。
例えば、n = 3 のとき、以下の左のようにすると3が重複しています。
そこで、右のように配置すると重複はなく、3段目が最小である「8」となります。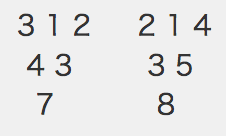
標準入力から n が与えられたとき、標準出力に n 段目の値を出力してください。
なお、n は 1≦n≦7を満たす整数とします。
【入出力サンプル】
標準入力
3
標準出力
8
===================================
R で,簡単に書ける。が,n = 7 のときは 6 秒ほどかかるので,後で Java で書き換える。
F = function(n) {
G = function(X) {
for (k in 1:nrow(p)) {
x = X[p[k,]]
if (sum(x * weight) >= Min) {
next
}
a[1, ] = x
for (i in 2:n) {
for (j in 1:(n-i+1)) {
a[i, j] = a[i - 1, j] + a[i - 1, j+1]
}
}
result = a[n, 1]
if (result < Min && length(unique(a[a!=0])) == elements) {
Min = result
}
}
Min
}
elements = n*(n+1)/2
Min = 1e10
library(e1071)
p = permutations(n)
a = matrix(0, n, n)
x = combn(13, n)
x = x[, x[1,] == 1]
x = x[, x[2,] == 2]
weight = choose(n-1, 0:(n-1))
for (i in 1:ncol(x)) {
Min = min(Min, G(x[,i]))
}
cat(Min)
}
> system.time(F(3)) # 8
8 ユーザ システム 経過
0.043 0.002 0.045
> system.time(F(4)) # 20
20 ユーザ システム 経過
0.004 0.000 0.003
> system.time(F(5)) # 43
43 ユーザ システム 経過
0.066 0.003 0.068
> system.time(F(6)) # 98, 0.961 seq.
98 ユーザ システム 経過
0.524 0.007 0.521
> system.time(F(7)) # 212, 6.095 sec.
212 ユーザ システム 経過
5.822 0.052 5.850
計算処理時間対策のため,Java に移植。
あっという間に計算が終わる。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
String line;
line = cin.nextLine();
int n = Integer.parseInt(line);
System.out.println(F(n));
}
static int G(int Min, int n, int [] weight, int [] X, int [][] p) {
int i, j, k;
int result;
int [] x = new int[n+1];
int nrow = p.length;
int [][] a = new int[n+1][n+1];
int [] check = new int[n*(n+1)/2];
int m;
boolean dup;
for (k = 1; k < nrow; k++) {
int sum = 0;
for (j = 1; n >= j; j++) {
x[j] = X[p[k][j]];
sum += x[j]*weight[j];
}
if (sum >= Min) continue;
for (j = 1; n >= j; j++) {
a[1][j] = x[j];
}
for (i = 2; n >= i; i++) {
for (j = 1; n-i+1 >= j; j++) {
a[i][j] = a[i-1][j]+a[i-1][j+1];
}
}
result = a[n][1];
m = 0;
for (i = 1; n >= i; i++) {
for (j = 1; n-i+1 >= j; j++) {
check[m++] = a[i][j];
}
}
dup = false;
for (i = 0; i < check.length-1; i++) {
for (j = i+1; j < check.length; j++) {
if (check[i] == check[j]) {
dup = true;
break;
}
}
if (dup == true) break;
}
if (dup == false) {
Min = result;
}
}
return Min;
}
static int F(int n) {
int elements = n * (n + 1) / 2;
int [] weight = new int[n+2];
int Min = 1000000000;
int MAX = 15; // 実際には MAX = 13 で O.K.
int [][] p = permutations(n);
int [] vec = new int[MAX+1];
int [] y = new int[n+1];
int i, j;
for (i = 1; MAX >= i; i++) {
vec[i] = i;
}
for (i = 1; n >= i; i++) {
weight[i] = (int) (factorial(n-1) / factorial(i-1) / factorial(n-i));
}
int [][] x = combn(vec, MAX, n);
int cols = (int) (factorial(MAX) / factorial(n) / factorial(MAX-n));
for (i = 1; cols >= i; i++) {
for (j = 1; n >= j; j++) {
y[j] = x[j][i];
}
Min = Math.min(Min, G(Min, n, weight, y, p));
}
return Min;
}
static double factorial(int n) {
int i;
double result = 1;
for (i = 1; n >= i; i++) {
result *= i;
}
return result;
}
static int[][] permutations(int n) {
int sizeZ = (int)factorial(n);
int sizeX = sizeZ / (n - 1);
int[][] z = new int[sizeZ + 1][n + 1];
int[][] x = new int[sizeX + 1][n + 1];
int nrowZ, ncolZ, nrowX, ncolX;
int i, i2, j, j2;
z[1][1] = 1;
nrowZ = ncolZ = 1;
for (i = 2; n >= i; i++) {
for (i2 = 1; nrowZ >= i2; i2++) {
for (j2 = 1; ncolZ >= j2; j2++) {
x[i2][j2] = z[i2][j2];
}
x[i2][ncolZ + 1] = i;
}
nrowX = nrowZ;
ncolX = ncolZ + 1;
for (j = 1; i >= j; j++) {
for (j2 = 1; nrowX >= j2; j2++) {
for (i2 = 1; ncolX >= i2; i2++) {
z[(j - 1) * nrowX + j2][i2] = x[j2][(j + i2 - 2) % i
+ 1];
}
}
}
nrowZ = i * nrowX;
ncolZ = ncolX;
}
return z;
}
static int[][] combn(int[] x, int n, int m) {
int e, h, i, j, nmmp1, lenr;
int[] a = new int[m + 1];
int[] r = new int[m + 1];
int count = (int) (factorial(n) / factorial(m) / factorial(n - m));
int[][] out = new int[m + 1][count + 1];
e = 0;
h = m;
for (i = 1; m >= i; i++) {
a[i] = i;
r[i] = x[i];
}
lenr = r.length - 1;
for (j = 1; count >= j; j++) {
for (i = 1; lenr >= i; i++) {
out[i][j] = r[i];
}
}
i = 2;
nmmp1 = n - m + 1;
while (a[1] != nmmp1) {
if (e < n - h) {
h = 1;
e = a[m];
} else {
e = a[m - h];
h++;
}
for (j = 1; h >= j; j++) {
a[m - h + j] = e + j;
}
for (j = 1; m >= j; j++) {
out[j][i] = x[a[j]];
}
i++;
}
return out;
}
}
相異なる素数の足し算で
締め切りが 2017/05/23 10:00 AM なので,その 1 分後に投稿されるように予約
【概要】
整数を、ある範囲の相異なる素数の足し算で表現することを考えます。
例えば、39 を 3以上19以下の、相異なる素数のみを使った足し算で表現する方法は、
3+5+7+11+13
3+17+19
7+13+19
の3通りあります(つまり、順序が異なるだけのものは同一とみなします)。
「39」、「3〜19」 のような情報を与えますので、場合の数(この例だと 3)を計算するプログラムを書いてください。
【入出力】
入力は
39 3 19
のような感じです。
空白区切りで、合計、足し算に使う数の最小値、足し算に使う数の最大値 が並んでいます。
出力は、
3
のような感じで、普通に10進数で出力してください。
【例】
入力 出力
39 3 19 3
70 9 30 2
40 21 39 0
【補足】
不正な入力に対処する必要はありません。
合計は、1以上 100 以下の整数です。
足し算に使う数の最小値は 1 以上の整数で、足し算に使う数の最大値は最小値以上 100 以下の整数です。
ライブラリなどに素数の判定や列挙を行う関数などがある場合、遠慮なく使っていただいて構いません。
====================================
R では実行時間がちょっと掛かりすぎるので,Java で書いたら OK
R では
f = function(x, begin, end) {
mx = end
tbl = 1:mx
tbl[1] = 0
for (i in 2:floor(sqrt(mx))) {
if (tbl[i]) {
mx2 = mx%/%i
tbl[2:mx2 * i] = 0
}
}
prime = tbl[tbl > 0]
prime = prime[prime >= begin]
ans = 0
m = length(prime)
if (m != 0) {
for (n in 1:min(9, m)) {
y = combn(m, n, function(z) prime[z])
if (length(dim(y)) == 1) {
y = matrix(y, 1)
}
y = colSums(y)
# if (sum(y > x) == length(y)) {
# break
# }
# dump(c(n, sum(y == x)))
ans = ans + sum(y == x)
}
}
cat(ans)
}
f(1, 100, 100) # 0
f(3, 3, 3) # 1
f(63, 27, 27) # 0
f(12, 5, 7) # 1
f(72, 25, 46) # 2
f(59, 6, 58) # 6
f(84, 25, 61) # 3
f(79, 13, 43) # 5
f(88, 10, 49) # 7
f(20, 2, 20) # 4
f(72, 3, 29) # 8
system.time(f(100, 1, 100)) # 198
Java では
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
int x, begin, end;
if (false) {
x = 100;
begin = 1;
end = 100;
// x = 1; begin = 100; end = 100;
// x = 3; begin = 3; end = 3;
// x = 63; begin = 27; end = 27;
// x = 12; begin = 5; end = 7;
// x = 72; begin = 25; end = 46;
// x = 59; begin = 6; end = 58;
// x = 84; begin = 25; end = 61;
// x = 79; begin = 13; end = 43;
// x = 88; begin = 10; end = 49;
// x = 20; begin = 2; end = 20;
// x = 72; begin = 3; end = 29;
} else {
Scanner cin = new Scanner(System.in);
String line;
String[] line3 = new String[3];
line = cin.nextLine();
line3 = line.split(" ");
x = Integer.parseInt(line3[0]);
begin = Integer.parseInt(line3[1]);
end = Integer.parseInt(line3[2]);
}
f(x, begin, end);
}
static void f(int x, int begin, int end) {
int i, j, k;
int[] PRIME = prime(end);
int[] vec = new int[PRIME.length];
int count = 0;
int ans = 0;
boolean found;
for (i = 1; i < PRIME.length; i++) {
if (PRIME[i] >= begin && end >= PRIME[i]) {
vec[++count] = PRIME[i];
}
}
for (k = 1; count >= k; k++) {
int size = (int) (factorial(count) / factorial(k) / factorial(count
- k));
int[][] z = new int[k + 1][size + 1];
z = combn(vec, count, k);
int big = 0;
for (j = 1; size >= j; j++) {
int sum = 0;
for (i = 1; k >= i; i++) {
sum += z[i][j];
}
if (sum > x) {
big++;
} else if (sum == x) {
ans++;
// System.out.println(k+", "+ans);
}
}
// System.out.println(" big="+big+" size="+size+" count="+count+" k="+k);
if (big == size - 1) {
break;
}
}
System.out.println(ans);
}
static double factorial(int n) {
int i;
double result = 1;
for (i = 1; n >= i; i++) {
result *= i;
}
return result;
}
static int[][] combn(int[] x, int n, int m) {
int e, h, i, j, nmmp1, lenr;
int[] a = new int[m + 1];
int[] r = new int[m + 1];
int count = (int) (factorial(n) / factorial(m) / factorial(n - m));
int[][] out = new int[m + 1][count + 1];
e = 0;
h = m;
for (i = 1; m >= i; i++) {
a[i] = i;
r[i] = x[i];
}
lenr = r.length - 1;
for (j = 1; count >= j; j++) {
for (i = 1; lenr >= i; i++) {
out[i][j] = r[i];
}
}
i = 2;
nmmp1 = n - m + 1;
while (a[1] != nmmp1) {
if (n - h > e) {
h = 1;
e = a[m];
} else {
e = a[m - h];
h++;
}
for (j = 1; h >= j; j++) {
a[m - h + j] = e + j;
}
for (j = 1; m >= j; j++) {
out[j][i] = x[a[j]];
}
i++;
}
return out;
}
static int[] prime(int m) {
int i, j, count;
int[] tbl = new int[m + 1];
for (i = 1; m >= i; i++) {
tbl[i] = i;
}
tbl[1] = 0;
for (i = 2; Math.sqrt(m) >= i; i++) {
if (tbl[i] != 0) {
for (j = 2 * i; m >= j; j += i) {
tbl[j] = 0;
}
}
}
count = 0;
for (i = 2; m >= i; i++) {
if (tbl[i] != 0) {
count++;
}
}
int[] tbl2 = new int[count + 1];
count = 1;
for (i = 2; m >= i; i++) {
if (tbl[i] != 0) {
tbl2[count++] = tbl[i];
}
}
return tbl2;
}
}
「ロンリー・ルーク」問題
締め切りが 2017/05/18 10:00 AM なので,その 1 分後に投稿されるように予約
設問
自然数 n, k に対し、縦横 n×n のマス目にチェスのルークの駒を k 個配置することを考えます。
このとき、自身から見て上下方向・左右方向のいずれにも他の駒が存在しないような駒を「はぐれルーク」と呼びます。
例えば以下は、(n, k)=(4, 5) のときの駒の配置例を示しています。
それぞれ、はぐれルークを灰色丸、そうでないルークを青色丸で示しています。
また、はぐれルークの個数は、左図では 1 個、右図では 2 個であることが分かります。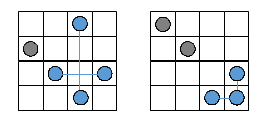
さて、1 つのマスに 2 個以上の駒を置かないよう、ランダムに駒を配置します。
このとき、はぐれルークの個数の期待値を F(n, k) と定義します。
例えば F(2, 2)=2/3 です。
可能な駒の配置は以下の 6 通りです。このうち真ん中の 2 通りでのはぐれルークの個数は 2 個で、他の 4 通りでは 0 個です。
したがって期待値は、0×(4/6)+2×(2/6) = 2/3 となります。
同様に、F(2, 1)=1, F(4, 2)=1.2, F(3, 3)=0.642…, F(4, 5)=0.461…, F(4, 11)=0 となることが確かめられます。
さらに、自然数 n, m に対し、1 ≦ k ≦ m の範囲の自然数 k に対する F(n, k) の和を G(n, m) と定義します。
例えば、G(2, 2)=5/3, G(4, 3)=3.228…, G(4, 5)=4.428… となることが確かめられます。
また、10^3×G(n, m) の整数部分を H(n, m) と定義します。
例えば、H(2, 2)=1666, H(4, 3)=3228, H(4, 5)=4428 です。
標準入力から、自然数 n と m (1 ≦ n ≦ 4, 1 ≦ m ≦ n^2)が半角空白区切りで与えられます。
標準出力に H(n, m) の値を出力するプログラムを書いてください。
なお全てのテストケースにおいて、10^3×G(n, m) の値と、最も近い整数値との差の絶対値は 10^(-3) 以上であることが保証されています。
===================================================
R で簡単に書けるが,計算時間は数秒かかる。
bincombinations = function(p) { # library(e1071) にある
retval = matrix(0, nrow = 2^p, ncol = p)
for (n in 1:p) {
retval[, n] = rep(c(rep(0, (2^p/2^n)), rep(1, (2^p/2^n))),
length = 2^p)
}
retval
}
f = function(n, m) {
check = function(x) {
rSum = rowSums(x) == 1
cSum = colSums(x) == 1
sum(outer(rSum, cSum, "&") & x)
}
len = 2^(n*n)
a = array(t(bincombinations(n*n)), dim=c(n, n, len))
s = apply(a, 3, sum)
sm = apply(a, 3, check)
tbl = table(s, sm)
rSum = rowSums(tbl)
F = colSums(t(tbl / rSum) * 0:n)
G = cumsum(F)
ans = G[m+1]
H = floor(ans*1000)
cat(H)
}
# s = scan(file("stdin", "r"))
# f(s[1], s[2])
#f(2, 3) # 1666
#f(3, 3) # 2642
#f(3, 4) # 2928
#f(4, 4) # 3967
#f(4, 7) # 4797
#f(4, 16) # 4857, 2.922 seq.
Java で書けば,計算は一瞬で終わるが,プログラムを書くのが面倒だ。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
if (true) {
System.out.println(f(2, 3)); // 1666
System.out.println(f(3, 3)); // 2642
System.out.println(f(3, 4)); // 2928
System.out.println(f(4, 4)); // 3967
System.out.println(f(4, 7)); // 4797
System.out.println(f(4, 16)); // 4857
} else {
Scanner cin = new Scanner(System.in);
String line;
String[] line2 = new String[2];
line = cin.nextLine();
line2 = line.split(" ");
int n = Integer.parseInt(line2[0]);
int m = Integer.parseInt(line2[1]);
System.out.println(f(n, m));
}
}
static int pow2(int n) {
int i, res = 1;
for (i = 0; i < n; i++) {
res *= 2;
}
return res;
}
static int check(int[][] subMat, int n) {
int i, j;
int [] rowSums = new int[n];
int [] colSums = new int[n];
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
rowSums[i] += subMat[i][j];
colSums[j] += subMat[i][j];
}
}
int sum = 0;
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
if (subMat[i][j] == 1 && rowSums[i] == 1 && colSums[j] == 1) {
sum++;
}
}
}
return sum;
}
static int f(int n, int m) {
int i, j, k;
int[][] ary = bincombinations(n * n);
int[][] subMat = new int[n][n];
double[][] tbl = new double[n * n + 1][n + 1];
for (i = 0; i < pow2(n * n); i++) {
int s = 0;
for (j = 0; j < n * n; j++) {
s += ary[i][j];
}
for (j = 0; j < n; j++) {
for (k = 0; k < n; k++) {
subMat[j][k] = ary[i][j * n + k];
}
}
tbl[s][check(subMat, n)]++;
}
double ans = 0;
for (i = 0; m >= i; i++) {
int rSum = 0;
for (j = 0; j < n + 1; j++) {
rSum += tbl[i][j];
}
for (j = 0; j < n + 1; j++) {
tbl[i][j] /= rSum;
ans += tbl[i][j] * j;
}
}
return (int) (ans * 1000);
}
static int[] c(int[] x, int[] y) {
int lenX = x.length;
int lenY = y.length;
int i;
int[] res = new int[lenX + lenY];
for (i = 0; i < lenX; i++) {
res[i] = x[i];
}
for (i = 0; i < lenY; i++) {
res[lenX + i] = y[i];
}
return res;
}
static int[] rep(int[] x, int len) {
int i, pos = 0;
int[] res = new int[len];
int m = x.length;
for (;;) {
for (i = 0; i < m; i++) {
res[pos++] = x[i];
if (pos == len) {
return res;
}
}
}
}
static int[][] bincombinations(int p) {
int[] zero = { 0 };
int[] one = { 1 };
int m = pow2(p);
int[][] ary = new int[m][p];
int[] x = new int[m];
int n, i;
for (n = 0; n < p; n++) {
x = rep(c(rep(zero, pow2(p - n - 1)), rep(one, pow2(p - n - 1))), pow2(p));
for (i = 0; i < m; i++) {
ary[i][n] = x[i];
}
}
return ary;
}
}
取られたら取り返す!
締め切りが 2017/05/09 10:00 AM なので,その 1 分後に投稿されるように予約
設問
卓球では11点先取、バレーボールでは25点先取で1セットを取るようなルールがあります。
ただ、この得点よりも1点少ない得点以上の得点で同点となると「デュース」と呼ばれることがあり、その後は2点差を付けるまで続けられます。
(卓球やバドミントンにはデュースという言葉はありませんが、同様に進められます。)
A と B がn 点先取の試合を行ったとき、それぞれの点数が a 対 b になるまでの点数の推移を考えます。
例えば、n = 3, a = 4, b = 2 のとき、点数の推移は以下の6通りがあります。
(下記の記号は点数を取った側を表すものとします。)
(1) A -> A -> B -> B -> A -> A
(2) A -> B -> A -> B -> A -> A
(3) A -> B -> B -> A -> A -> A
(4) B -> A -> A -> B -> A -> A
(5) B -> A -> B -> A -> A -> A
(6) B -> B -> A -> A -> A -> A
このとき、以下のように点数が推移することはありません。
(途中で3点を先取してしまい、セットが終了するため)
A -> A -> B -> A -> B -> A
標準入力から n, a, b がスペース区切りで与えられるとき、点数の推移が何通りあるかを求め、標準出力に出力してください。
なお、n, a, b はいずれも25以下の正の整数とします。
【入出力サンプル】
標準入力
3 4 2
標準出力
6
=================================================
例によって,サイズの小さい場合について,馬鹿正直に計算するプログラムを書き,結果から規則性を見いだす。
n = 6 の場合については下図のようになる。
水色の部分は i, j > 1 において,x[i, j] = x[i-1, j] + x[i, j-1]
黄色の部分は近隣のコピー(コピーの順番に注意)
ということで,一般的には
f = function(n, a, b) {
x = matrix(0, 28, 28) # 計算途中で添え字が溢れないように +2
for (i in 1:n-1) {
for (j in 1:n-1) {
x[i+1, j+1] = choose(i+j, i)
}
}
x[n+1, 1:n] = x[1:n, n+1] = x[n, 1:n]
for (i in n:26) {
x[i, i+1:2] = x[i+1:2, i] = x[i, i] = x[i-1, i] + x[i, i-1]
}
cat(x[a+1, b+1])
}
# s = scan(file("stdin", "r"))
# f(s[1], s[2], s[3])
f(3, 4, 2) # 6
f(10, 9, 8) # 24310
f(15, 0, 14) # 1
f(15, 17, 20) # 0
f(11, 25, 24) # 3027042304
140問目!素数列から抜き出してつぶやこう?
締め切りが 2017/05/02 10:00 AM なので,その 1 分後に投稿されるように予約
設問
今週のアルゴリズムも140問目!
「140」といえばTwitterにおけるつぶやきの文字数の上限です。
m 以上 n 以下の素数を一列に並べ、その中から連続した数字列を最長140文字で抜き出したとき、最初と最後の数字が同じで、含まれる数の和が最大になるものを求め、その和を出力してください。
例えば、m = 5, n = 30 のとき、
57111317192329
という数字列の中から、最初と最後の数字が同じで、長いものを抜き出すと、含まれる数の和は
7111317 -> 21
1113171 -> 15
3171923 -> 26
92329 -> 25
232 -> 7
となりますので、最大なのは26です。
標準入力から m と n がスペース区切りで与えられるとき、和の最大値を求め、標準出力に出力してください。
なお、m と n は 1 < m < n < 100000を満たす整数とします。
【入出力サンプル】
標準入力
5 30
標準出力
26
−−−−−−−−−−
素直にプログラムし,なんの最適化もしなかったが,計算時間も制限内に収まっていた
f = function(m, n) {
mx = n # エラトステネスの篩で素数列生成
tbl = 1:mx
tbl[1] = 0
for (i in 2:floor(sqrt(mx))) {
if (tbl[i]) {
mx2 = mx %/% i
tbl[2:mx2*i] = 0
}
}
prime <- tbl[tbl >= m] # m 以上,n 以下の素数
x = as.integer(unlist(strsplit(paste(prime, collapse=""), ""))) # 繋いでばらす
maxSum = 0
for (i in seq_along(x)) {
y = x[i:min(i+139, length(x))] # i 番目から 140 個以内の数字列
z = which(y == x[i]) # 最初と同じ数字のある場所
s = sum(y[1:max(z)]) # 最初から最後の位置までの数字の和
maxSum = max(s, maxSum) # 最大のものを記録
}
cat(maxSum)
}
# s = scan(file("stdin", "r"), quiet=TRUE)
# f(s[1], s[2])
f(5, 30) # 26
f(2, 100) # 204
f(100, 10000) # 930
f(10000, 50000) # 860
f(2, 99999) # 1019


















