この記事の最後に掲載するシミュレーションプログラムを作ってみた。
プログラムは,群の平均値をベクトル,各群共通の標準偏差を引数に持つ。
power.anova.test() または pwr.anova.test() で所要の power を得るためのサンプルサイズ n を求める。
シミュレーションデータを生成し,一元配置分散分析により p.value < sig.level となる確率を集計する。
この確率が,power のシミュレーション値である。
実行例
***** シミュレーションのあらまし
群の数 k = groups = 3
各群の平均値 = 145, 152, 163
標準偏差は各群共通 sd = 10
***** power.anova.test() で計算してみる
between.var は平均値の不偏分散 bv = var(group.means) = 82.33333333
within.var は各群共通の標準偏差の二乗(つまり分散) sd^2 = 100
power.anova.test(groups=k, between.var=bv, within.var=sd^2, sig.level=sig.level, power=power)
Balanced one-way analysis of variance power calculation
groups = 3
n = 6.953779905
between.var = 82.33333333
within.var = 100
sig.level = 0.05
power = 0.8
NOTE: n is number in each group
power >= 0.8 となるのは n = 7 (計算された n = 6.953779905 )
***** pwr.anova.test() でも計算してみる
pwr.anova.test() で使われる効果量 f = sqrt(bv * (k-1)/k) / sd = 0.740870359
pwr.anova.test(k=k, f=f, sig.level=sig.level, power=power)
Balanced one-way analysis of variance power calculation
k = 3
n = 6.953782438
f = 0.740870359
sig.level = 0.05
power = 0.8
NOTE: n is number in each group
同じ n が得られる。
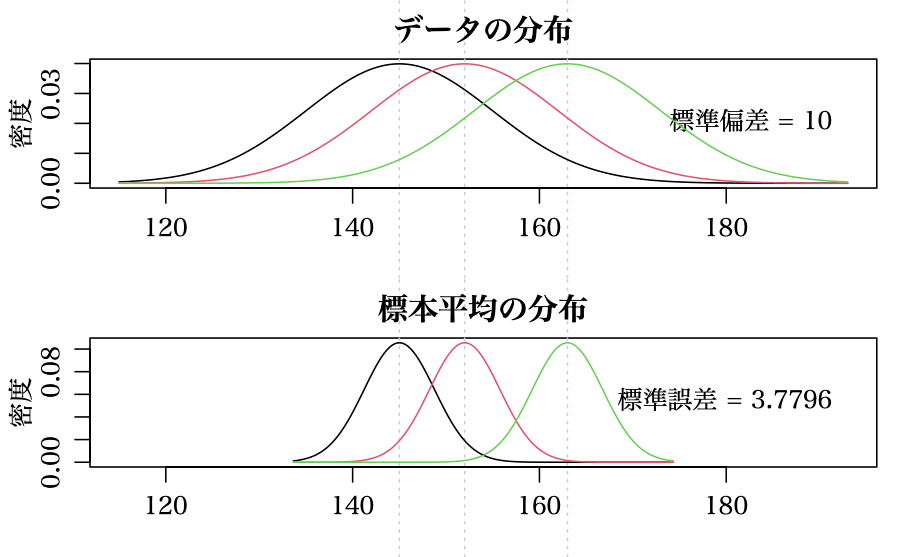
***** 1000 回のシミュレーション
各群の平均値が 145, 152, 163 で,各群共通の標準偏差が 10 である 3 群のシミュレーションデータ生成と分析
効果量 f の平均値 = 0.8039049106 理論値は上述の f = 0.740870359
検出力 power = 0.787 理論値は 0.8
***** ちなみに,power.anova.test() での within.var は,シミュレーションの 1 試行例では,
各群の不偏分散 = 188.795983946315, 131.296455655148, 27.5106187727577
各群の不偏分散の平均 = mean(group.vars) = 115.8676861 ==> within.var
***** anova(aov()) の結果例と照合
Reiduals の行の Mean Sq の数値と一致
Analysis of Variance Table
Response: x
Df Sum Sq Mean Sq F value Pr(>F)
g 2 2832.0374 1416.01871 12.221 0.00044391
Residuals 18 2085.6184 115.86769
プログラムソース
sim = function(n, group.means, sd = 1, sig.level = 0.05, power = 0.8, trial = 1000, plot.flag = TRUE) {
k = length(group.means)
cat("***** シミュレーションのあらまし\n")
cat("群の数 k = groups =", k, "\n")
cat("各群の平均値 =", paste(group.means, collapse = ", "), "\n")
cat("標準偏差は各群共通 sd =", sd, "\n")
if (plot.flag) {
layout(matrix(1:2, 2))
old = par(mgp = c(1.8, 0.8, 0), mar = c(3, 3, 2, 1))
x = seq(min(group.means) - 3 * sd, max(group.means) + 3 * sd, length = 200)
range.x = range(x)
range.y = range(dnorm(x, mean = group.means[1], sd = sd))
plot(0, 0, xlim = range.x, ylim = range.y, type = "n", xlab = "", ylab = "密度")
abline(v = group.means, xpd = TRUE, col = "gray80", lty = 3)
title("データの分布")
text(range.x[2], mean(range.y), paste("標準偏差 =", sd), pos = 2)
for (i in 1:k) {
y = dnorm(x, mean = group.means[i], sd = sd)
lines(x, y, col = i)
}
}
cat("***** power.anova.test() で計算してみる\n")
bv = var(group.means)
cat("between.var は平均値の不偏分散 bv = var(group.means) =", bv, "\n")
cat(" within.var は各群共通の標準偏差の二乗(つまり分散) sd^2 =", sd^2, "\n")
cat("power.anova.test(groups=k, between.var=bv, within.var=sd^2, sig.level=sig.level, power=power)\n")
pat = power.anova.test(groups = k, between.var = bv, within.var = sd^2,
sig.level = sig.level, power = power)
print(pat)
n = ceiling(pat$n)
cat("power >= ", power, "となるのは n =", n, "(計算された n =", pat$n, ")\n")
cat("***** pwr.anova.test() でも計算してみる\n")
f = sqrt(bv * (k - 1)/k)/sd
cat("pwr.anova.test() で使われる効果量 f = sqrt(bv * (k-1)/k) / sd =", f, "\n")
cat("pwr.anova.test(k=k, f=f, sig.level=sig.level, power=power)\n")
print(pwr.anova.test(k = k, f = f, sig.level = sig.level, power = power))
if (plot.flag) {
x = seq(min(group.means) - 3 * sd/sqrt(n),
max(group.means) + 3 * sd/sqrt(n), length = 200)
range.y = range(dnorm(x, mean = group.means[1], sd = sd/sqrt(n)))
plot(0, 0, xlim = range.x, ylim = range.y, type = "n", xlab = "", ylab = "密度")
abline(v = group.means, xpd = TRUE, col = "gray80", lty = 3)
title("標本平均の分布")
text(range.x[2], mean(range.y), paste("標準誤差 =", round(sd/sqrt(n), 4)), pos = 2)
for (i in 1:k) {
y = dnorm(x, mean = group.means[i], sd = sd/sqrt(n))
lines(x, y, col = i)
}
layout(1)
par(old)
}
g = factor(rep(1:k, n))
p.value = numeric(trial)
f = numeric(trial)
cat("*****", trial, "回のシミュレーション\n")
cat("各群の平均値が", paste(group.means, collapse = ", "), "で,各群共通の標準偏差が",
sd, "である", k, "群のシミュレーションデータ生成と分析\n")
for (i in 1:trial) {
x = rnorm(k * n, mean = group.means, sd = sd)
p.value[i] = oneway.test(x ~ g, var.equal = TRUE)$p.value
MS = anova(aov(x ~ g))$"Mean Sq"
f[i] = sqrt(MS[1]/n * (k - 1)/k/MS[2])
}
cat("効果量 f の平均値 =", mean(f), "\n")
cat("検出力 power =", mean(p.value < sig.level), "\n")
cat("***** ちなみに,within.var は,シミュレーションの 1 試行では,\n")
group.vars = tapply(x, g, var)
wv = mean(group.vars)
cat("各群の不偏分散 =", paste(group.vars, collapse = ", "), "\n")
cat("各群の不偏分散の平均 = mean(group.vars) =", wv, " ==> within.var\n")
cat("***** anova(aov()) の結果例と照合\n")
cat("Reiduals の行の Mean Sq の数値と一致\n")
print(anova(aov(x ~ g)))
}
library(pwr)
options(digits = 10)
sim(group.means = c(145, 152, 163), sd = 10, trial = 1000, plot = TRUE)