バラバラのマトリョーシカを一つに合体
締め切りが 2017/08/29 10:00 AM なので,その 1 分後に投稿されるように予約
設問
大きさが異なる m 個のマトリョーシカ人形があります。
マトリョーシカ人形は、大きな人形の内部に、それより小さな人形を入れられます。
今、3つのテーブルの上に m 個のマトリョーシカ人形がバラバラに置かれています。
ただし、一つのテーブル上のマトリョーシカ人形は、必ず重ねて置かれています。
つまり、見えているのは最大で3つの人形です。
これらの人形からいずれか一つを選択して最も外側の人形を外し、
・ほかの人形に付け替える、
・他の人形が置かれていないテーブルに移す
のいずれかの作業を繰り返して、最短回数ですべての人形が一つのテーブルに揃うようにしたいと思います。
(つまり、一つの人形の中にすべての人形が入るようにする。)
ただし、一回に一つの人形しか作業できません。
当然、大きな人形の外側に小さな人形を付けることもできません。
標準入力から整数 m, n がスペース区切りで与えられたとき、ちょうど n 回で作業が完了するような初期配置が何通りあるかを求め、標準出力に出力してください。
なお、m, n はともに正の整数で、m < 15, n < 1600 を満たすものとします。
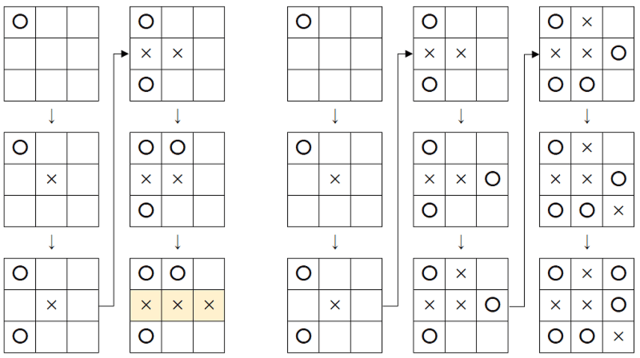
例えば、m=4のとき、最初に以下の左上の状態になっていると、図のように作業に6回かかります。
ちょうど6回で作業が完了するのは、以下の2通りですので、 m = 4, n = 6 のときは標準出力に2を出力します。
【入出力サンプル】
標準入力
4 6
標準出力
2
==================================================
ページの終わりに書くように,一行解がある。
m が 2 以上のときは,n = 1 が 1 通りずつ。
m が 3 以上のとき,水色の部分は m-1 のときの水色と黄色の部分を併せたものと同じ,黄色の部分はそれを 2 倍したもの。
2次元の配列にする必要はないが,わかりやすくするため。
実際には,ベクトルでよい。
f = function(m, n) {
a = numeric(2^(m-1)-1)
a[1] = 1
b = a[1]
for (M in 3:m) {
begin1 = 2^(M-2)
end1 = 3*2^(M-3)-1
begin2 = 3*2^(M-3)
end2 = 2^(M-1)-1
a[begin1:end1] = b
a[begin2:end2] = 2*b
b = a[begin1:end2]
}
cat(a[n])
}
# arg = scan(file("stdin", "r"))
# f(arg[1], arg[2])
f(4, 6) # 2
f(5, 13) # 4
f(7,63) # 32
f(10, 499) # 64
f(12, 1599) # 128
いつものオンライン整数列大辞典にある。
オンライン整数列大辞典 https://oeis.org/A048896
引数 m は不要
f = function(n) {
cat(2^(n-1-sum(floor(n/2^(1:10)))))
}