算額(その834)
本件は,算額(その320)の再分析である。数値解ではなく解析解を求めたものである。
https://blog.goo.ne.jp/r-de-r/e/6de81f639fc17da2712fa756f3926dc5
長野県長野市戸隠 戸隠山中院権現堂 安永5年(1776)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
外円の中に中円1個,小円2個が入っている。外円の面積から中円・小円の面積を引くと 120 歩である。また,中円と小円の直径の差は 5 寸である。小円の直径を求めよ。
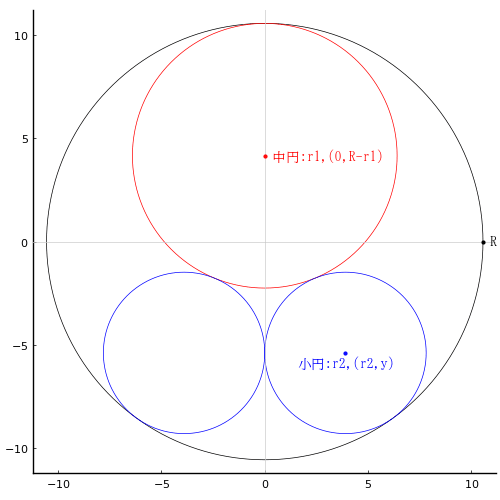
外円の半径と中心座標を R, (0, 0)
中円の半径と中心座標を r1, (0, R - r1)
小円の半径と中心座標を r2, (r2, y)
r1 = r2 + 直径差//2
小円が外円に内接することから y = -sqrt(R^2 - 2R*r2)
とおき,以下の連立方程式を解く。
なお,eq1 の 3 は,この算額で用いる円周率の近似値である(黒積の値 120 はこれによっている)。
eq2 は中円と小円が外接することを表している。
黒積と,直径差の具体値に対して解を求める。
include("julia-source.txt");
using SymPy
@syms R::positive, r1::positive, r2::positive, y::negative,
黒積::positive, 直径差::positive;
# r1 = r2 + 直径差//2
# r2^2 + y^2 = (R - r2)^2 # 小円が外円に内接することから
# y = -sqrt(R^2 - 2R*r2)
黒積 = 120
直径差 = 5
eq1 = 3*(R^2 - ((r2 + 直径差//2)^2 + 2r2^2)) - 黒積 |> expand |> simplify;
eq2 = r2^2 + (R - (r2 + 直径差//2) - (-sqrt(R^2 - 2R*r2)))^2 - ((r2 + 直径差//2) + r2)^2 |> expand |> simplify;
res = solve([eq1, eq2], (r2, R))
1-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
(CRootOf(44*x^6 + 440*x^5 + 1420*x^4 + 250*x^3 - 19400*x^2 - 107875*x - 185000, 1), sqrt(20*CRootOf(44*x^6 + 440*x^5 + 1420*x^4 + 250*x^3 - 19400*x^2 - 107875*x - 185000, 1) + 12*CRootOf(44*x^6 + 440*x^5 + 1420*x^4 + 250*x^3 - 19400*x^2 - 107875*x - 185000, 1)^2 + 185)/2)
解は多項式の形で与えられる。数値としての解は .evalf() によって得ることができる。
小円の半径は 3.90671194097833(直径は 7.81342388195666)である。
res[1][1] |> println # r2
res[1][1].evalf() |> println # r2
2res[1][1].evalf() |> println # 2r2
CRootOf(44*x^6 + 440*x^5 + 1420*x^4 + 250*x^3 - 19400*x^2 - 107875*x - 185000, 1)
3.90671194097833
7.81342388195666
外円の半径は 10.5627058216273(直径は 21.1254116432546)である。
res[1][2] |> println # R
res[1][2].evalf() |> println # R
2res[1][2].evalf() |> println # R
sqrt(20*CRootOf(44*x^6 + 440*x^5 + 1420*x^4 + 250*x^3 - 19400*x^2 - 107875*x - 185000, 1) + 12*CRootOf(44*x^6 + 440*x^5 + 1420*x^4 + 250*x^3 - 19400*x^2 - 107875*x - 185000, 1)^2 + 185)/2
10.5627058216273
21.1254116432546
r1, y はそれぞれ 6.4067119409783295,-5.388864105676991 である。
r1 = 3.90671194097833 + 直径差//2
r1 |> println
y = -sqrt(10.5627058216273^2 - 2*10.5627058216273*3.90671194097833)
y |> println
6.4067119409783295
-5.388864105676991
--- 別解
SymPy の能力的に,黒積,直径差を定数のままで方程式を解くことができないので,手動で解を求める。
include("julia-source.txt");
using SymPy
@syms R::positive, r1::positive, r2::positive, y::negative,
黒積::positive, 直径差::positive;
# r1 = r2 + 直径差//2
# r2^2 + y^2 = (R - r2)^2
# y = -sqrt(R^2 - 2R*r2)
eq1 = 3*(R^2 - ((r2 + 直径差//2)^2 + 2r2^2)) - 黒積 |> expand |> simplify;
eq2 = r2^2 + (R - (r2 + 直径差//2) - (-sqrt(R^2 - 2R*r2)))^2 - ((r2 + 直径差//2) + r2)^2 |> expand |> simplify;
println(eq1, ", # eq1")
println(eq2, ", # eq2")
3*R^2 - 9*r2^2 - 3*r2*直径差 - 3*直径差^2/4 - 黒積, # eq1
2*R^(3/2)*sqrt(R - 2*r2) - 2*sqrt(R)*r2*sqrt(R - 2*r2) - sqrt(R)*直径差*sqrt(R - 2*r2) + 2*R^2 - 4*R*r2 - R*直径差 - 2*r2^2 - r2*直径差, # eq2
まず,eq1 を R について解く。
R = sqrt(108*r2^2 + 36*r2*直径差 + 9*直径差^2 + 12*黒積)/6
res1 = solve(eq1, R) # R
1-element Vector{Sym{PyCall.PyObject}}:
sqrt(108*r2^2 + 36*r2*直径差 + 9*直径差^2 + 12*黒積)/6
eq2 の R に,今求めた sqrt(108*r2^2 + 36*r2*直径差 + 9*直径差^2 + 12*黒積)/6 を代入する。
eq3 = eq2(R => res1[1]) |> simplify
eq3 |> println
4*r2^2 + r2*直径差 - r2*sqrt(-12*r2 + sqrt(3)*sqrt(36*r2^2 + 12*r2*直径差 + 3*直径差^2 + 4*黒積))*(108*r2^2 + 36*r2*直径差 + 9*直径差^2 + 12*黒積)^(1/4)/3 - 2*r2*sqrt(108*r2^2 + 36*r2*直径差 + 9*直径差^2 + 12*黒積)/3 + 直径差^2/2 - 直径差*sqrt(-12*r2 + sqrt(3)*sqrt(36*r2^2 + 12*r2*直径差 + 3*直径差^2 + 4*黒積))*(108*r2^2 + 36*r2*直径差 + 9*直径差^2 + 12*黒積)^(1/4)/6 - 直径差*sqrt(108*r2^2 + 36*r2*直径差 + 9*直径差^2 + 12*黒積)/6 + 2*黒積/3 + sqrt(-12*r2 + sqrt(3)*sqrt(36*r2^2 + 12*r2*直径差 + 3*直径差^2 + 4*黒積))*(108*r2^2 + 36*r2*直径差 + 9*直径差^2 + 12*黒積)^(3/4)/18
黒積,直径差に具体的数値を代入する。
eq4 = eq3(黒積 => 120, 直径差 => 5)
eq4 |> println
4*r2^2 - r2*sqrt(-12*r2 + sqrt(3)*sqrt(36*r2^2 + 60*r2 + 555))*(108*r2^2 + 180*r2 + 1665)^(1/4)/3 - 2*r2*sqrt(108*r2^2 + 180*r2 + 1665)/3 + 5*r2 + sqrt(-12*r2 + sqrt(3)*sqrt(36*r2^2 + 60*r2 + 555))*(108*r2^2 + 180*r2 + 1665)^(3/4)/18 - 5*sqrt(-12*r2 + sqrt(3)*sqrt(36*r2^2 + 60*r2 + 555))*(108*r2^2 + 180*r2 + 1665)^(1/4)/6 - 5*sqrt(108*r2^2 + 180*r2 + 1665)/6 + 185/2
eq4 は r2 だけを含むので,solve で解いて r2 を得る。
実際には CrootOf() の形式で出てくるが,これは,カッコ内の多項式の根を求めるということを意味している。この多項式は eq4 のルートを外したものになっている。
res2 = solve(eq4, r2)
1-element Vector{Sym{PyCall.PyObject}}:
CRootOf(44*x^6 + 440*x^5 + 1420*x^4 + 250*x^3 - 19400*x^2 - 107875*x - 185000, 1)
実際の値は .evalf() すればよい。
小円の直径は 7.81342388195666 である。
@printf("小円の半径 = %.15g; 小円の直径 = %.15g\n", res2[1].evalf(), 2res2[1].evalf())
小円の半径 = 3.90671194097833; 小円の直径 = 7.81342388195666
r2 がわかれば,R, y, r1 を順次計算することができる。
黒積 = 120
直径差 = 5
r2 = 3.90671194097833
R = sqrt(108*r2^2 + 36*r2*直径差 + 9*直径差^2 + 12*黒積)/6
y = -sqrt(R^2 - 2R*r2)
r1 = r2 + 直径差//2
@printf("R = %.15g; r1 = %.15g; r2 = %.15g; y = %.15g\n", R, r1, r2, y)
R = 10.5627058216273; r1 = 6.40671194097833; r2 = 3.90671194097833; y = -5.38886410567701
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
@printf("R = %.6f; r1 = %.6f; r2 = %.6f; y = %.6f\n", R, r1, r2, y)
@printf("黒積 = %g\n", pi*(R^2 - (r1^2 + 2r2^2)))
println("小円の直径 = $(Float64(2r2))")
plot()
circle(0, 0, R, :black)
circle(0, R - r1, r1)
circle2(r2, y, r2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, R - r1, " 中円:r1,(0,R-r1)", :red, :left, :vcenter)
point(R, 0, " R", :black, :left, :vcenter)
point(r2, y, "小円:r2,(r2,y)", :blue, :center, delta=-delta/2)
end
end;


















