Julia に翻訳--004

#=
Julia の修行をするときに，いろいろなプログラムを書き換えるのは有効な方法だ。
以下のプログラムを Julia に翻訳してみる。

正規確率紙に累積相対度数をプロットする
http://aoki2.si.gunma-u.ac.jp/R/npp.html

# 正規確率紙に累積相対度数をプロットする
npp <- function(y, # 度数ベクトル
                x=NULL, # 階級代表値
                plt=TRUE, # データ点をプロットする
                xlab=NULL, # 横軸ラベル
                ylab=NULL, # 縦軸ラベル
                main=NULL) # 図のタイトル
{
        if (length(y) < 3) { # 階級数が2以下のときには正規確率紙のみを出力する
                y <- 1:11
                plt <- FALSE
        }
        y <- cumsum(y)/sum(y) # 累積相対度数
        if (is.null(x)) {
                x = seq(along=y)
        }
        if (is.null(xlab)) xlab <- "観察値"
        if (is.null(ylab)) ylab <- "累積相対度数"
        if (is.null(main)) main <- "正規確率紙"
        probs <- c(0.01, 0.1, 1, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, 95, 99, 99.9, 99.99)/100
        plot(c(x[1], x[length(x)-1]), qnorm(c(probs[1], probs[17])), type="n", xaxt="n", yaxt="n",
                xlab=xlab, ylab=ylab, main=main)
        abline(h=qnorm(probs), v=x, col="grey") # 格子線を引く
        if (plt) { # データ点をプロットする
                points(x, qnorm(y), type="b")
                text(x, qnorm(y), round(y, digit=3)*100, pos=1)
        }
        axis(1, at=x) # 横軸を描く
        axis(2, at=qnorm(probs), labels=probs*100) # 縦軸を描く
}

ファイル名: npp.jl　　関数名:npp

翻訳するときに書いたメモ

scatter! と annotate! の位置関係で図が表示できないというトラブルがあったが，バグか？
annotate! も，書き方によっては引数にベクトルが使えないので，for loopで書かざるを得ない？

=#

using Distributions
using Plots
using Plots.PlotMeasures

function npp(y; x = [], plt = true, leftmargin=2mm,
    xlab = "観察値", ylab = "累積確率", main = "正規確率紙")
 pyplot()
 if length(y) < 3
  y = 1:11
  plt = false
 end
 y = cumsum(y)/sum(y)
 x = length(x) == 0 ? collect(1:length(y)) : x
 probability = [0.01, 0.1, 1, 5, 10, 20, 30, 40, 50,
     60, 70, 80, 90, 95, 99, 99.9, 99.99]/100;
 qnp = quantile(Normal(), probability);
 delta = (x[2] - x[1]) / 2
 p = plot([x[1], x[1], x[end-1]], [qnp[end], qnp[1], qnp[1]],
  xlims = (x[1]-delta, x[end-1]+delta),
  linecolor=:gray,
  linestyle=:dot,
  tickdirection=:out,
  grid=false,
  label="",
  xlabel=xlab,
  ylabel=ylab,
  title=main,
  leftmargin=leftmargin,
  size=(600, 400))
 yticks!(quantile(Normal(), probability), string.(round.(probability, digits=4)))
 hline!(quantile(Normal(), probability), linecolor = :gray, linestyle=:dot, label="")
 vline!(x, linecolor=:gray, linestyle=:dot, label="")
 if plt
  qny = quantile(Normal(), y)
  scatter!(x[1:end-1], qny[1:end-1], markercolor=:black, label="")
  stry = string.(round.(y, digits=3))
  for i = 1:length(x)-1
   annotate!(x[i], qny[i]-0.3, text(stry[i], 8))
  end
 end
 display(p)
end

npp([1, 2, 3, 4, 3, 2, 1])

npp([1, 2, 3, 4, 3, 2, 1], x=collect(160:5:190))

npp(collect(1:21), plt=false)

Julia の小ネタ--004

using Plots でグラフを描いたのだけど，左マージン leftmargin を増やすために leftmargin=5mm と書いても，"mm not defined" と，エラーになるばかり。px とか mm という単位が使えるということなのだけど...

色々調べて，

using Plots.PlotMeasures

を付け加えないといけないと教えられた。

 

漢字出力の不具合解消された R version 4.0.4

R version 4.0.4 Patched (2021-02-17 r80031) で確認

version.string R version 4.0.4 Patched (2021-02-17 r80031)
nickname       Lost Library Book                          
> print("漢字の出力，問題なし！")
[1] "漢字の出力，問題なし！"

 

Julia に翻訳--003

#===============
Julia の修行をするときに，いろいろなプログラムを書き換えるのは有効な方法だ。
以下のプログラムを Julia に翻訳してみる。

データの読み込みと前処理と可視化まで

R/plotlyの忘備録
https://qiita.com/yono2844/items/4a27f8b74dd31e20221d

元のプログラム

R"""
library(plotly)
library(lubridate)
library(dplyr)

# https://archive.ics.uci.edu/ml/datasets/water+treatment+plant
X <- read.csv(file="water-treatment.data", header=FALSE, na.strings="?")
X <- na.omit(X)
X <- X %>% mutate(V1=dmy(X$V1)) %>% arrange(V1)
X <- X %>% mutate_if(is.numeric, scale) %>% mutate_if(is.numeric, as.numeric)

# line-plot
fig <- plot_ly(x=X$V1, y=X$V2, type="scatter", mode="lines", name="V2")
fig <- fig %>% add_trace(x=X$V1, y=X$V3, name="V3")
fig <- fig %>% add_trace(x=X$V1, y=X$V4, name="V4")
fig <- fig %>% add_trace(x=X$V1, y=X$V5, name="V5")
fig <- fig %>% layout(
    xaxis=list(title="Date"),
    yaxis=list(title="Value"))
fig

# Histogram
fig <- plot_ly(x=X$V2, type="histogram")
fig <- fig %>% layout(
    xaxis=list(title="V2"),
    yaxis=list(title="Count")
)
fig
"""

翻訳するときに書いたメモ

なかなか，癖の強いデータファイルである。
dplyr が絡むとなおさら。

x.v1 の変換は，以下のようにしてもよいが，
#x.v1 = replace.(x.v1, "D-"=>"");
#x.v1 = replace.(x.v1, "/90"=>"/1990");
#x.v1 = replace.(x.v1, "/91"=>"/1991");
#x.v1 = Date.(x.v1, DateFormat("d/m/yy")); # 日付データに変換

getdate() を定義するとよい。
x.v1 = getdate.(x.v1)

正規化も for -- end で実質 1 行で書ける。

===============#

using CSV, DataFrames, Dates, StatsBase, Plots
plotly()

function getdate(s)
    a = split.(s, r"[-/]")
    Date(Dates.Year("19"*a[4]), Dates.Month(a[3]), Dates.Day(a[2]))
end

# 欠損値が "?"      missingstring="?"
# 整数データがある   typemap=Dict(Int => Float64) # Julia 特有か（実数に変換しなければ問題ない）
# ヘッダーがない     header="v" .* string.(1:39)
x = CSV.read("water-treatment.data", DataFrame, missingstring="?",
    typemap=Dict(Int => Float64), header="v" .* string.(1:39));
x = dropmissing(x); # 欠損値のある行を削除
x.v1 = getdate.(x.v1); # 日付データの整形
sort!(x, :v1); # しかも日付がソートされていないのでソートする
A = Matrix(x[:, 2:39]); # 正規化
temp = fit(ZScoreTransform, A, dims=1);
x[:, 2:39] = StatsBase.transform(temp, A);

p = plot(x.v1, x.v2, xlabel="Date", ylabel="Value", label="v2");
p = plot!(x.v1, x.v3, label="v3");
p = plot!(x.v1, x.v4, label="v4");
p = plot!(x.v1, x.v5, label="v5")

p = histogram(x.v2, xlabel="v2", ylabel="count", label="")

Julia に翻訳--002

#=
Julia の修行をするときに，いろいろなプログラムを書き換えるのは有効な方法だ。
以下のプログラムを Julia に翻訳してみる。

塗り分け地図を描く
http://aoki2.si.gunma-u.ac.jp/R/color-map.html

ファイル名: colormap.jl
関数名: colormap, colormap1, colormap2, colormap3, colormap4
  rgb(i::Int), rgb(str::String)

翻訳するときに書いたメモ

x = [1,2,3,4,]
append!(x, 5)
はいいのに，
y = [:red, :yellow]
append!(y, :red)
はエラーになる
append!(y, [:red])
なら，通る。何故なんだ！

引数の型が違う関数を同じ関数名で定義できるのは面白い。
rgb(i::Int), rgb(str::String)
colormap1 〜 colormap4 もそのようにするのもよいかも知れないが，混乱しそうなので止めておく。

=#

using Printf, DataFrames, Plots
using FixedPointNumbers, ColorTypes # for RGB

function colormap(codelist; color=repeat([:red], length(codelist)))
 function map0(data; color)
  cont = (data.lon .!= 0) .| (data.lat .!= 0)
  allowmissing!(data)
  data[.!cont, 1] .= missing
  data[.!cont, 2] .= missing

  p = plot(data.lon, data.lat, linecolor=:black, showaxis=false,
             ticks=false, grid=false, aspect_ratio=1, label="")
  start = 1
  k = 0
  for i = 2:size(data, 1)
   if cont[i] == false
    k += 1
    if i-start == 4
     plot!(data.lon[start:(i-1)], data.lat[start:(i-1)], label="")
    else
     plot!(data.lon[start:(i-1)], data.lat[start:(i-1)],
      seriestype=:shape, fillcolor=color[k], label="")
    end
    start = i + 1
   end
  end
  display(p)
 end

 for i in 1:length(codelist)
  if codelist[i] in [15, 28, 47]
   append!(codelist, -codelist[i])
   append!(color, [color[i]])
  end
 end
 codelist[codelist .== -15] .= 48
 codelist[codelist .== -28] .= 49
 codelist[codelist .== -47] .= 50
 lon = []
 lat = []
 for i in codelist
  fn = @sprintf "jpn/%02i" i
  xy = parse.(Int, split(readline(fn)));
  append!(lon, vcat(xy[1:2:end], 0))
  append!(lat, vcat(xy[2:2:end], 0))
 end
 minlon = minimum(lon[lon .!= 0])
 maxlat = maximum(lat[lat .!= 0])
 lon = map(x -> x == 0 ? 0 : x - minlon + 1, lon)
 lat = map(x -> x == 0 ? 0 : maxlat - x + 1, lat)
 map0(DataFrame(lon=lon, lat=lat); color)
end

function rgb(cn::Int) # 各色 5 段階
 colorset = [
  ["#ffffff", "#bfbfbf", "#7f7f7f", "#151515", "#000000"],  # 灰色1  cn = 1
  ["#eeeeee", "#bbbbbb", "#999999", "#777777", "#555555"],  # 灰色2  cn = 2
  ["#ee0000", "#bb0000", "#990000", "#770000", "#550000"],  # 赤色系 cn = 3
  ["#00ee00", "#00bb00", "#009900", "#007700", "#005500"],  # 緑色系 cn = 4
  ["#0000ee", "#0000bb", "#000099", "#000077", "#000055"],  # 青色系 cn = 5
  ["#ee00ee", "#bb00bb", "#990099", "#770077", "#550055"],  # 紫色系 cn = 6
  ["#00eeee", "#00bbbb", "#009999", "#007777", "#005555"],  # 水色系 cn = 7
  ["#eeee00", "#bbbb00", "#999900", "#777700", "#555500"]]  # 黄色系 cn = 8
 [rgb(i) for i in colorset[cn]]
end

function rgb(str::String) # 任意の "#aabbcc"
 r, g, b = [parse(Int, str[i:i+1], base=16)/256 for i =2:2:6]
 RGB(r, g, b)
end

function colormap1(x; colornumber=8) # モノクロ・デフォルト色で既定の段階で描画
 colornumber in 1:8 || error("color.no は，1〜8 の整数でなければなりません")
 divideat = [9, 19, 28, 38];
 xs = sort(x);
 divideat2 = (xs[divideat] .+ xs[divideat .+ 1]) ./ 2;
 rank = [sum(z .> divideat2) + 1 for z in x];
 colormap(collect(1:47), color=rgb(colornumber)[rank])
end

function colormap2(x, t; colornumber=8) # モノクロ・デフォルト色で任意の段階で色分け
 length(t) == 4 || error("t = $t は，長さ4のベクトルでなければなりません")
 colornumber in 1:8 || error("color.no = $colornumber は，1〜8 の整数でなければなりません")
 rank = [sum(z .>= t) + 1 for z in x];
 colormap(collect(1:47), color=rgb(colornumber)[rank])
end

function colormap3(x, t, colorset) # 任意の段階数，任意の色で塗り分け
 length(t)+1 == length(colorset) || error("t の長さ ($(length(t))) は colorset の長さ ($(length(colorset))) より 1 だけ小さくなければならない")
 rank = [sum(z .>= t) + 1 for z in x];
 colormap(collect(1:47); color=colorset[rank])
end

function colormap4(prefs, marks, color, others = :white) # 複数の県の一部だけ塗り分け
 colormap(prefs, color=map(x -> x in marks ? color : others, prefs))
end

# colormap

color = [RGB(i, 0, 0) for i = 0.2:1/5:1];
colormap(collect(1:47), color=rand(color, 47));

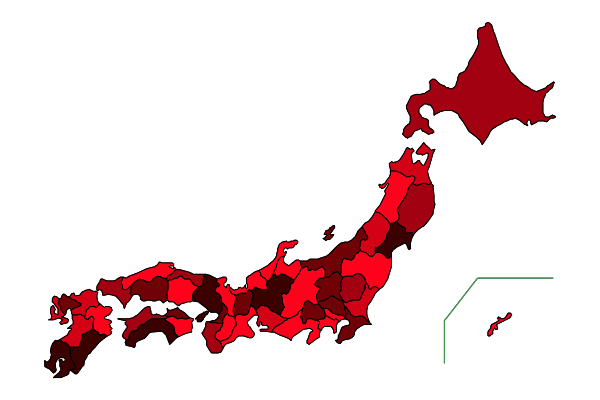
codelist = vcat(collect(8:15), 19, 20);
colormap(codelist, color=rand(color, length(codelist)))

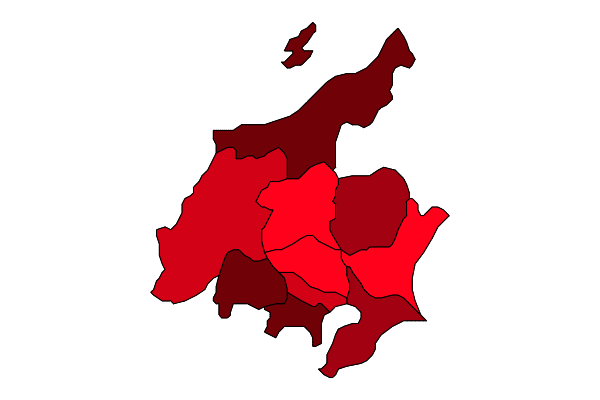
# colormap1

x = rand(47);
colormap1(x; colornumber=8)

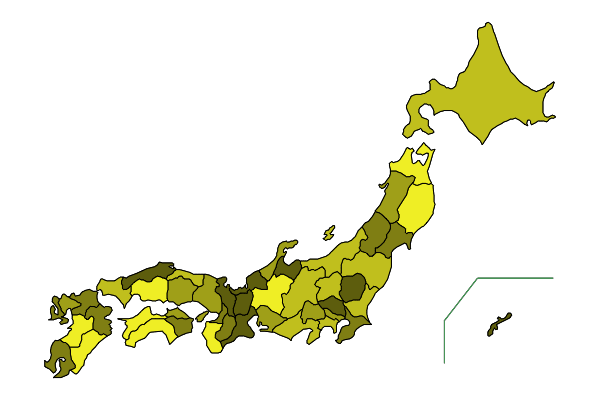
# colormap2

t = [0.2, 0.5, 0.8, 1]; # 任意の段階
colormap2(x, t, colornumber=4)

# colormap3

funky = [:red, :blue, :yellow, :green, :cyan, :magenta, :black];
t = collect(0.1:0.15:0.85);
colormap3(rand(47), t, funky)

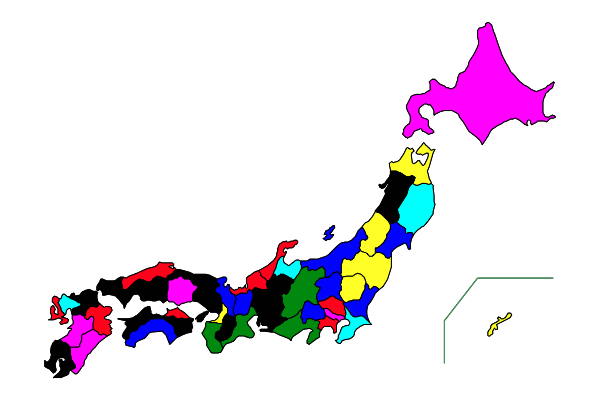
# colormap4

prefs = vcat(collect(7:15), 19, 20);
marks = [10, 13];
colormap4(prefs, marks, RGB(0.4, 0.6, 0.8), RGB(0.85, 0.93, 0.95))

Julia の小ネタ--003

ファイルからベクトルに読み込むプログラム

一行に 2 個の整数をタブで区切って入力しているファイルがある。
1 2
3 4
5 6
 :

これを，nx2 の行列に読み込むとき，str へ readline() で読み込んで，なまじ「改行文字は \r」と思っていたので，split(str, "\r") のようにしたら，最後の行で
input string is empty or only contains whitespace
となってしまった。split(str) だけでよかったのだ。

その後も，reshape() しようかそれとも別の方法にしようかと悩んだが，
結局 x = intxy[1:2:end]，y = intxy[2:2:end] のほうがわかりやすいか？と思った次第。

f = open("jpn/13", "r")
str = readline(f);
close(f)
strxy = split(str);
intxy = parse.(Int, strxy);
x = intxy[1:2:end]
y = intxy[2:2:end]

最初の 3 行を 1 行で書いてもよいが，ちょっとお行儀が悪いかな？

str = readline("jpn/13")
strxy = split(str);
intxy = parse.(Int, strxy);
x = intxy[1:2:end]
y = intxy[2:2:end]

 

Julia の小ネタ-002

変数の書式付き出力

Julia の println() で，出力文字列中に「$変数名」を記述すれば，その場所に変数の値が出力されるのは，よく知られている。Python では 「{変数名}」 とするやつだ。

x = sqrt(2)
println("x = $x") # x = 1.4142135623730951

しかし，これだと小数点以下が長すぎるとか，困ることもある。

そこで，Printf パッケージの @printf()，@sprintf() を使えば C や Python のような % 書式を使うことができる。

using Printf

@printf("n = %05d, x = %.7g", 11, x) # n = 00011, x = 1.414214

@sprintf "n = %05d" 11               # "n = 00011"
@sprintf "pi = %.7g" pi              # "pi = 3.141593"

Formatting パッケージの format でも @sprintf と同じようなことができるが，g, G 変換がまだサポートされていないので，私としては対象外だ。

using Formatting

format("n = {:05d} pi = {:.7e}", 5, pi) # "n = 00005 pi = 3.1415927e+00"

Julia の小ネタ-001

ベクトルの中から特定の値を持つ要素を除いたベクトルを得る

R でもやる，インプレースではない方法
元のベクトルを変えるなら a に代入。
別の変数に代入すれば a は元のまま。

a = [2, 1, 4, 3, 4, 5]
a = a[a .!= 4]
a　# [2, 1, 3, 5]

以下は全てインプレース。
deleteat!(), filter!() は結果も返すので，別の変数に代入することもできる。
findfirst(), findlast(), findall() の第 1 引数は関数。

該当する要素を全て除いたベクトルを得る。

a = [2, 1, 4, 3, 4, 5]
deleteat!(a, findall(isequal(4), a))
a # [2, 1, 3, 5]

a = [2, 1, 4, 3, 4, 5]
filter!(x -> x != 4, a) # λ関数（無名関数）
a # [2, 1, 3, 5]

a = [2, 1, 4, 3, 4, 5]
filter!(!=(4), a) # != も関数
a # [2, 1, 3, 5]

a = [2, 1, 4, 3, 4, 5]
filter!(!isequal(4), a) # 関数はいくつか用意されている。
a # [2, 1, 3, 5]

該当する最初の要素だけを除く場合。

a = [2, 1, 4, 3, 4, 5]
deleteat!(a, findfirst(isequal(4), a))
a # [2, 1, 3, 4, 5]

該当する最後の要素だけを除く場合。

a = [2, 1, 4, 3, 4, 5]
deleteat!(a, findlast(isequal(4), a))
a # [2, 1, 4, 3, 5]

問題

整数ベクトル x の中に 5 が 3 個以上あるのは確かである。
2番目に出てくる 5 だけを削除したベクトルを求めなさい。

例

x = [3, 5, 2, 4, 6, 5, 8, 4, 5] のとき，[3, 5, 2, 4, 6, 8, 4, 5] を求める。

例解

x = [3, 5, 2, 4, 6, 5, 8, 4, 5]
deleteat!(x, findall(isequal(5), x)[2])

Julia に翻訳--001

#=
Julia の修行をするときに，いろいろなプログラムを書き換えるのは有効な方法だ。
以下のプログラムを Julia に翻訳してみる。

日本地図を描く（白地図のみ）
http://aoki2.si.gunma-u.ac.jp/R/map.html

draw.map <- function(fn) # 境界線データのあるファイル名
{
        data <-read.table(fn, header=FALSE) # x, y 座標が組みになっている
        data[data[,1]==0 & data[,2]==0,] <- NA # x, y 座標が共に 0 であるのは，一連の境界線の終わりを意味する
        plot(data, type = "l", axes=FALSE, bty="n", xlab="", ylab="", asp=1) # (NA, NA) は，結線されない
}

ファイル名: drawmap.jl　　関数名: drawmap

翻訳するときに書いたメモ

• 列名のないファイルをデータフレームに読むときは，header=["x", "y"] のように名前を付けて読む。
• 欠損値は missing で表される。
• 元のファイルに欠損値があるときは，欠損値を表す文字列を missingstring="missing" で指定しないと，含まれる列が String 型になってしまう。
• 元のファイルに欠損値がなくて，読み込み後のデータ処理で missing を割り当てる場合は，allowmissing!() で missing を許容するように変換する必要がある。
• 行の選択のときなどで，複数の比較演算結果を論理演算するときは，比較演算は (data.x .== 0) .& (data.y .== 0) のように，( ) でくくること。
• plot される x, y データ中に missing があると，その点は描画されない。これを利用することができる。
• plot 引数で，よく使うもの
  線の色        linecolor=:black
  軸の描画      showaxis=false
  ティックマーク ticks=false
  グリッド      grid=false
  線の凡例      label=""
  アスペクト比   aspect_ratio=1

=#

using Plots, CSV, DataFrames
function drawmap(fn)
        data = CSV.read(fn, DataFrame, header=["x", "y"])
        allowmissing!(data)
        data[(data.x .== 0) .& (data.y .== 0), :] .= missing
        plot(data.x, data.y, linecolor=:black, showaxis=false,
             ticks=false, grid=false, label="", aspect_ratio=1)
end

drawmap("jpn.dat")
drawmap("map.data/toukyou")

逆引き辞書 Python, R, Julia （その 4）

メッシュグリッド

# Python
a, b = np.meshgrid([1,2,3], [4, 5, 6, 7])
a
# array([[1, 2, 3],
#        [1, 2, 3],
#        [1, 2, 3],
#        [1, 2, 3]])
b
# array([[4, 4, 4],
#        [5, 5, 5],
#        [6, 6, 6],
#        [7, 7, 7]])

# R
x = matrix(0, 4, 3)

col(x) # 列番号を要素とする行列
#      [,1] [,2] [,3]
# [1,]    1    2    3
# [2,]    1    2    3
# [3,]    1    2    3
# [4,]    1    2    3
#
row(x) # 行番号を要素とする行列
#  [,1] [,2] [,3]
# [1,]    1    1    1
# [2,]    2    2    2
# [3,]    3    3    3
# [4,]    4    4    4
#
row(x)+3 # 加工すればよい
#      [,1] [,2] [,3]
# [1,]    4    4    4
# [2,]    5    5    5
# [3,]    6    6    6
# [4,]    7    7    7

# Julia
function meshgrid(x, y)
    nr = length(y)
    nc = length(x)
    transpose(reshape(repeat(x, nr), nc, :)), reshape(repeat(y, nr), nr, :)
end

a, b = meshgrid([1,2,3], [4, 5, 6, 7])
# a : [1 2 3; 1 2 3; 1 2 3; 1 2 3]
# b : [4 4 4 4; 5 5 5 5; 6 6 6 6; 7 7 7 7]

配列の連結

# Python
a = np.array([1.0, 2.0, 3.0])           # [ 1.  2.  3.]
b = np.array([5.0, 6.0, 7.0])           # [ 5.  6.  7.]
np.vstack((a, b))                       # [[ 1.,  2.,  3.], # np でも同じ
                                        #  [ 5.,  6.,  7.]]
np.hstack((a, b))                       # [ 1.,  2.,  3.,  5.,  6.,  7.]
#
x = np.array([[1, 2, 3], [4, 5, 6]])
y = np.array([[10, 11, 12], [20, 21, 22]])

np.vstack((x, y))                       # [[ 1,  2,  3], # rbind
                                        #  [ 4,  5,  6],
                                        #  [10, 11, 12],
                                        #  [20, 21, 22]]

np.hstack((x, y))                       # [[ 1,  2,  3, 10, 11, 12], # cbind
                                        #  [ 4,  5,  6, 20, 21, 22]]
#
np.concatenate((a, b))                  # [ 1.,  2.,  3.,  5.,  6.,  7.]

np.concatenate(([a], [b]))              # [[ 1.,  2.,  3.],
                                        #  [ 5.,  6.,  7.]]
#
np.concatenate((x, y), axis=0)  # [[ 1,  2,  3],
                                        #  [ 4,  5,  6],
                                        #  [10, 11, 12],
                                        #  [20, 21, 22]]

np.concatenate((x, y), axis=1)  # [[ 1,  2,  3, 10, 11, 12],
                                        #  [ 4,  5,  6, 20, 21, 22]]
#
np.c_[a, b]                             # [[ 1.,  5.],              R: cbind()
                                        #  [ 2.,  6.],
                                        #  [ 3.,  7.]]

np.r_[a, b]                             # [ 1.,  2.,  3.,  5.,  6.,  7.]     R: rbind()
#
np.c_[x, y]                             # [[ 1,  2,  3, 10, 11, 12],
                                        #  [ 4,  5,  6, 20, 21, 22]]

np.r_[x, y]                             # [[ 1,  2,  3],
                                        #  [ 4,  5,  6],
                                        #  [10, 11, 12],
                                        #  [20, 21, 22]]

# R
a = c(1, 2, 3)
b = c(5, 6, 7)
x = matrix(1:6, ncol=3, byrow=TRUE)
y = matrix(c(10, 11, 12, 20, 21, 22), ncol=3, byrow=TRUE)

rbind(a, b)
cbind(a, b) # np.c_ に相当
c(a, b)
append(a, b)

rbind(x, y)
cbind(x, y)

# Julia
a = [1, 2, 3]
b = [5, 6, 7]
x = [1 2 3; 4 5 6]
y = [10 11 12; 20 21 22]

vcat(a, b) # [1, 2, 3, 4, 5, 6]
hcat(a, b) # [1 5; 2 6; 3 7]

vcat(x, y)
# 1   2   3
# 4   5   6
# 10  11  12
# 20  21  22

hcat(x, y)
# 1  2  3  10  11  12
# 4  5  6  20  21  22

逆引き辞書 Python, R, Julia （その 3）

次元数の変更

# Python
a = np.reshape(np.arange(9), (3, 3)) # array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
b = np.reshape(np.arange(9), (3, -1))
c = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
d = np.reshape(c, (9,))              # array([0, 1, 2, 3, 4, 5, 6, 7, 8])

# Julia
vec1 = collect(1:6);   # [1, 2, 3, 4, 5, 6]
reshape(vec1, 2, 3);   # [1 3 5; 2 4 6]　# 2x3 行列
reshape(vec1, (2, 3)); # [1 3 5; 2 4 6]　# 2x3 行列
reshape(vec1, 2, :);   # [1 3 5; 2 4 6]  # 2x3 行列
reshape(vec1, 6, :);   # 6x1 行列

リサイズ（インプレースで変更）

# Python
d = np.arange(4); d.resize((6,)); d # [0, 1, 2, 3, 0, 0]
a = np.array([[1, 2, 3], [4, 5, 6]])
a.resize((6,))                      # [1, 2, 3, 4, 5, 6]; 行列からベクトル
#
e = np.arange(4)
e.resize((4, 2)) # [[0, 1], [2, 3], [0, 0], [0, 0]] # ベクトルから行列

行列をベクトルに変更，スカラーさえも

# Python
x = np.array([[1,2,3,4],[5,6,7,8]]); np.ravel(x)
np.ravel(1) # [1]

# R
x = matrix(1:8, byrow=TRUE, ncol=4)
c(t(x)) # 列優先
c(x)    # 行優先なら c(x)

# Julia
x = [1 2 3 4; 5 6 7 8]
vec(x') # [1, 2, 3, 4, 5, 6, 7, 8]
vec(x)  # [1, 5, 2, 6, 3, 7, 4, 8]

a = 1
[a]

単位行列

# Python
np.identity(3)
np.eye(3)
np.eye(3, 5) # 3x5 行列

# R
diag(3)

# Julia
using LinearAlgebra
Array{Int}(I, 3, 3)　   # 3x3 行列
Array{Float64}(I, 3, 3)
Array{Float64}(I, 2, 3) # 2x3 行列

対角行列

# Python
np.diag([1, 3, 9])

# R
diag(c(1, 3, 9)) # 対角要素が c(1, 3, 9)
diag(3, 5)       # 対角要素が 3 の 5x5 行列

# Julia
diagm(0 => 1:3)
diagm(0 => [1, 3, 9])
diagm(1 => [1, 3, 9])                   # 対角要素の 1 つ上。従って 4x4 行列
diagm(-2 => [1, 3, 9])                  # 対角要素の 2 つ下。従って 5x5 行列
diagm(1 => [1, 3, 9], -2 => [2, 6, 13]) # 複数指定も可
Diagonal([1, 2, 3])
Diagonal(ones(3))
Diagonal(ones(Int, 3))

対角成分へ代入

# Python
r = np.reshape(np.arange(1, 10), (3, 3))
diag2 = np.eye(3) == 1
r[diag2] = 999 # [[999, 2, 3], [4, 999, 6], [7, 8, 999]]

# R
r = matrix(1:9, byrow=TRUE, 3)
diag(r) = 999

Julia には用意されていないようなので，独自関数を定義する。

function diag!(a, b)
    [a[i, i] = b[i] for i=1:length(b)]
end

a = [1 2 3; 4 5 6; 7 8 9]
b = [10 20 30]

diag!(a, b)
a

対角成分の取り出し

# Python
r = np.reshape(np.arange(1, 10), (3, 3))
np.diag(r)      # [1, 5, 9]
np.diag(r, 1)   # [2, 6] 対角線の 1 つ上
np.diag(r, -2)  # [7] 対角線の 2 つ下

# R
r = matrix(1:9, byrow=TRUE, 3)
diag(r)         # c(1, 5, 9)

# Julia
r = [1 2 3; 4 5 6; 7 8 9]
diag(r)         # [1, 5, 9]
diag(r, 1)      # [2, 6]
diag(r, -2)     # [7]

三角行列

要素が 1 の下三角行列の作成

# Python
np.tri(3)
np.tri(2, 5, 2)
np.tri(3, 5, -1)

# R
a = matrix(0, 3, 3)
a[lower.tri(a, diag=TRUE)] = 1 # np.tri(n) に相応

下三角行列（上三角行列）の抽出

# Python
a = np.reshape(np.arange(1, 10), (3,3))
# array([[1, 2, 3],
#        [4, 5, 6],
#        [7, 8, 9]])
np.tril(a)
# array([[1, 0, 0],
#        [4, 5, 0],
#        [7, 8, 9]])
np.tril(a, -1)         # 対角成分より一つ下（対角を含まない）
# array([[0, 0, 0],
#        [4, 0, 0],
#        [7, 8, 0]])
np.triu(a)
# array([[1, 2, 3],
#        [0, 5, 6],
#        [0, 0, 9]])
np.triu(a, -1)         # 対角成分より一つ下（対角を含まない）
# array([[1, 2, 3],
#        [4, 5, 6],
#        [0, 8, 9]])

# R
ifelse(lower.tri(a, diag=TRUE), a, 0)
ifelse(lower.tri(a), a, 0)            # 対角成分より一つ下
ifelse(upper.tri(a, diag=TRUE), a, 0)
ifelse(upper.tri(a), a, 0)            # 対角成分より一つ上

# Julia
a = [1 2 3; 4 5 6; 7 8 9]
[i <= j ? a[j, i] : 0 for j = 1:n, i = 1:n] # 不等式部分でどこから取り出すかを指定
[i < j ? a[j, i] : 0 for j = 1:n, i = 1:n]
[i >= j ? a[j, i] : 0 for j = 1:n, i = 1:n]
[i >= j-1 ? a[j, i] : 0 for j = 1:n, i = 1:n]

下三角行列の要素をベクトルとして抽出

# Python
a = np.reshape(np.arange(1, 10), (3,3))
# array([[1, 2, 3],
#        [4, 5, 6],
#        [7, 8, 9]])
#
b = np.tril(np.ones_like(a)) > 0
# array([[ True, False, False],
#        [ True,  True, False],
#        [ True,  True,  True]])
a[b]    # [1, 4, 5, 7, 8, 9]
#
b2 = np.triu(np.ones_like(a)) > 0
# array([[ True,  True,  True],
#        [False,  True,  True],
#        [False, False,  True]])
a[b2]    # [1, 2, 3, 5, 6, 9]
#
c = np.tril(np.ones_like(a), -1) > 0
# array([[False, False, False],
#        [ True, False, False],
#        [ True,  True, False]])
a[c]    # [4, 7, 8]
#
c2 = np.triu(np.ones_like(a), -1) > 0
# array([[ True,  True,  True],
#        [ True,  True,  True],
#        [False,  True,  True]])
a[c2]    # array([1, 2, 3, 4, 5, 6, 8, 9])

# R
a = matrix(1:9, 3, byrow=TRUE)
#
a[lower.tri(a, diag=TRUE)] # c(1, 4, 7, 5, 8, 9); 列優先になる
a[upper.tri(a, diag=TRUE)] # c(1, 2, 5, 3, 6, 9)
#
a[lower.tri(a)] # c(4, 7, 8)
a[upper.tri(a)] # c(2, 3, 6)

# Julia
a = [1 2 3; 4 5 6; 7 8 9]
using LinearAlgebra
a[tril(trues(size(a)))] # [1, 4, 7, 5, 8, 9]; 列優先になる
a[triu(trues(size(a)))] # [1, 2, 5, 3, 6, 9]

下三角行列（上三角行列）への代入

# Python
r = np.reshape(np.arange(1, 10), (3, 3))
# array([[1, 2, 3],
#        [4, 5, 6],
#        [7, 8, 9]])
p = 100 * r
# array([[100, 200, 300],
#        [400, 500, 600],
#        [700, 800, 900]])
lower = np.tri(3) == 1
r[lower] = p[lower]
print(r)
# array([[100,   2,   3],
#        [400, 500,   6],
#        [700, 800, 900]])

# R
r = matrix(1:9, 3, byrow=TRUE)
#      [,1] [,2] [,3]
# [1,]    1    2    3
# [2,]    4    5    6
# [3,]    7    8    9
p = 100 * r
#      [,1] [,2] [,3]
# [1,]  100  200  300
# [2,]  400  500  600
# [3,]  700  800  900
ifelse(lower.tri(p, diag=TRUE), p, r)
#      [,1] [,2] [,3]
# [1,]  100    2    3
# [2,]  400  500    6
# [3,]  700  800  900
ifelse(upper.tri(p, diag=TRUE), p, r)
#      [,1] [,2] [,3]
# [1,]  100  200  300
# [2,]    4  500  600
# [3,]    7    8  900

# Julia
r = [1 2 3; 4 5 6; 7 8 9]
# 1  2  3
# 4  5  6
# 7  8  9
p = 100 * r
# 100  200  300
# 400  500  600
# 700  800  900
n = size(p, 1)
[i > j ? r[i, j] : p[i, j] for j = 1:n, i = 1:n]
# 100    4    7
# 200  500    8
# 300  600  900
[i < j ? r[i, j] : p[i, j] for j = 1:n, i = 1:n]
# 100  400  700
#   2  500  800
#   3    6  900

 

逆引き辞書 Python, R, Julia （その 2）

初期化した配列（ベクトル，行列）

ゼロベクトル

# Python
np.zeros(3)

# R
integer(3)
numeric(3)
logical(3)

# Julia
zeros(3)       # [0.0, 0.0, 0.0]
zeros(Int, 3)  # [0, 0, 0]
zeros(Bool, 3) # [0 0 0]
falses(3)      # [0 0 0]

ゼロマトリックス

# Python
np.zeros((3, 4))

# R
matrix(0, 3, 4)

# Julia
zeros(3, 4)         # [0.0 0.0 0.0; 0.0 0.0 0.0; 0.0 0.0 0.0]
zeros(Int, 3, 4)    # [0 0 0; 0 0 0; 0 0 0]
zeros(Bool, 3, 4)   # [0 0 0; 0 0 0; 0 0 0]

1 ベクトル

# Python
np.ones(3)

# R
rep(1, 3)

# Julia
ones(3)         # [1.0, 1.0, 1.0]
ones(Int, 3)    # [1, 1, 1]
ones(Bool, 3)   # [1, 1, 1]
trues(3)        # [1, 1, 1]

1 マトリックス

# Python
np.ones((3, 4))

# R
matrix(1, 3, 4)

# Julia
ones(3, 4)      # [1.0 1.0 1.0; 1.0 1.0 1.0; 1.0 1.0 1.0]
ones(Int, 3, 4) # [1 1 1; 1 1 1; 1 1 1]

一定値で初期化するベクトル

# Python
np.repeat(123, 3)
np.full(3, 123)

# R
rep(123, 3)

# Julia
fill(123, 3) # [123, 123, 123]

一定値で初期化するマトリックス

# Python
np.array([[123]*4 for i in range(3)])
np.full((3, 4), 123)

# R
matrix(123, 3, 4)

# Julia
fill(123, 3, 4) # [123 123 123 123; 123 123 123 123; 123 123 123 123]

初期化しないベクトル，行列

# Python
np.empty(5)
np.empty(5, 7)

# Julia
V = Array{Float64, 1}(undef, 5)     # 型の指定は Int64, Int, Bool など
A = Array{Float64, 2}(undef, 5, 7)

既存のベクトル，行列と同じサイズのベクトル，行列

# Python
a = np.ones(5)
np.ones_like(a)
np.zeros_like(a)
np.empty_like(a)
#
b = np.ones((2, 3))
np.ones_like(b)
np.zeros_like(b)
np.empty_like(b)

# Julia
a = ones(5)
a2 = similar(a) # サイズだけが同じで初期化されていないベクトル
b = zeros(2, 3)
b2 = similar(b) # サイズだけが同じで初期化されていない行列

ソート

# Python
a = [4, 1, 3, 5, 2]
sorted(a)
sorted(a, reverse=True)
#
a.sort()
a.sort(reverse=True)   # インプレースでソート
#
b = np.array([[4, 3, 5], [3, 2, 1]])
b.sort(axis=1)         # インプレース・次元指定でソート
#
c = np.sort(b, axis=1) # np.sort はインプレースではない

# R
a = c(4, 1, 3, 5, 2)
sort(a)
sort(a, decreasing=TRUE)
#
x = matrix(c(4, 3, 5, 3, 2, 1), byrow=TRUE, ncol=3)
t(apply(x, 1, sort))  # 次元指定でソート

# Julia
a = [4, 1, 3, 5, 2];
sort(a)
sort(a, rev=true)
#
sort!(a) # インプレースでソート
sort!(a, rev=true) # インプレースで逆順ソート

逆転

# Python
a = [4, 1, 3, 2, 5]
a.reverse()
a[::-1]
#
reversed(a) # 逆順のイテレータ

# R
a = c(4, 1, 3, 2, 5)
rev(a)
a[seq(length(a), 1, by=-1)]

# Julia
a = [4, 1, 3, 2, 5]
reverse(a)      # [5, 2, 3, 1, 4]
a[end:-1:begin] # [5, 2, 3, 1, 4]

小さい順の要素のインデックス

x[o] とすると x がソートされるような o

# Python
x = np.array([2, 1, 2, 3, 4, 5, 4, 3, 4, 6])
o = x.argsort() # array([1, 0, 2, 3, 7, 4, 6, 8, 5, 9]) # 0 から始まる
x[o]            # array([1, 2, 2, 3, 3, 4, 4, 4, 5, 6])
(-x).argsort()  # array([9, 5, 4, 6, 8, 3, 7, 0, 2, 1])

# R
x = c(2, 1, 2, 3, 4, 5, 4, 3, 4, 6)
o = order(x)                           # c(2, 1, 3, 4, 8, 5, 7, 9, 6, 10) # 1 から始まる
x[o] = c(1, 2, 2, 3, 3, 4, 4, 4, 5, 6)
order(x, decreasing=TRUE)              # c(10, 6, 5, 7, 9, 4, 8, 1, 3, 2)

# Julia
x = [2, 1, 2, 3, 4, 5, 4, 3, 4, 6]
o = sortperm(x) # [2, 1, 3, 4, 8, 5, 7, 9, 6, 10]
x[o]            # [1, 2, 2, 3, 3, 4, 4, 4, 5, 6]

逆順ソートに対応するベクトル ro を返す。
ro = sortperm(x, rev=true) # [10, 6, 5, 7, 9, 4, 8, 1, 3, 2]
x[ro] # [6, 5, 4, 4, 4, 3, 3, 2, 2, 1]

等差数列

公差=1

# Python
list(range(5))
np.array(range(5))
np.arange(5)

# R
0:4
seq(0, 4)

# Julia
Vector(0:4)                     # [0, 1, 2, 3, 4]
collect(0:4)                    # [0, 1, 2, 3, 4]
range(0, 4, step=1)             # 0:1:4 # イテレータ
collect(range(0, 4, step=1))    # [0, 1, 2, 3, 4]

公差≠1

# Python
np.arange(10, 13, 0.5) # array([10., 10.5, 11., 11.5, 12., 12.5])

# R
seq(10, 12.5, 0.5)     # c(10, 10.5, 11, 11.5, 12, 12.5)

# Julia
Vector(10:0.5:12.5)                 # [10.0, 10.5, 11.0, 11.5, 12.0, 12.5]
collect(10:0.5:12.5)                # [10.0, 10.5, 11.0, 11.5, 12.0, 12.5]
range(10, 12.5, step=0.5)           # 10.0:0.5:12.5 # イテレータ
collect(range(10, 12.5, step=0.5))  # [10.0, 10.5, 11.0, 11.5, 12.0, 12.5]

長さ指定

# Python
np.linspace(1, 6, 5) # [1., 2.25, 3.5, 4.75, 6.]

# R
seq(1, 6, length=5)  # c(1, 2.25, 3.5, 4.75, 6)

# Julia
collect(1:(6-1)/4:6)            # [1.0, 2.25, 3.5, 4.75, 6.0]
range(1, 6, length=5)           # 1.0:1.25:6.0 # イテレータ
collect(range(1, 6, length=5))  # [1.0, 2.25, 3.5, 4.75, 6.0]

等比数列

# Python
np.logspace(0, 2, num = 3, dtype=int) # array([1, 10, 100]) i.e. 10^0, 10^1, 10^2
np.logspace(0, 5, num = 6, base=3)    # array([1., 3., 9., 27., 81., 243.])

# R
10^(0:2) # c(1, 10, 100)
3^(0:5)  # c(1, 3, 9, 27, 81, 243)

10 .^ (0:2) # [1, 10, 100]
3 .^ (0:5)  # [1, 3, 9, 27, 81, 243]

乱数

乱数の種

# Python
import random
random.seed(123)
#
np.random.seed(123)

# R
set.seed(123)

# Julia
using Random
Random.seed!(123)

一様乱数

# Python
random.random()                  # [0, 1) の一様乱数を 1 個
random.uniform(min, max)         # [min, max) の一様乱数
random.randint(min, max)         # [min, max] の整数一様乱数
np.random.rand(n)                # [0, 1) の一様乱数を n 個
np.random.randint(min, max, n)   # [min, max) の整数一様乱数を n 個

# R
runif(n, min, max)               # [min, max) の一様乱数を n 個
sample(min:max, n, replace=TRUE) # [min, max] の整数一様乱数 を n 個
sample(max, n, replace=TRUE)     # [1, max] の整数一様乱数 を n 個

# Julia
rand(n)         # Float64 の [0, 1) の一様乱数
rand(Int8, n)   # Int8 の一様乱数を n 個
rand(Int32, n)  # Int32 の一様乱数を n 個

無作為抽出

# Python
random.randint(min, max)            # [min, max] の整数一様乱数 1 個
np.random.randint(min, max, n)      # [min, max) の整数一様乱数 n 個
np.random.sample(["A", "B", "C"], n, replace=True)

# R
sample(min:max, n, replace=TRUE)    # [min, max] の整数一様乱数 n 個
sample(c("A", "B", "C"), n, replace=TRUE)

# Julia
n = 3; min0=1; max0=6
rand(min0:max0, n)                  # min0:max0 から n 個を無作為抽出
rand(["A", "B", "C"], n)            # ベクトル要素を無作為抽出
rand(('x', 'y', :z), n)             # ベクトル要素を無作為抽出
rand(2, 3)                          # 2x3 の一様乱数行列

ベクトルをシャッフル（重複なしの無作為抽出）

# Python
np.shuffle(x)

# R
sample(x)

# Julia
x = collect(1:10)
shuffle(x)

正規乱数

# Python
random.normalvariate(mean, std)     # 平均値 = mean, 標準偏差 = std の正規乱数 1 個
random.gauss(mean, std)             # 平均値 = mean, 標準偏差 = std の正規乱数 1 個
np.random.normal(mean, std, n)      # 平均値 = mean, 標準偏差 = std の正規乱数 n 個
np.random.normal(mean, std, (n, m)) # nxm の正規乱数行列

# R
rnorm(n, mean, sd)                  # 平均値 = mean, 標準偏差 = sd の正規乱数 n 個
matrix(rnorm(n*m, mean, sd), n, m)  # nxm の正規乱数行列

# Julia
Random.seed!(123)
randn(3)                            # 長さ 3 の正規乱数ベクトル（平均値 = 0，標準偏差 = 1 に固定）
randn(3, 4)                         # 3x4 の正規乱数行列

逆引き辞書 Python, R, Julia （その 1）

in 演算子

# Python
a = range(1, 11)
3 in range(1, 11) # True
3 in a            # True
not(3 in a)       # False
20 not in a       # True

# R
a = 1:10
3 %in% a        # TRUE
!(3 %in% a)     # FALSE
20 %in% a       # FALSE

# Julia
a = 1:10        # 1:10
b = collect(a)  # [1, 2, ..., 9, 10]
typeof(a)       # UnitRange{Int64}
typeof(b)       # Array{Int64,1}
3 in a          # true
3 in b          # true
!(3 in a)       # false
20 in a         # false

どこにあるか

# Python
a = [3, 1, 0, 2, 4, 0, 3, 5, 4, 2]
a.index(4)                 # 4
#
b = np.array([3, 2, 1, 2, 3, 4, 1])
c = np.where(b == 1)       # (array([2, 6]),)
c[0]                       # array([2, 6])
c[0][0]                    # 2
c[0][1]                    # 6

# R
a = c(3, 1, 0, 2, 4, 0, 3, 5, 4, 2)
which(a == 4)               # 5, 9

# Julia
a = [3, 1, 0, 2, 4, 0, 3, 5, 4, 2]
findfirst(==(4), a)         # 5
findfirst(isequal(4), a)    # 5
#
findfirst(>(3), a)          # 5
findall(iseven, a)          # [3, 4, 5, 6, 9, 10]
findall(isodd, a)           # [1, 2, 7, 8]
#
findfirst(==(3), a)         # 1
findlast(==(3), a)          # 7
findall(==(3), a)           # [1, 7]

いくつあるか

# Python
a = [3, 1, 0, 2, 4, 0, 3, 5, 4, 2]
a.count(3)                  # 2

# R
a = c(3, 1, 0, 2, 4, 0, 3, 5, 4, 2)
length(which(a == 3))       # 2

# Julia
a = [3, 1, 0, 2, 4, 0, 3, 5, 4, 2]
count(==(3), a)             # 2
count(isequal(3), a)        # 2

三項演算子

# Python
i = 6
a = "even" if i % 2 == 0 else "odd"     # 'even'

# R
i = 6
a = if (i %% 2 == 0) "even" else "odd"  # "even"

# Julia
i = 6
a = i % 2 == 0 ? "even" : "odd"         # "even"

条件により実行される演算を選択する

# Python
import numpy as np
a = np.array([2, 3, 5, 6, 8])
b = np.where(a % 2 == 0, a*10, 0)     # array([20,  0,  0, 60, 80])

# R
a = c(2, 3, 5, 6, 8)
b = ifelse(a %% 2 == 0, a*10, 0)      # c(20, 0, 0, 60, 80)

# Julia
a = [2, 3, 5, 6, 8];
b = map(x -> x % 2 == 0 ? 10x : 0, a) # [20, 0, 0, 60, 80]

リスト（配列）同士の連結

# Python
a = [1, 2, 3]
b = [11, 12]
x = a + b           # [1, 2, 3, 11, 12]; インプレースではない
#
import operator as op
y = op.concat(a, b) # [1, 2, 3, 11, 12]
#
a.extend(b)         # [1, 2, 3, 11, 12]; a にインプレースで連結
#
a2 = np.array([1, 2, 3])
b2 = np.array([11, 12])
x = np.hstack((a2, b2)) # array([1, 2, 3, 11, 12]); インプレースではない

# R
a = c(1, 2, 3)
b = c(11, 12)
x = c(a, b)         # c(1, 2, 3, 11, 12); インプレースではない
y = append(a, b)    # c(1, 2, 3, 11, 12); インプレースではない

# Julia
a = [1, 2, 3];
b = [11, 12];
x = vcat(a, b)      # [1, 2, 3, 11, 12]; インプレースではない
append!(a, b)       # [1, 2, 3, 11, 12]; a にインプレースで連結

リストに変数を連結

# Python
a = [1, 2, 3]
b = 5
x = a + [b]         # [1, 2, 3, 5]; インプレースではない
a.append(b)         # [1, 2, 3, 5]; a にインプレースで連結
#
a2 = np.array([1, 2, 3])
b = 5
x = np.hstack((a2, b)) # [1, 2, 3, 5]; インプレースではない

# R
a = c(1, 2, 3)
b = 5
x = c(a, b)         # c(1, 2, 3, 5); インプレースではない
y = append(a, b)    # c(1, 2, 3, 5); インプレースではない

# Julia
a = [1, 2, 3]
b = 5
x = vcat(a, b)      # [1, 2, 3, 5]; インプレースではない
append!(a, b)       # [1, 2, 3, 5]; a にインプレースで追加

リストに変数を挿入

# Python
a = [1, 2, 3]
b = 5
a.insert(0, b)      # [5, 1, 2, 3]; a にインプレースで挿入

# R
a = c(1, 2, 3)
b = 5
x = append(a, b, 0) # c(5, 1, 2, 3); インプレースではない

# Julia
a = [1, 2, 3]
b = 5
insert!(a, 1, b)    # [5, 1, 2, 3]; a にインプレースで挿入

要素の全削除

# Python
a = [1, 2, 3]
a.clear()
a                 # []; 要素がなくなるのであって，a 自体がなくなるわけではない

# R
a = c(1, 2, 3)
a = NULL
a                 # NULL; 要素がなくなるのであって，a 自体がなくなるわけではない

# Julia
a = [1, 2, 3]
empty!(a)
a                 # Int64[]; 要素がなくなるのであって，a 自体がなくなるわけではない

要素の削除

# Python
a = [1, 2, 3]
del a[1]          # インデックスを指定して要素を削除
a                 # [1, 3]
#
a = [1, 2, 3]
a.remove(3)       # 指定する値を持つ要素をインプレースで削除
a                 # [1, 2]

# R
a = c(1, 2, 3)
a = a[-2]         # インプレースではないため，結果を反映させるためには代入が必要

# Julia
a = [1, 2, 3];
deleteat!(a, 2)   # a からインプレースで削除
a # [1, 3]

要素のポップ

# Python
a = [3, 2, 1, 4, 3]
a.pop()             # 3; 取り出された要素
a                   # [3, 2, 1, 4]
#
a = [3, 2, 1, 4, 3 ]
a.pop(1)            # 2; 取り出された要素
a                   # [3, 1, 4, 3]

# R 以下の関数では，取り出した要素は把握できない
pop = function(a, i=length(a)) a[-i]
#
a = c(3, 2, 1, 4, 3)
a = pop(a)
a                   # c(3, 2, 1, 4)
#
a = c(3, 2, 1, 4, 3)
a = pop(a, 3)
a                   # c(3, 2, 4, 3)

# Julia
a = [3, 2, 1, 4, 3];
pop!(a)             # 3; 取り出された要素
a                   # [3, 2, 1, 4] # a からインプレースで最後の要素を取り出す
#
a = [3, 2, 1, 4, 3];
popfirst!(a)        # 3; 取り出された要素
a                   # [2, 1, 4, 3] # a からインプレースで最初の要素を取り出す

要素のプッシュ

# Python
a = [3, 2, 1, 4, 3]
a.append(88)        # 最後の要素としてインプレースで付け加える（insert を使ってもよい）
a.insert(3, 99)     # [3, 2, 1, 99, 4, 3, 88]; 3 番目の要素としてインプレースで挿入

# R
a = c(3, 2, 1, 4, 3)
a = append(a, 88)        # インプレースではないので，代入しないと変化なし
a = append(a, 99, 3)     # インプレースではないので，代入しないと変化なし
a                        # c(3, 2, 1, 99, 4, 3, 88)

# Julia
a = [3, 2, 1, 4, 3];
pushfirst!(a, 10)        # a にインプレースで先頭に要素を押し込む
push!(a, 20)             # a にインプレースで最後尾に要素を押し込む
a                        # [10, 3, 2, 1, 4, 3, 20]

リストの繰り返し

# Python
a = [1, 2, 3]
b = a*3                  # [1, 2, 3, 1, 2, 3, 1, 2, 3]
#
np.tile(a, 3)            # array([1, 2, 3, 1, 2, 3, 1, 2, 3])
#
np.repeat(a, 3)          # array([1, 1, 1, 2, 2, 2, 3, 3, 3])
#
np.repeat(np.array([1,2]), [2,3])    # array([1, 1, 2, 2, 2])

# R
rep(c(1, 2, 3), 3)       # c(1, 2, 3, 1, 2, 3, 1, 2, 3)
#
rep(c(1, 2, 3), each=3)  # c(1, 1, 1, 2, 2, 2, 3, 3, 3)
#
rep(c(1, 2), c(2, 3))    # c(1, 1, 2, 2, 2)

# Julia
repeat([1, 2, 3], 3)     # [1, 2, 3, 1, 2, 3, 1, 2, 3]
#
repeat([1 2 3], inner=(1, 2))               # [1 1 2 2 3 3]; 1x6 行列
reshape(repeat([1 2 3], inner=(1,2)), 6, :) # [1, 1, 2, 2, 3, 3]; 6x1 行列
#
# 関数定義
repeateach(x, n) = vec([j for i = 1:n, j in x])
a = repeateach([1, 2, 3], 3)        # [1, 1, 1, 2, 2, 2, 3, 3, 3]
a = repeateach(["a", "b", "c"], 2)　# ["a", "a", "b", "b", "c", "c"]

 

数学問題を解きましたということなんだが

曲線 y = x^3 上に，点 A(-1, -1)，B(1, 1)，P(t, t^3) を置く。ただし，0 < t < 1。
直線 AP と x 軸のなす角を α，直線 PB と x 軸のなす角を β とする。
tan α，tan β を t を用いて表せ。ただし，0 < α < π/2, 0 < β < π/2 とする。
tan∠APB を t を用いて表せ。
tan∠APB を最小にする t の値を求めよ。

using Plots
x = -1.1:0.01:1.1
y = x .^ 3;
p = plot(x, y, xlabel="\$x\$", ylabel="\$y\$", label="",
   xlims=(-1.5, 1.5), ylims=(-1.1, 1.1),
   size=(600, 400), aspect_ratio=1);
x2 = [-1, 0.5, 1];
y2 = x2 .^ 3;
plot!(x2, y2, label="", linecolor=:black);
scatter!(x2, y2, label="", markercolor=:black);
annotate!(-0.65, -1, text("\$A(-1, -1)\$", 10));
annotate!(1.2, 1, text("\$B(1, 1)\$", 10));
annotate!(0.7, 0.4^3, text("\$P(t, t^3)\$", 10));
annotate!(-0.25, 0.15, text("\$y = x^3\$", :blue, 15));
display(p)

例のごとく，詰めが甘い。

問題 1 は，図を描いて，tangent の定義をそのまま書けばよいと。

α = atan((1-t^3)/(1-t))
β = atan((1+t^3)/(1+t))

simplify() してもよいけど...

問題2 は，求める θ を 問題 1 の α，β を用いて表すだけ（ちょっと，混乱するけど）

その後は，手計算でやるんだろうけど，SymPy を使ってずるをする。

using SymPy

@syms θ α β t

# 問題 1
# α = atan((1-t^3)/(1-t))  後に示すように，simplify してもよいけどそのまま
# β = atan((1+t^3)/(1+t))

# 問題 2
θ = π + atan((1-t^3)/(1-t)) - atan((1+t^3)/(1+t))
# 導関数
diff(θ)
# 導関数 = 0 つまり，接線が 0 になるところを求める
solve(diff(θ))
# 以下の内 0 < t < 1 を満たすのは
sqrt(6)/3
# 上のでもよいが，単に数値計算して
0.8164965809277259

# α，βを簡約して，以下のようにも

simplify((t^3+1)/(t+1))
# α = t^2-t+1
simplify((1-t^3)/(1-t))
# β = t^2-t+1
θ = π + atan(t^2-t+1) - atan(t^2+t+1)
diff(θ)
a = solve(diff(θ))
a[1].evalf()
# −0.816496580927726
a[2].evalf()
# 0.816496580927726

数値計算で解を示すなら，二分法かニュートンラフソン法で求解するのが常套手段かな？

Julia でコンソールから入力

コンソールから入力

基本は，

• readline() で文字列を読む。
• 複数のフィールドがあるなら，split(文字列)でフィールドを分ける。
• 分割された文字列を，整数に変換するには parse(Int, 文字列），実数に変換するには parse(Float64, 文字列）。
• 複数の整数，実数変換は parse.() のようにドット記法を使う。
• 変換された要素を配列（ベクトル）に代入，または複数の変数に代入する。

文字列として 1 行入力

入力："abcdefg 12345"

s = readline() # "abcdefg 12345"

区切り文字で区切って複数の文字列として配列（ベクトル）へ入力

デフォルトでは空白区切り

入力："abcdefg 12345"

s = split(readline()) # 要素数 2 のベクトル: "abcdefg", "123"

カンマで区切るとき

入力："123,456,789"

s = split(readline(), ",") # 要素数 3 のベクトル: "123", "456", "789"

複数の変数へ入力

入力："123 456 789"

a, b, c = split(readline()) # 3 変数へ入力: "123", "456", "789"
a # "123"
b # "456"
c # "789"

1 行に整数 1 つ

入力："12345"

n = parse(Int, readline()) # 12345

1 行に実数 1 つ

入力："12345"

f = parse(Float64, readline()) # 12345.0

入力："12.345"

f = parse(Float64, readline()) # 12.345

複数の整数を複数の変数へ入力

入力："12345 67890 11 22"

i, j, k, l = parse.(Int, split(readline())) # i = 12345, j = 67890, k = 11, l = 22

複数の実数を複数の変数へ入力

入力："0.12 4e2 -3.5e-3"

a, b, c = parse.(Float64, split(readline())) # a = 0.12, b = 400.0, c = -0.0035

複数の整数を配列（ベクトル）へ入力

入力："12345 67890 11 22"

n = parse.(Int, split(readline())) # 要素数 4 のベクトル: 12345, 67890, 11, 22

複数の整数を配列（ベクトル）へ入力する（リスト内包表記; 非推奨）

入力："23 45 67"

m = [parse(Int, x) for x in split(readline())] # 23, 45, 67

複数の実数を配列（ベクトル）へ入力

入力："0.12 4e2 -3.5e-3"

f = parse.(Float64, split(readline())) # 要素数 3 のベクトル: 0.12, 400.0, -0.0035

複数の実数を配列（ベクトル）へ入力する（リスト内包表記; 非推奨）

入力："23 45 67"

g = [parse(Float64, x) for x in split(readline())] # 23.0, 45.0, 67.0

読み込む変数の型が複数あるとき（文字列，整数，実数が混ざっているとき）

入力："abc 123 45.67"

a, b, c = split(readline())
a # "abc"
b = parse(Int, b) # 123
c = parse(Float64, c) # 45.67

文字列を入力する（split() しない）と文字に分解されて集合に読み込まれる

入力："qwretudhddhdhshkfh"

s = Set(readline()) # 'f', 'w', 'd', 'e', 'h', 's', 'u', 'r', 't', 'k', 'q'

文字列として集合に読み込ませるには，split() する

入力："abc 123 *&* @@"

s2 = Set(split(readline())) # "abc", "*&*", "@@", "123"

複数行からの入力

1 行に 1 個ずつの整数を n 個（n 行から）入力する

n = 4 # これも入力するなら n = parse(Int, readline())
入力：
"123"
"456"
"789"
"111"

m = [parse(Int, readline()) for s in 1:n] # 123, 456, 789, 111

実数の入力なら parse(Float64, readline()),
文字列そのままを入力するなら readline() のまま

1 行に複数個の整数，別々の配列（ベクトル）の要素として入力

入力：
"1 2 3"
"4 5 6"
"7 8 9"
"0 1 2"

n = 4
a = zeros(Int, n)
b = zeros(Int, n)
c = zeros(Int, n)
for i = 1:n
    a[i], b[i], c[i] = parse.(Int, split(readline()))
end
a # 1, 4, 7, 0
b # 2, 5, 8, 1
c # 3, 6, 9, 2

1 行に複数，入力の都度，処理

n = 5
for i = 1:n
    a, b, c = parse.(Int, split(readline()))
    # a, b, c を使用する処理
end

2 次元配列（行列）へ入力

n x m 行列に読み込む。入力時には m の情報は使わない。1 行当たりの入力個数に注意。

入力：
"1 2 3 4 5"
"6 7 8 9 10"
"11 12 13 14 15"

n, m = 3, 5
A = zeros(Int, n, m)
for i =1:n
    A[i, :] = parse.(Int, split(readline()))
end
A
# 3×5 Array{Int64,2}:
#   1   2   3   4   5
#   6   7   8   9  10
#  11  12  13  14  15

特定の文字列を読むまで繰り返し入力

入力：
"1"
"2"
"3"
"finish"

s = 0
while true
    e = readline()
    e == "finish" && break
    s += parse(Int, e)
end
s # 6

空行が入力されるまで繰り返し入力

入力：
"1"
"2"
"3"
"finish"

s = 0
while true
    try
        e = readline()
        s += parse(Int, e)
    catch
        break
    end
end
s # 6