算額（その1000）

算額（その1000）

一〇五 加須市騎西町中種足 雷神社 大正元年(1912)

埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

正三角形内に楕円，甲円，乙円を入れる。乙円の直径が 1 寸のとき，楕円の短径はいかほどか。

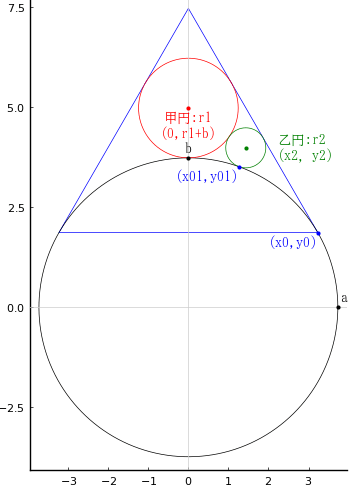
楕円の長半径，短半径，中心座標を a, b, (0, 0)
甲円の半径と中心座標を r1, (0, r1 + b)
乙円の半径と中心座標を r2, (x2, y2)
乙円と楕円の接点座標を (x01, y01)
解が一意であるためには「楕円は正三角形の斜辺と接する」としなければならない。接点の座標を (x0, y0)
とおき，以下の連立方程式を解く。

結果として，楕円は円であり，算額(その571）に帰結する？
https://blog.goo.ne.jp/r-de-r/e/eec3ce5940a63c663911abb152cc382b

include("julia-source.txt");

using SymPy

@syms x0::poitive, y0::poitive, x01::poitive, y01::poitive,
     a::poitive, b::poitive, r1::poitive, r2::poitive,
     x2::poitive, y2
eq1 = x0^2/a^2 + y0^2/b^2 - 1
eq2 = x0/y0 - √Sym(3)
eq3 = -b^2*x0/(a^2*y0) + √Sym(3)
eq4 = x2^2 + (r1 + b - y2)^2 - (r1 + r2)^2
eq5 = (y0 + √Sym(3)*x0 - (r1 + b)) - 2r1
eq6 = dist2(0, y0 + √Sym(3)*x0, x0, y0, x2, y2, r2)
eq7 = x01^2/a^2 + y01^2/b^2 - 1
eq8 = (x2 - x01)^2 + (y2 - y01)^2 - r2^2
eq9 = -b^2*x01/(a^2*y01) + (x2 - x01)/(y2 - y01);

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (x0, y0, x01, y01, a, b, r1, x2, y2) = u
   return [
       -1 + y0^2/b^2 + x0^2/a^2,  # eq1
       x0/y0 - sqrt(3),  # eq2
       sqrt(3) - b^2*x0/(a^2*y0),  # eq3
       x2^2 - (r1 + r2)^2 + (b + r1 - y2)^2,  # eq4
       -b - 3*r1 + sqrt(3)*x0 + y0,  # eq5
       -r2^2 + 3*x0^2/4 - 3*x0*x2/2 + sqrt(3)*x0*y0/2 - sqrt(3)*x0*y2/2 + 3*x2^2/4 - sqrt(3)*x2*y0/2 + sqrt(3)*x2*y2/2 + y0^2/4 - y0*y2/2 + y2^2/4,  # eq6
       -1 + y01^2/b^2 + x01^2/a^2,  # eq7
       -r2^2 + (-x01 + x2)^2 + (-y01 + y2)^2,  # eq8
       (-x01 + x2)/(-y01 + y2) - b^2*x01/(a^2*y01),  # eq9
   ]
end;
r2 = 1/2
iniv = BigFloat[3.2, 1.9, 1.3, 3.5, 3.7, 3.7, 1.2, 1.4, 4]
res = nls(H, ini=iniv)

   ([3.2320508075688767, 1.8660254037844384, 1.2637079407904237, 3.5115873149700736, 3.7320508075688767, 3.7320508075688767, 1.244016935856292, 1.4330127018922192, 3.9820508075688767], true)

長径 = 短径 = 直径 = 3.7320508075688767 の円になる。

その他のパラメータは以下のとおりである。

   短径 = 7.4641;  b = 3.73205;  長径 = 7.4641;  a = 3.73205
   r2 = 0.5;  x0 = 3.23205;  y0 = 1.86603;  x01 = 1.26371;  y01 = 3.51159;  a = 3.73205;  b = 3.73205;  r1 = 1.24402;  x2 = 1.43301;  y2 = 3.98205

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (x0, y0, x01, y01, a, b, r1, x2, y2) = res[1]
   @printf("短径 = %g;  b = %g;  長径 = %g;  a = %g\n", 2b, b, 2a, a)
   @printf("r2 = %g;  x0 = %g;  y0 = %g;  x01 = %g;  y01 = %g;  a = %g;  b = %g;  r1 = %g;  x2 = %g;  y2 = %g\n", r2, x0, y0, x01, y01, a, b, r1, x2, y2)
   plot([x0, 0, -x0, x0], [y0, y0 + √3*x0, y0, y0], color=:blue, lw=0.5)
   ellipse(0, 0, a, b)
   circle(0, r1 + b, r1)
   circle(x2, y2, r2, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r1 + b, "甲円:r1\n(0,r1+b)", :red, :center, delta=-delta/2)
       point(x2, y2, "乙円:r2\n(x2，y2)", :green, :left, :vcenter, deltax=5delta)
       point(x0, y0, "(x0,y0)", :blue, :right, delta=-delta/2)
       point(x01, y01, "(x01,y01)", :blue, :right, delta=-delta/2)
       point(0, b, "b", :black, :center, :bottom, delta=delta/2)
       point(a, 0, "  a", :black, :center, :bottom, delta=delta/2)
   end
end;

算額（その999）

算額（その999）

一〇五 加須市騎西町中種足 雷神社 大正元年(1912)

埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

正方形の中に斜線を 1 本引き，等円を 2 個入れる。等円の直径が 1 寸のとき，正方形の一辺の長さはいかほどか。

正方形の一辺の長さを a
斜線と正方形の一辺上の交点座標を (b, a)
等円の半径と中心座標を r, (r, a - r), (x, r)
とおき，以下の連立方程式を解く。
ただし，r を未知数のまま解くと複雑すぎて SymPy では有限の時間内に解けない。
そこで，r = 1 として解いても，般性を失わない（r が異なる図形は全て相似）。

include("julia-source.txt");

using SymPy

@syms a::poitive, b::poitive, r::poitive, x::poitive
r = 1
eq1 = (x - r)^2 + (a - 2r)^2 - 4r^2
eq2 = dist2(a, 0, b, a, r, a - r, r)/a
eq3 = dist2(a, 0, b, a, x, r, r)/a
res = solve((eq1, eq2, eq3), (a, b, x))
res[9]

   (sqrt(3) + 2, sqrt(3)/3 + 1, 2)

r = 0.5 の場合は，それぞれのパラメータの値は 1/2 になる。
正方形の一辺の長さは (sqrt(3) + 2)/2 = 1.8660254037844386 である。

他に，b = (sqrt(3)/3 + 1)/2 = 0.7886751345948129, x = 1 である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1/2
   (a, b, x) = (sqrt(3) + 2, sqrt(3)/3 + 1, 2) ./ 2
   @printf("r = %g;  a = %g;  b = %g;  x = %g\n", r, a, b, x)
   plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:blue, lw=0.5)
   circle(r, a - r, r)
   circle(x, r, r)
   segment(b, a, a, 0, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r, a - r, "等円:r,(r,a-r)", :red, :center, delta=-delta/2)
       point(x, r, "等円:r,(x,r)", :red, :center, delta=-delta/2)
       point(b, a, "(b,a)", :green, :center, :bottom, delta=delta/2)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
   end
end;

算額（その998）

算額（その998）

一〇五 加須市騎西町中種足 雷神社 大正元年(1912)

埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

外円の中に中心を通る水平な弦（直径）を引き，その上部に 3 個の小円，下部に 1 個の大円を入れる。大円の直径が 1 寸のとき外円の直径はいかほどか。また，小円の直径が 1 寸のとき外円の直径はいかほどか。

対象とする図形は外円の大きさが違っても全て相似なので，外円の直径を 1 としたときの大円，小円の直径を求めれば，それぞれの直径が特定の値を取るときの外円の直径は逆算できる。

外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, r1 - R)
小円の半径と中心座標を r2, (r2, r2, (0, R - r2)
として，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms R::poitive, r1::poitive, r2::poitive
r1 = R/2
eq2 = r2^2 + (R - 2r2)^2 - 4r2^2
res = solve(eq2, r2)[1]  # 1 of 2
res |> println

   R*(2 - sqrt(3))

R = 1/2
r1 = R/2
r2 = R*(2 - sqrt(3))
(2r1, 2r2) |> println

   (0.5, 0.2679491924311228)

外円の直径が 1 の場合，大円の直径は 0.5，小円の直径は 0.2679491924311228 である。
外円の直径 : 大円の直径 : 小円の直径 = 1 : 0.5 : 2 - sqrt(3)

大円の直径が 1 の場合，外円の直径は 1/0.5 = 2 寸
小円の直径が 1 の場合，外円の直径は 1/0.2679491924311228 = 3.732050807568876 寸

1 ./ (0.5, 0.2679491924311228) |> println

   (2.0, 3.732050807568876)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 1/2
   r1 = R/2
   r2 = R*(2 - sqrt(3))
   @printf("外円の直径が %g のとき，大円の直径は %g，小円の直径は %g である。\n", 2R, 2r1, 2r2)
   @printf("大円の直径が 1 のとき，外円の直径は %g である（小円の直径は %g)。\n", 1/2r1, r2/r1)
   @printf("小円の直径が 1 のとき，外円の直径は %g である（大円の直径は %g)。\n", 1/2r2, r1/r2)
   plot()
   circle(0, 0, R)
   circle(0, r1 - R, r1, :magenta)
   circle(0, R - r2, r2, :blue)
   circle2(r2, r2, r2, :blue)
   segment(-R, 0, R, 0, :green, lw=1)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R - r2, "小円:r2,(0,R-r2)", :blue, :center, delta=-delta/2)
       point(r2, r2, "小円:r2,(r2,r2)", :blue, :center, delta=-delta/2)
       point(0, r1 - R, "大円:r1,(0,r1-R)", :magenta, :center, delta=-delta/2)
       point(0, R, "R", :red, :left, :bottom, delta=delta/2)
   end
end;