算額(その994)
一〇一 大宮市高鼻町 氷川神社 明治31年(1898)
埼玉県立図書館:埼玉県史料集 第二集『埼玉の算額』,昭和44年,誠美堂印刷所,埼玉県与野市.

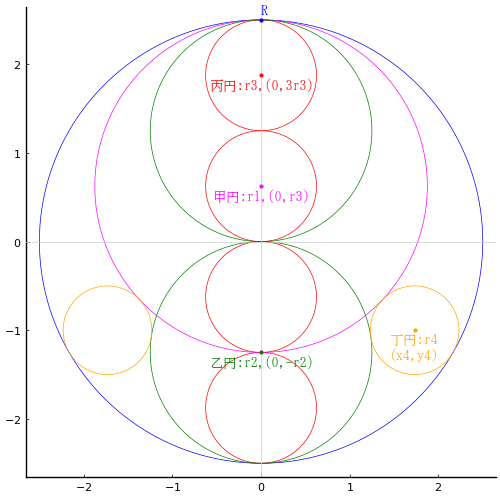
正方形の中に楕円 2 個と,楕円の中に等円をそれぞれ 3 個入れる。等円の直径が 1 寸のとき,正方形の一辺の長さはいかほどか。
正方形の一辺の長さを 2a
等円の半径と中心座標を r, (x, b), (0, 2b - r); b = a/2
とおき,以下の連立方程式を解く。
eq2 は「算法助術」の公式84による。
include("julia-source.txt");
using SymPy
@syms a::poitive, b::positive, r::positive, x::positive
b = a/2
eq1 = x^2 + (2b - r - b)^2 - 4r^2
eq2 = (a^2 - b^2)*(b^2 - r^2)/b^2 - x^2
res = solve([eq1, eq2], (a, x))[1]
(3*r, sqrt(15)*r/2)
楕円の長半径 a は等円の半径 r の 3 倍である。
等円の直径が 1 寸のとき,楕円の長径は 3 寸である。
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = 1/2
(a, x) = (3*r, sqrt(15)*r/2)
b = a/2
@printf("等円の直径が %g のとき,正方形の一辺の長さは %g である。\n", 2r, 2a)
plot([a, a, -a, -a, a], [-a, a, a, -a, -a], color=:green, lw=0.5)
ellipse(0, b, a, b, color=:blue)
ellipse(0, -b, a, b, color=:blue)
circle22(0, 2b - r, r)
circle4(x, b, r)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(a, 0, " a", :green, :left, :bottom, delta=delta/2)
point(0, 2b, " 2b", :green, :left, :bottom, delta=delta/2)
point(x, b, "等円:r,(x,b)", :red, :center, :bottom, delta=delta)
point(0, 2b - r, "等円:r,(0,2b-r)", :red, :center, :bottom, delta=delta)
end
end;