算額（その929）

算額（その929）

群馬県安中市鷺宮 咲前神社 明治20年(1887)
「算額」第三集 全国調査，香川県算額研究会

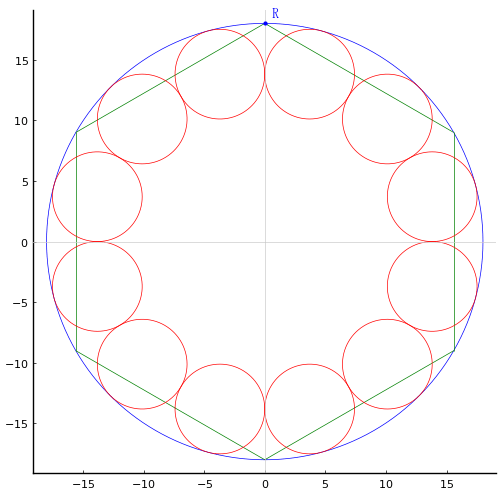
外円の中に大きな菱形が入り，その菱形を合同な 4 個の小さな菱形に区分し，それぞれに内接する等円を入れる。大きな菱形の一辺の長さが 10 寸，等円の直径が 4.8 寸のとき，外円の直径を求めよ。

菱形の一辺の長さを c，短い方の対角線の長さを 2b とする（長いほうの対角線の長さは 2R である）。
菱形の一辺の長さを c とすると，a = sqrt(c^2 - b^2) である。
等円の半径を r とする。中心座標は (0, b/2), (0, -b/2), (R/2, 0), (-R/2, 0) である。
と置き，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms b::positive,
      R::positive, r::positive, x::positive
eq1 = dist2(R, 0, 0, b, R/2, 0, r)
eq2 = R^2 + b^2 - c^2
(R, b) = solve([eq1, eq2], (R, b))[2];  # 2 of 4

R |> println
R(c=>10, r=>2.4) |> println
b |> println
b(c=>10, r=>2.4) |> println

   sqrt(c - sqrt(c^2/2 - c*sqrt(c - 4*r)*sqrt(c + 4*r)/2))*sqrt(c + sqrt(c^2/2 - c*sqrt(c - 4*r)*sqrt(c + 4*r)/2))
   8.00000000000000
   sqrt(c^2/2 - c*sqrt(c - 4*r)*sqrt(c + 4*r)/2)
   6.00000000000000

菱形の一辺の長さが 10 寸，等円の直径が 4.8 寸のとき，外円の直径は 16 寸である。

R と b は，手作業でもう少し簡約化できる。

R |> println

   sqrt(c - sqrt(c^2/2 - c*sqrt(c - 4*r)*sqrt(c + 4*r)/2))*sqrt(c + sqrt(c^2/2 - c*sqrt(c - 4*r)*sqrt(c + 4*r)/2))

R = (√2/2)*sqrt(c^2 + c*sqrt(c^2 - 16r^2))
R(c=>10, r=>2.4) |> println

   8.00000000000000

b |> println

   sqrt(c^2/2 - c*sqrt(c - 4*r)*sqrt(c + 4*r)/2)

b = (√2/2)*sqrt(c^2 - c*sqrt(c^2 - 16*r^2))
b(c=>10, r=>2.4) |> println

   6.00000000000000

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (c, r) = (10, 4.8/2)
   t = c*sqrt(c^2 - 16r^2)
   R = (√2/2)*sqrt(c^2 + t)
   b = (√2/2)*sqrt(c^2 - t)
   @printf("菱形の一辺の長さが　%g，等円の直径が %g のとき，外円の直径は %g である。\n", c, 2r, 2R)
   plot([R, 0, -R, 0, R], [0, b, 0, -b, 0], color=:green, lw=0.5)
   circle(0, 0, R, :blue)
   circle22(0, b/2, r)
   circle2(R/2, 0, r)
   segment(-R/2, -b/2, R/2, b/2, :green)
   segment(R/2, -b/2, -R/2, b/2, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, b, " b", :green, :left, :bottom, delta=delta/2)
       point(R, 0, " R", :green, :left, :bottom, delta=delta/2)
   end
end;

算額（その928）

算額（その928）

群馬県安中市鷺宮 咲前神社 明治20年(1887)
「算額」第三集 全国調査，香川県算額研究会

菱形の中に等円が 12 個入っている。菱形の短い方の対角線が 5.4 寸，菱形の一辺の長さが 4.5 寸のとき，等円の直径はいかほどか。

菱形の長いほうの対角線の長さを 2a，短い方の対角線の長さを 2b とする。
菱形の一辺の長さを c とすると，a = sqrt(c^2 - b^2) である。
等円の半径と中心座標を r, (x, r), (r, y), ((r + x)/2, (r + y)/2)
と置き，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, c::positive,
     r::positive, x::positive, y::positive
a = sqrt(c^2 - b^2) 
eq1 = dist2(a, 0, 0, b, r, y, r)
eq2 = dist2(a, 0, 0, b, x, r, r)
eq3 = (x - r)^2/4 + (y - r)^2/4 - 4r^2 |> expand |> simplify;

eq1, eq2 から y, x を求める。

ans_y = solve(eq1, y)[1]
ans_y |> println
ans_x = solve(eq2, x)[1]
ans_x |> println

   (b^2 - b*c + r*sqrt(-b^2 + c^2))/(b - c)
   (-c*r + (b - r)*sqrt(-b^2 + c^2))/b

y, x を eq3 に代入する。

eq13 = eq3(x => ans_x, y => ans_y) |> expand |> simplify |> numerator
eq13 |> println

   b^3*c^2 - 16*b^3*r^2 - b^2*c^3 - 2*b^2*c^2*r + 16*b^2*c*r^2 + 2*b*c^3*r + 2*b*c^2*r*sqrt(-b^2 + c^2) - 2*c^3*r^2 - 2*c^2*r^2*sqrt(-b^2 + c^2)

r について解く。

ans_r = solve(eq13, r)[2]  # 2 of 2
ans_r |> println

   b*c*(4*b*(b - c) + c*(-b + c + sqrt(-b^2 + c^2)))/(2*(8*b^3 - 8*b^2*c + c^3 + c^2*sqrt(-b^2 + c^2)))

ans_r は b, c のみを含むので，それぞれの値を代入すれば，その条件における等円の直径が求まる。

ans_r(b => 2.7, c=> 4.5) |> println

   0.500000000000001

ans_x, ans_y は b, c の他に r を含む式であるが，上で得られた ans_r を代入すればよい。

ans_x(b => 2.7, c=> 4.5, r => 0.5) |> println
ans_y(b => 2.7, c=> 4.5, r => 0.5) |> println

   2.10000000000000
   1.70000000000000

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (b, c) = (5.4/2, 4.5)
   a = sqrt(c^2 - b^2)
   t = b - c
   r = b*c*(4b*t + c*(a - t))/(2(8b^3 - 8b^2*c + c^3 + c^2*a))
   y = (b^2 - b*c + r*a)/t
   x = (sqrt(-t*(b + c))*(b - r) - c*r)/b
   @printf("a = %g;  b = %g;  c = %g\n", a, b, c)
   @printf("r = %g;  x = %g;  y = %g\n", r, x, y)
   @printf("等円の直径は %g 寸である。\n", 2r)
   plot([a, 0, -a, 0, a], [0, b, 0, -b, 0], color=:green, lw=0.5)
   circle4(r, y, r)
   circle4((r + x)/2, (r + y)/2, r)
   circle4(x, r, r)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r, y, "(r,y)", :red, :right, delta=-delta, deltax=4delta)
       point((r + x)/2, (r + y)/2, "((r+x)/2,(r+y)/2)", :red, :right, delta=-delta, deltax=6delta)
       point(x, r, "(x,r)", :red, :right, delta=-delta, deltax=4delta)
       point(0, b, " b", :green, :left, :bottom, delta=delta/2)
       point(a, 0, " a", :green, :left, :bottom, delta=delta/2)
   end
end;

 

算額（その927）

算額（その927）

群馬県安中市鷺宮 咲前神社 明治20年(1887)
「算額」第三集 全国調査，香川県算額研究会

直角三角形内に大円，小円，等円を入れる。鈎，股がそれぞれ 3 寸，4 寸，大円の直径が 2 寸のとき，等円の直径はいかほどか。

鈎，股，弦を a, b, c
大円の半径と中心座標を r1, (r1, r1)
小円の半径と中心座標を r2, (x2, r2)
等円の半径と中心座標を r3, (x2, r2), (x3, y3)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, c::positive,
     r1::positive, r2::positive, x2::positive,
     r3::positive, x3::positive, y3::positive
# (a, b, r1) = (Sym(3), Sym(4), 2//2)
c = sqrt(a^2 + b^2)
r1 = (a + b - c)//2
r2 = 3r3
eq1 = a*x2 + (b + c)r2 - a*b
eq2 = (x3 - r1)^2 + (r1 - y3)^2 - (r1 - r3)^2 |> expand
eq3 = (x2 - r1)^2 + (r1 - r2)^2 - (r1 + r3)^2 |> expand
eq4 = r2*(b - x3) - y3*(b - x2);
# solve([eq1, eq2, eq3, eq4], (x2, r3, x3, y3))[2]

eq1 を解いて x2 を求める。

ans_x2 = solve(eq1, x2)[1]
ans_x2 |> println

   (a*b - 3*b*r3 - 3*r3*sqrt(a^2 + b^2))/a

eq4 に ans_x2 を代入して y3 を求める。

ans_y3 = solve(eq4(x2 => ans_x2), y3)[1]
ans_y3 |> println

   a*(b - x3)/(b + sqrt(a^2 + b^2))

eq3 に ans_x2 を代入して r3 を求める。

eq13 = eq3(x2 => ans_x2) |> simplify
ans_r3 = solve(eq13, r3)[1] |> simplify
ans_r3 |> println

   a*(7*a^2 + a*b - 7*a*sqrt(a^2 + b^2) - 8*a*sqrt(a^2 - a*sqrt(a^2 + b^2) + b^2) + 6*b^2 + 6*b*sqrt(a^2 + b^2))/(2*(17*a^2 + 18*b^2 + 18*b*sqrt(a^2 + b^2)))

eq2 に ans_y3, ans_x2, ans_r3 を代入して x3 を求める。

eq12 = eq2(y3 => ans_y3, x2 => ans_x2, r3 => ans_r3) |> simplify
ans_x3 = solve(eq12, x3)[2] |> simplify;

ans_x2 = ans_x2(r3 => ans_r3);
ans_y3 = ans_y3(x3 => ans_x3);

x2, x3, y3 は非常に長い式になるが， r3 は程々の長さである。

# ans_x2 |> println
ans_r3 |> println
# ans_x3 |> println
# ans_y3 |> println

   a*(7*a^2 + a*b - 7*a*sqrt(a^2 + b^2) - 8*a*sqrt(a^2 - a*sqrt(a^2 + b^2) + b^2) + 6*b^2 + 6*b*sqrt(a^2 + b^2))/(2*(17*a^2 + 18*b^2 + 18*b*sqrt(a^2 + b^2)))

ans_x2(a => 3, b => 4).evalf() |> println
ans_r3(a => 3, b => 4).evalf() |> println
ans_x3(a => 3, b => 4).evalf() |> println
ans_y3(a => 3, b => 4).evalf() |> println

   2.14429208725912
   0.206189768082320
   1.75307450884191
   0.748975163719364

a, b に特定の値を代入しておけば，自動的に連立方程式を解くことができる。

(x2, r3, x3, y3) =  (77/89 + 36*sqrt(10)/89, 31/89 - 4*sqrt(10)/89, 87*sqrt(10)/445 + 101/89, 85/89 - 29*sqrt(10)/445)

   (2.1442920872591196, 0.20618976808232004, 1.753074508841908, 0.748975163719364

いずれにしろ，鈎 = 3 寸，股 = 4 寸のとき，等円の直径は 2*0.20618976808232004 = 0.41237953616464007 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b) = (3, 4)
   (x2, r3, x3, y3) =  (2.14429208725912, 0.206189768082320, 1.75307450884191, 0.748975163719364)
   c = sqrt(a^2 + b^2)
   r1 = (a + b - c)/2
   r2 = 3r3
   @printf("a = %g;  b = %g;  r1 = %g;  x2 = %g;  r3 = %g;  x3 = %g;  y3 = %g\n", a, b, r1, x2, r3, x3, y3)
   plot([0, b, 0, 0], [0, 0, a, 0], color=:green, lw=0.5)
   circle(r1, r1, r1)
   circle(x2, r2, r2, :blue)
   circle(x2, r2, r3, :magenta)
   circle(x3, y3, r3, :magenta)
   circle(2x2 - x3, 2r2 - y3, r3, :magenta)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1, r1, "大円:r1,(r1,r1)", :red, :center, delta=-delta/2)
       point(x3, y3, "等円:r3,(x3,y3) ", :black, :right, :vcenter)
       point(x2, r2, "小円:r2,(x2,r2)", :black, :left, :bottom, delta=delta, deltax=-3delta)
       point(b, 0, " b", :green, :left, :bottom, delta=delta/2)
       point(0, a, " a", :green, :left, :bottom, delta=delta/2)
   end
end;

算額（その926）

算額（その926）

群馬県安中市鷺宮 咲前神社 明治20年(1887)
「算額」第三集 全国調査，香川県算額研究会

大円に内接する正五角形と，外円に内接すると同時に隣同士外接する 10 個の等円がある。大円の直径が 17 寸のとき，正五角形の一辺の長さと等円の直径を求めよ。

問題を一般化し，正 n 角形を考える。
図は，正六角形の場合で，外円の直径が 36 寸 のとき，正六角形の一辺の長さは 9 寸，等円の直径は 7.40177 寸である。

大円の半径を R，正 n 角形の一辺の長さを p，等円の半径を r とする。

include("julia-source.txt");

using SymPy
@syms R::positive, r::positive, p::positive,
     n::integer

eq_p = R*sind(Sym(180)/n) - p
eq_r = (R - r)sind(Sym(90)/n) - r
p = solve(eq_p, p)[1]
r = solve(eq_r, r)[1]
(p, r)

   (R*sin(pi/n), R*sin(pi/(2*n))/(sin(pi/(2*n)) + 1))

p, r は R と n により決まるので，以下のような関数を定義しておけばよい。
R として大円の直径を与えれば，正 n 角形の一辺の長さと等円の直径を返す。
R として大円の半径を与えれば，正 n 角形の一辺の長さの 1/2 と等円の半径を返す。

func(R, n) = (R*sin(pi/n), R*sin(pi/(2*n))/(sin(pi/(2*n)) + 1));

大円の直径が 17 のとき，正五角形の一辺の長さは 9.992349288972044 寸,等円の直径は 4.013155617496424寸 である。

func(17, 5)

   (9.992349288972044, 4.013155617496424)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, n) = (18, 6)
   (p, r) = func(R, n)
   @printf("外円の直径が %g 寸 のとき，正%i角形の一辺の長さは %g 寸，等円の直径は %g 寸である。\n", 2R, n, p, 2r)
   plot()
   circle(0, 0, R, :blue)
   θ = range(90, 450, length=n + 1)
   x = @. R*cosd(θ)
   y = @. R*sind(θ)
   for i in 1:n
       segment(x[i], y[i], x[i + 1], y[i + 1], :green)
   end
   rotate((R - r)*cosd(90 + 90/n), (R - r)*sind(90 + 90/n), r, angle=180/n)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, " R", :blue, :left, :bottom, delta=delta/2)
   end
end;

算額（その925）

算額（その925）

群馬県安中市鷺宮 咲前神社 明治20年(1887)
「算額」第三集 全国調査，香川県算額研究会

外円の中に大円と小円を 2 個ずつ入れる。外円，大円の直径がそれぞれ 16 寸，6 寸 のとき，小円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (r1, y1)
小円の半径と中心座標を r2, (0, R - 3r2), (0, R - r2)
とおき，以下の連立方程式を解く。

単なる二元連立方程式なのに，一般解を求めようとしても，SymPy では有限の時間内で解くことはできないようである。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, y1::negative,
     r2::positive
@syms R, r1, y1, r2
eq1 = r1^2 + y1^2 - (R - r1)^2 |> expand
eq2 = r1^2 + (R - 3r2 - y1)^2 - (r1 + r2)^2 |> expand

まず eq1 を解き，y1 を求める。

ans_y1 = solve(eq1, y1)[1]
ans_y1 |> println
ans_y1(R => 16/2, r1 => 6/2) |> println

   -sqrt(R*(R - 2*r1))
   -4.00000000000000

次に，eq2 に y1 を代入し，r を求める。

eq12 = eq2(y1 => ans_y1) |> simplify
eq12 |> println

   2*R^2 - 2*R*r1 - 6*R*r2 + 2*R*sqrt(R*(R - 2*r1)) - 2*r1*r2 + 8*r2^2 - 6*r2*sqrt(R*(R - 2*r1))

ans_r2 = solve(eq12, r2)[1]  # 1 of 2
ans_r2 |> println
ans_r2(R => 16/2, r1 => 6/2) |> println
2*ans_r2(R => 16/2, r1 => 6/2) |> println

   3*R/8 + r1/8 + 3*sqrt(R*(R - 2*r1))/8 - sqrt(2*R^2 + 4*R*r1 + 2*R*sqrt(R*(R - 2*r1)) + r1^2 + 6*r1*sqrt(R*(R - 2*r1)))/8
   2.47382841096268
   4.94765682192536

外円，大円の直径がそれぞれ 16 寸，6 寸 のとき，小円の直径は 4.94765682192536 である。

同類項を含むので，以下のようにして簡潔に計算できる。
   t = sqrt(R^2 - 2R*r1)
   r2 = (3R + r1 + 3t - sqrt(2R^2 + 4R*r1 + 2R*t + r1^2 + 6r1*t))/8
   y1 = -t

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, r1) = (16, 6) .// 2
   t = sqrt(R^2 - 2R*r1)
   r2 = (3R + r1 + 3t - sqrt(2R^2 + 4R*r1 + 2R*t + r1^2 + 6r1*t))/8
   y1 = -t
   @printf("外円の直径が %g 寸，大円の直径が %g 寸のとき，小円の直径は %g 寸である。\n", 2R, 2r1, 2r2)
   plot()
   circle(0, 0, R, :blue)
   circle(0, R - r2, r2)
   circle(0, R - 3r2, r2)
   circle2(r1, y1, r1, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R - 3r2, "小円:r2,(0,R-3r2)", :red, :center, delta=-delta/2)
       point(r1, y1, "大円:r1,(r1,y1)", :green, :center, delta=-delta/2)
       point(0, R, " R", :blue, :left, :bottom, delta=delta/2)

   end
end;