算額（その943）

算額（その943）

宮城県大崎市岩出（旧岩出山町; 注） 八幡神社 大正3年()
「算額」第四集 全国調査，香川県算額研究会

注：現大崎市岩出には大崎八幡神社，古館八幡神社，鍋倉山八幡神社，八幡神社がある。

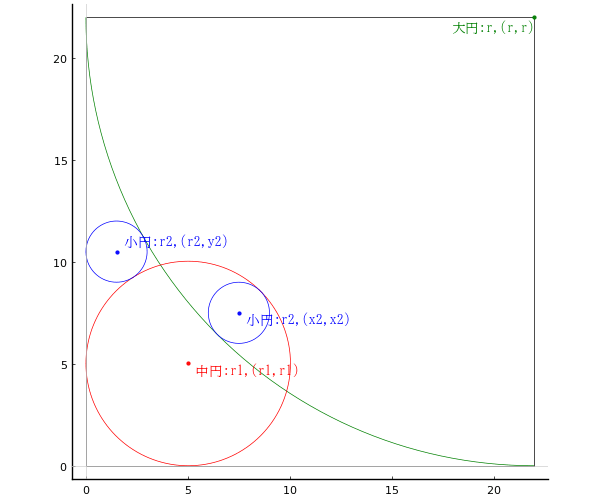
楕円内に菱形，その中に大円 2 個，小円 2 個が入っている。楕円の長径，短径，大円の直径を与えたとき，小円の直径を求めよ。

算額（その669）の菱形の外接楕円をお飾りで余分に加えたものである。
もともとの「問」では，楕円の長径，短径，大円の直径の 3　条件が与えられることになっているが，それでは条件が過剰である。長径，短径を与えて大円，小円の直径を求めよという問題にしなければならない。

楕円の長半径，短半径を a, b
大円の半径と中心座標を r1, (0, r1)
小円の半径と中心座標を r2, (x2, r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

@syms a::positive, b::positive, r1::positive,
     r2::positive, x2::positive, c
c = sqrt(a^2 + b^2)  # コメントのままにしておくこと
eq1 = r1/(b - r1) - a/c
eq2 = r2/(a - x2) - b/c
eq3 = r1^2 + x2^2 - (r1 + r2)^2
res = solve([eq1, eq2, eq3], (r1, r2, x2))[1]  # 1 of 2

   (a*b/(a + c), a*b*(-a*c - b^2 + b*sqrt(a^2 + 4*a*c + b^2 + 3*c^2) - c^2)/(a*b^2 - a*c^2 + b^2*c - c^3), a*b*(a*b + 2*b*c - c*sqrt(a^2 + 4*a*c + b^2 + 3*c^2))/(a*b^2 - a*c^2 + b^2*c - c^3))

大円の半径は短い式で表すことができるが，小円の半径径の式は長い。
楕円の長径，短径が 288, 84 (a = 144, b = 42) のとき，小円の直径 2r2 は 56.0 である。

a = 288/2
b = 84/2
c = sqrt(a^2 + b^2)
a*b*(-a*c - b^2 + b*sqrt(a^2 + 4*a*c + b^2 + 3*c^2) - c^2)/(a*b^2 - a*c^2 + b^2*c - c^3)

   28.0

その他のパラメータは以下のとおりである。

   a = 144;  b = 42;  r1 = 20.5714;  r2 = 28;  x2 = 44

function draw(more=false)
   pyplot(size=(600, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b) = (288, 84) ./ 2
   c = sqrt(a^2 + b^2)
   s = sqrt(a^2 + 4*a*c + b^2 + 3*c^2)
   t = a*b^2 - a*c^2 + b^2*c - c^3
   (r1, r2, x2) = (
       a*b/(a + c),
       a*b*(-a*c - b^2 + b*s - c^2)/t,
       a*b*(a*b + 2*b*c - c*s)/t)
   @printf("a = %g;  b = %g;  r1 = %g;  r2 = %g;  x2 = %g\n", a, b, r1, r2, x2)
   plot([a, 0, -a, 0, a], [0, b, 0, -b, 0], color=:black, lw=0.5)
   ellipse(0, 0, a, b, color=:magenta)
   circle22(0, r1, r1)
   circle2(x2, 0, r2, :blue)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :magenta, :left, :bottom, delta=delta/2)
       point(0, b, " b", :magenta, :left, :bottom, delta=delta/2)
       point(0, r1, "大円:r1,(0,r1)", :red, :center, delta=-delta/2)
       point(x2, 0, "小円:r2,(x2,r2)", :blue, :center, delta=-delta/2)
   end
end;

算額（その942）

算額（その942）

福島県南会津郡南会津町塩江宮ノ下（旧田島町水田） 鷲神社 文久元年(1861)
「算額」第四集 全国調査，香川県算額研究会

直線上に 2 個の大円があり，その間に正方形が挟まっている。
正方形の一辺の長さが 1 寸のとき，大円の直径はいかほどか。

正方形の一辺の長さを 2a
大円の半径と中心座標を r1, (r1, r1)
とおき，以下の方程式を解く。

include("julia-source.txt");

@syms a::positive, r1::positive
eq = (a - r1)^2 + (2a - r1)^2 - r1^2
eq |>  println

   -r1^2 + (a - r1)^2 + (2*a - r1)^2

eq |> factor |> println

   (-5*a + r1)*(-a + r1)

(-5*a + r1)*(-a + r1) = 0 を解くわけであるが，a ≠ r1 なので，5a = r1 の関係である。
正方形の一辺の長さが 1 寸ならば 5/2 = r1 で，大円の直径は 5 寸とわかるし，
大円の直径が 5　寸ならば 5a = 2.5 で，正方形の一辺の長さが 1 寸とわかる。

function draw(more=false)
   pyplot(size=(600, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 1/2
   r1 = 5/2
   plot()
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(0, 2a, " 2a", :blue, :left, :bottom, delta=delta/2)
       point(r1, r1, "(r1, r1)", :red, :center, :bottom, delta=delta)
   end
   circle2(r1, r1, r1)
   rect(-a, 0, a, 2a, :blue)
   segment(-2r1, 0, 2r1, 0, :green, lw=1)
end;

算額（その941）

算額（その941）

山形市小白川町 天満神社（天満宮） 明治14年(1881)
「算額」第四集 全国調査，香川県算額研究会

正方形の中に，大円（四分円），中円，小円を入れる。正方形の一辺の長さが与えられたとき，小円の直径を求めよ。

正方形の一辺の長さ（大円の半径）を r
中円の半径と中心座標を r1, (r1, r1)
小円の半径と中心座標を r2, (x2, x2), (r2, y2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

@syms r::positive, r1::positive,
     r2::positive, x2::positive, y2::positive
eq1 = 2(x2 - r1)^2 - (r1 - r2)^2
eq2 = (r - r2)^2 + (r - y2)^2 - (r + r2)^2
eq3 = (r1 -r2)^2 + (y2 - r1)^2 - (r1 + r2)^2
eq4 = 2(r - x2)^2 - (r - r2)^2
res = solve([eq1, eq2, eq3, eq4], (r1, r2, x2, y2))[3]  # 3 of 4

   (r*(113 - 72*sqrt(2))/49, r*(9 - 4*sqrt(2))/49, 5*r*(9 - 4*sqrt(2))/49, r*(9 - 4*sqrt(2))/7)

小円の半径 r2 は，正方形の一辺の長さ r の (9 - 4√2)/49 倍である。
正方形の一辺の長さ r が 22 寸のとき，小円の直径 2r2 は 3.00201 寸である。

2 * 22 * (9 - 4√2)/49

   3.00200842902725

その他のパラメータは以下のとおりである。

r = 22;  r1 = 5.01808;  r2 = 1.501;  x2 = 7.50502;  y2 = 10.507

function draw(more=false)
   pyplot(size=(600, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 22
   (r1, r2, x2, y2) = r .* ((113 - 72√2)/49, (9 - 4√2)/49, 5(9 - 4√2)/49, (9 - 4√2)/7)
   @printf("正方形の一辺の長さ = %g;  中円の直径 = %g;  小円の直径 = %g\n", r, 2r1, 2r2)
   @printf("r = %g;  r1 = %g;  r2 = %g;  x2 = %g;  y2 = %g\n", r, r1, r2, x2, y2)
   plot([0, r, r, 0, 0], [0, 0, r, r, 0], color=:black, lw=0.5)
   circle(r, r, r, :green, beginangle=180, endangle=270)
   circle(r1, r1, r1)
   circle(r2, y2, r2, :blue)
   circle(x2, x2, r2, :blue)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1, r1, " 中円:r1,(r1,r1)", :red)
       point(x2, x2, " 小円:r2,(x2,x2)", :blue)
       point(r2, y2, " 小円:r2,(r2,y2)", :blue, :left, :bottom, delta=delta/2)
       point(r, r, "大円:r,(r,r)", :green, :right, delta=-delta/2)
   end
end;