算額（その910）

算額（その910）

一一三 熊谷市熊谷 大神宮 昭和辛丑（昭和36年，1961年）

埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

楕円内に等円 2 個，小円 1 個を入れる。小円の直径が与えられたとき，楕円の長径，短径を求めよ。

楕円の長半径，短半径，中心座標を a, b, (0, 0)
等円の半径と中心座標を r1, (a - r1, 0)
小円の半径と中心座標を r2, (0, b - r2)
とおき，以下の連立方程式を解く。

なお，等円も小円も曲率円である。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, r1::positive,
     r2::positive
eq1 = r1 - b^2/a
eq2 = a - 2r1
eq3 = (a - r1)^2 + (b - r2)^2 - (r1 + r2)^2
res = solve([eq1, eq2, eq3], (a, b, r1))[1]

   (2*r2*(1 + sqrt(2)), r2*(sqrt(2) + 2), r2*(1 + sqrt(2)))

楕円の長半径は小円の半径の 2 + 2√2 倍，楕円の短半径は小円の半径の 2 + √2 倍である。
小円の直径が 1 のとき，楕円の長径，短径はそれぞれ 4.82842712474619, 3.414213562373095 である。
ちなみに，等円の直径は 2.414213562373095 である。

その他のパラメータは以下のとおりである。
r2 = 0.5;  a = 2.41421;  b = 1.70711;  r1 = 1.20711

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (a, b, r1) = r2 .* (2 + 2√2, 2 + √2, 1 + √2)
   @printf("楕円の長径 = %g，楕円の短径 = %g\n", 2a, 2b)
   @printf("r2 = %g;  a = %g;  b = %g;  r1 = %g\n", r2, a, b, r1)
   plot()
   ellipse(0, 0, a, b, color=:red)
   circle2(a - r1, 0, r1, :blue)
   circle22(0, b - r2, r2, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :red, :left, :bottom, delta=delta/2)
       point(0, b, " b", :red, :left, :bottom, delta=delta/2)
       point(a - r1, 0, "等円:r1\n(a-r1,0)", :blue, :center, delta=-2delta)
       point(0, b - r2, "小円:r2\n(0,b-r2)", :green, :center, delta=-2delta)
   end
end;

算額（その909）

算額（その909）

一一三 熊谷市熊谷 大神宮 昭和辛丑（昭和36年，1961年）

埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

楕円の中に大円 1 個，等円（曲率円である） 2 個が入っている。等円の直径を与えたとき，楕円の長径，短径を求めよ。

楕円の長半径，短半径，中心座標を a, b, (0, 0)
大円の半径と中心座標を r1, (0, 0); r1 = b
等円の半径と中心座標を r2, (a - r2, 0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, r1::positive,
     r2::positive
r1 = b
eq1 = r2 - b^2/a
eq2 = r1 + 2r2 - a
res = solve([eq1, eq2], (a, b))[1]

   (4*r2, 2*r2)

楕円の長半径 a，短半径 b は，等円（曲率円）の半径の 4 倍と 2 倍である。
等円（曲率円）の直径が 1 のとき，楕円の長径は 4，短径は 2 である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (a, b) = r2 .* (4, 2)
   r1 = b
   @printf("等円の直径 = %g，楕円の長径 = %g，楕円の短径 = %g\n", 2r2, 2a, 2b)
   @printf("r2 = %g;  a = %g;  b = r1 = %g\n", r2, a, b)
   plot()
   ellipse(0, 0, a, b, color=:red)
   circle2(a - r2, 0, r2, :blue)
   circle(0, 0, r1, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :red, :left, :bottom, delta=delta/2)
       point(0, b, " b=r1", :red, :left, :bottom, delta=delta/2)
       point(0, 0, "大円:r1\n(0,0)", :green, :center, delta=-2delta)
       point(a - r2, 0, "等円:r2\n(0,a-r2)", :blue, :center, delta=-2delta)
   end
end;

算額（その908）

算額（その908）

一〇〇 桶川市小針領家 氷川諏訪神社 明治30年(1897)

埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

全円内に甲円 5 個，乙円 5 個，丙円 4 個が入っている。甲円の直径が 1 寸 2 分 5 厘のとき，丙円の直径はいかほどか。

全円の半径と中心座標を R, (0, 0); R = 2r1 + r2
甲円の半径と中心座標を r1, (r1, r1), (0, 0)
乙円の半径と中心座標を r2, (0, R - r2), (0, 0)
丙円の半径と中心座標を r3, (x3, x3); x3 = (r2 + r3)/√2
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive,
     r3::positive, x3::positive, y3::negative
eq1 = r1 - r2 - 2r3
eq2 = 2r1 + r2 - R
eq3 = (r2 + r3)/√Sym(2) - x3
eq4 = r1^2 + (R - r2 - r1)^2 - (r1 + r2)^2;
res = solve([eq1, eq2, eq3, eq4], (R, r2, r3, x3))[1]

   (r1*(1 + sqrt(2)), r1*(-1 + sqrt(2)), r1*(2 - sqrt(2))/2, r1/2)

丙円の半径は甲円の半径の 1 - √2/2 倍である。
甲円の直径が 1 寸 2 分 5 厘のとき，丙円の直径は 0.36611652351681556 寸である。

その他のパラメータは以下のとおりである。

r1 = 0.625;  R = 1.50888;  r2 = 0.258883;  r3 = 0.183058;  x3 = 0.3125

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1.25/2
   (R, r2, r3, x3) = r1 .* (1 + √2, √2 - 1, 1 - √2/2, 1/2)
   @printf("甲円の直径 = %g，丙円の直径 = %g\n", 2r1, 2r3)
   @printf("r1 = %g;  R = %g;  r2 = %g;  r3 = %g;  x3 = %g\n", r1, R, r2, r3, x3)
   (R, r2, r3, x3) = (r1*(1 + sqrt(2)), r1*(-1 + sqrt(2)), r1*(2 - sqrt(2))/2, r1/2)
   plot()
   circle(0, 0, R, :green)
   circle(0, 0, r1)
   circle4(r1, r1, r1)
   circle(0, 0, r2, :blue)
   circle4(x3, x3, r3, :magenta)
   circle42(0, R - r2, r2, :blue)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, " R", :green, :left, :bottom, delta=delta/2)
       point(r1, r1, "甲円:r1\n(r1,r1)", :red, :left, :vcenter, deltax=delta)
       point(0, R - r2, "乙円:r2,(0,R-r2)", :black, :center, :bottom, delta=delta/2)
       point(x3, x3, "丙円:r3,(x3,x3)", :black, :center, :bottom, delta=delta/2, deltax=5delta)
       point(r2, 0, "r2 ", :blue, :right, delta=-delta/2)
       point(r1, 0, " r1", :red, :left, delta=-delta/2)
   end
end;

算額（その907）

算額（その907）

一〇〇 桶川市小針領家 氷川諏訪神社 明治30年(1897)

埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

正方形の中に甲円 1 個，乙円 2 個を入れる。正方形の一辺の長さが 2 寸 5 分，乙円の直径が 7 分のとき，甲円の直径はいかほどか。

正方形の一辺の長さと頂点座標を a，(a/√2，0), (0, a/√2), (-a/√2, 0), (0, -a/√2)
甲円の半径と中心座標を r1, (0, y1)
乙円の半径と中心座標を r2, (r2, y2); y2 < 0
とおき，以下の連立方程式を立てる。

include("julia-source.txt");

using SymPy
@syms a::positive, a2::positive, r1::positive,
     y1::positive, r2::positive, y2::negative
a2 = a/√Sym(2)
eq1 = r2^2 + (y1 - y2)^2 - (r1 + r2)^2
eq2 = dist2(a2, 0, 0, a2, 0, y1, r1)
eq3 = dist2(a2, 0, 0, -a2, r2, y2, r2);
eq1 |> println
eq2 |> println
eq3 |> println

   r2^2 - (r1 + r2)^2 + (y1 - y2)^2
   a^2/4 - sqrt(2)*a*y1/2 - r1^2 + y1^2/2
   a^2/4 - sqrt(2)*a*r2/2 + sqrt(2)*a*y2/2 - r2^2/2 - r2*y2 + y2^2/2

SymPy の性能上，一度に解くことができないので，逐次解いてゆく。
まず eq2 を解き，y1 を求める

ans_y1 = solve(eq2, y1)[1]
ans_y1 |> println

   sqrt(2)*(a/2 - r1)

eq1, eq3 に代入する。

eq11 = eq1(y1 => ans_y1) |> expand
eq11 |> println
eq13 = eq3(y1 => ans_y1) |> expand
eq13 |> println

   a^2/2 - 2*a*r1 - sqrt(2)*a*y2 + r1^2 - 2*r1*r2 + 2*sqrt(2)*r1*y2 + y2^2
   a^2/4 - sqrt(2)*a*r2/2 + sqrt(2)*a*y2/2 - r2^2/2 - r2*y2 + y2^2/2

eq13 を解き，y2 を求める。この式は a, r2 だけを含むので y2 は決定される。

ans_y2 = solve(eq13, y2)[1]
ans_y2 |> println

   -sqrt(2)*a/2 + r2 + sqrt(2)*r2

eq11 に y1, y2 を代入する。

eq21 = eq11(y1 => ans_y1, y2 => ans_y2) |> simplify
eq21 |> println

   2*a^2 - 4*a*r1 - 4*a*r2 - 2*sqrt(2)*a*r2 + r1^2 + 2*r1*r2 + 2*sqrt(2)*r1*r2 + 2*sqrt(2)*r2^2 + 3*r2^2

eq21 は a, r2 だけを含むので r1 は決定される。

ans_r1 = solve(eq21, r1)[1]
ans_r1 |> println

   -sqrt(2)*sqrt(a)*sqrt(a - sqrt(2)*r2) + 2*a - sqrt(2)*r2 - r2

r1 が決まれば，逆順にたどり，y1 が決定される。

r2 = 0.7/2 # 半径を与える
a = 2.5
r1 = -sqrt(2)*sqrt(a)*sqrt(a - sqrt(2)*r2) + 2*a - sqrt(2)*r2 - r2
y2 = -sqrt(2)*a/2 + r2 + sqrt(2)*r2
y1 = sqrt(2)*(a/2 - r1)
(r1, y1, y2)
# (0.9887772739600998, 0.3694247219656983, -0.9227922061357855)

   (0.9887772739600998, 0.3694247219656983, -0.9227922061357855)

甲円の直径は 2(2a - (1 + √2)r2 -√2sqrt(a^2 - √2r2*a))
正方形の一辺の長さ a が 2 寸 5 分，乙円の直径 r2 が 7 分のとき，甲円の直径は 1.9775545479202004 寸である。

r2 = 0.7/2 # 半径を与える
a = 2.5
2(2a - (1 + √2)r2 -√2sqrt(a^2 - √2r2*a))

   1.9775545479202004

その他のパラメータは以下のとおりである。
a = 2.5;  r2 = 0.35;  r1 = 0.988777;  y1 = 0.369425;  y2 = -0.922792

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 0.7/2
   a = 2.5
   r1 = -sqrt(2)*sqrt(a)*sqrt(a - sqrt(2)*r2) + 2*a - sqrt(2)*r2 - r2
   y2 = -sqrt(2)*a/2 + r2 + sqrt(2)*r2
   y1 = sqrt(2)*(a/2 - r1)
   a2 = a/√2
   @printf("正方形の一辺の長さ = %g，乙円の直径 = %g のとき，甲円の直径は %g である。\n", a, 2r2, 2r1)
   @printf("a = %g;  r2 = %g;  r1 = %g;  y1 = %g;  y2 = %g\n", a, r2, r1, y1, y2)
   plot([a2, 0, -a2, 0, a2], [0, a2, 0, -a2, 0], color=:blue, lw=0.5, xlims=(-2, 2.2))
   circle(0, y1, r1, :green)
   circle2(r2, y2, r2)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, a/√2, " a/√2", :blue, :left, :bottom, delta=delta/2)
       point(a/√2, 0, " a/√2", :blue, :left, :bottom, delta=delta/2)
       point(0, y1, "甲円:r1,(0,y1)", :green, :center, delta=-delta/2)
       point(r2, y2, "乙円:r2\n(r2,y2)", :red, :center, delta=-delta/2)
   end
end;

算額（その906）

算額（その906）

一〇〇 桶川市小針領家 氷川諏訪神社 明治30年(1897)

埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

甲円，乙円，丙円と「三角面」がある。甲円，丙円の直径がそれぞれ 2.7 寸，0.6 寸のとき，乙円の直径を求めよ。

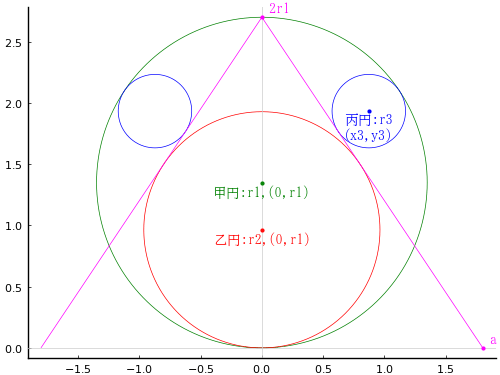
注：「問」では「三角面」とあるが，通常「三角面」は「正三角形」を表す。しかし，この問題では「三角形」は正三角形ではなく「二等辺三角形」である。

三角形の底辺の長さを 2a
甲円の半径と中心座標を r1, (0, r1)
乙円の半径と中心座標を r2, (0, r2)
丙円の半径と中心座標を r3, (x3, y3)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, r1::positive, r2::positive,
     r3::positive, x3::positive, y3::positive

#(r1, r3) = (27, 6) .// 2
eq1 = r2/(2r1 - r2) - a/sqrt(4r1^2 + a^2)
eq2 = x3^2 + (y3 - r1)^2 - (r1 - r3)^2
eq3 = x3/(y3 - r1) - 2r1/a
eq4 = dist2(a, 0, 0, 2r1, x3, y3, r3)
res = solve([eq1, eq2, eq3, eq4], (r2, a, x3, y3))

   1-element Vector{NTuple{4, Sym{PyCall.PyObject}}}:
    (2*r1*(r1 - 2*r3)*sqrt(r1^3 - 3*r1^2*r3 + 3*r1*r3^2 - r3^3)/(r1^3*sqrt((r1^3 - 3*r1^2*r3 + 3*r1*r3^2 - r3^3)/(r1^4 - 4*r1^3*r3 + 6*r1^2*r3^2 - 4*r1*r3^3 + r3^4)) - 2*r1^2*r3*sqrt((r1^3 - 3*r1^2*r3 + 3*r1*r3^2 - r3^3)/(r1^4 - 4*r1^3*r3 + 6*r1^2*r3^2 - 4*r1*r3^3 + r3^4)) + r1*r3^2*sqrt((r1^3 - 3*r1^2*r3 + 3*r1*r3^2 - r3^3)/(r1^4 - 4*r1^3*r3 + 6*r1^2*r3^2 - 4*r1*r3^3 + r3^4)) + r1*sqrt(r1^3 - 3*r1^2*r3 + 3*r1*r3^2 - r3^3) - 2*r3*sqrt(r1^3 - 3*r1^2*r3 + 3*r1*r3^2 - r3^3)), r1*(r1 - 2*r3)*sqrt(r1^3 - 3*r1^2*r3 + 3*r1*r3^2 - r3^3)/(sqrt(r3)*(r1^2 - 2*r1*r3 + r3^2)), 2*sqrt(r3)*sqrt((r1 - r3)^3)/r1, 2*r1 - 3*r3 + 2*r3^2/r1)

r2 の式は長く複雑なものである。
しかし，術は見事に簡約化された解である。
d1 = 2r1, d3 = 2r3 として，
d1^2 - 2d1*d3)/(d1 - d3)

r2 の簡約化を手動で行おう。

sqrt() の中の長い式は (r1 - r3)^3 と (r1 - r3)^4 に因数分解できる。

r1^3 - 3*r1^2*r3 + 3*r1*r3^2 - r3^3 |> factor |> println
r1^4 - 4*r1^3*r3 + 6*r1^2*r3^2 - 4*r1*r3^3 + r3^4 |> factor |> println

   (r1 - r3)^3
   (r1 - r3)^4

(r1 - r3) を t とおいて簡約化する。

@syms t::positive, d
R2= res[1][1](r1^3 - 3*r1^2*r3 + 3*r1*r3^2 - r3^3 => t^3, r1^4 - 4*r1^3*r3 + 6*r1^2*r3^2 - 4*r1*r3^3 + r3^4 => t^4)
R2 = apart(R2, d) |> simplify
R2 |> println

   2*r1*t^2*(r1 - 2*r3)/(r1^3 - 2*r1^2*r3 + r1*r3^2 + r1*t^2 - 2*r3*t^2)

ここで，t をもとの (r1 - r3) に戻す。

R3 = R2(t => (r1 - r3))
R3 |> println

   2*r1*(r1 - 2*r3)*(r1 - r3)^2/(r1^3 - 2*r1^2*r3 + r1*r3^2 + r1*(r1 - r3)^2 - 2*r3*(r1 - r3)^2)

長くなったように見えるが simplify すると術で述べられているのと同じ式になる。

R4 = R3 |> simplify
R4 |> println

   r1*(r1 - 2*r3)/(r1 - r3)

R4(r1 => 2.7/2, r3 => 0.6/2).evalf() * 2 |> println

   1.92857142857143

甲円，丙円の直径がそれぞれ 2.7 寸，0.6 寸のとき，乙円の直径は 1.92857142857143 寸である。

当たり前のことであるが，この式に直径を与えると，答えも直径で得られる。

R4(r1 => 2.7, r3 => 0.6) |> println

   1.92857142857143

その他のパラメータは以下のとおりである。

r2 = 0.964286;  a = 1.80401;  x3 = 0.873053;  y3 = 1.93333

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r3) = (2.7, 0.6) ./ 2
   (r2, a, x3, y3) = (
       r1*(r1 - 2*r3)/(r1 - r3),
       r1*(r1 - 2*r3)*sqrt((r1 - r3)^3)/(sqrt(r3)*(r1 - r3)^2),
       2*sqrt(r3)*sqrt((r1 - r3)^3)/r1,
       2*r1 - 3*r3 + 2*r3^2/r1
   )
   @printf("乙円の直径 = %g\n", 2r2)
   @printf("r2 = %g;  a = %g;  x3 = %g;  y3 = %g\n", r2, a, x3, y3)
   plot()
   circle(0, r1, r1, :green)
   circle(0, r2, r2)
   circle(x3, y3, r3, :blue)
   segment(0, 2r1, a, 0, :magenta)
   segment(0, 2r1, -a, 0, :magenta)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r1, "甲円:r1,(0,r1)", :green, :center, delta=-delta/2)
       point(0, r2, "乙円:r2,(0,r1)", :red, :center, delta=-delta/2)
       point(x3, y3, "丙円:r3\n(x3,y3)", :blue, :center, delta=-delta/2)
       point(a, 0, " a", :magenta, :left, :bottom, delta=delta/2)
       point(0, 2r1, " 2r1", :magenta, :left, :bottom, delta=delta/2)
   end
end;