算額（その934）

算額（その934）

栃木県真岡市東郷（注） 大前神社 絵馬堂 紀元2536年（明治9年(1876)）
「算額」第三集 全国調査，香川県算額研究会

注： 住所は，真岡市荒井町となっていたが，現在は真岡市東郷か。

交差する大円の中に 6 個の小円を入れる。小円の直径が与えられたときに，大円の直径を求めよ。

大円の半径と中心座標を r1, (x1, 0), (-x1, 0)
小円の半径と中心座標を r2, (x2, r2); x2 = 2x1
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms r1::positive, x1::positive, r2::positive, x2::positive
x1 = x2/2
eq1 = x1^2 + r2^2 - (r1 - r2)^2
eq2 = (x1 + x2)^2 + r2^2 - (r1 + r2)^2
res = solve([eq1, eq2], (r1, x2))[1]
res |> println

   (5*r2/2, sqrt(5)*r2)

大円の半径は小円の半径の 5/2 倍である。
小円の直径が 1 寸のとき，大円の直径は 2.5 寸である。

その他のパラメータは以下のとおりである。

r2 = 0.5;  r1 = 1.25;  x2 = 1.11803;  x1 = 0.559017

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (r1, x2) = (5*r2/2, sqrt(5)*r2)
   x1 = x2/2
   @printf("小円の直径が %g 寸のとき，大円の直径は %g 寸である。\n", 2r2, 2r1)
   @printf("r2 = %g;  r1 = %g;  x2 = %g;  x1 = %g\n", r2, r1, x2, x1)
   plot()
   circle2(x1, 0, r1, :blue)
   circle4(x2, r2, r2)
   circle22(0, r2, r2)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x1, 0, "大円:r1,(x1,0)", :blue, :left, delta=-delta/2)
       point(-x1, 0, "", :blue)
       point(x2, r2, "小円:r2,(x2,r2)", :red, :center, delta=-delta/2)
   end
end;

算額（その933）

算額（その933）

群馬県安中市下磯部 磯部神社 天保7年(1830)
「算額」第三集 全国調査，香川県算額研究会

大正方形内に円と 3 個の小正方形とを入れる。大正方形の一辺の長さが 1 寸のとき，円の直径はいかほどか。

大正方形の一辺の長さを 2a
小正方形の一辺の長さを b
円の半径を r
とおく。
連立方程式を解くほどのものでもないが，以下のようにして r, b を求める。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, r::positive
eq1 = a - (1 + √Sym(3))b/2
eq2 = (a - b) - 2r
res = solve([eq1, eq2], (r, b))
res |> println

   Dict{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}(b => 2*a/(1 + sqrt(3)), r => -a/(2 + 2*sqrt(3)) + sqrt(3)*a/(2 + 2*sqrt(3)))

res[r](a => 1/2).evalf() |> println
res[b](a => 1/2).evalf() |> println

   0.0669872981077807
   0.366025403784439

大正方形の一辺の長さが 1 寸のとき，円の直径は 0.133975 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 1/2
   b = 2a/(1 + √3)
   r = (2a - a - b)/2
   @printf("大正方形の一辺の長さが %g 寸のとき，円の直径は %g 寸\n", 2a, 2r)
   @printf("a = %g;  r = %g;  b = %g\n", a, r, b)
   plot(a.*[1, 1, -1, -1, 1], 2a.*[0, 1, 1, 0, 0], color=:green, lw=0.5)
   circle(0, 2a - r, r, :blue)
   rect(-b/2, 2a - 2r - b, b/2, 2a - 2r, :magenta)
   plot!(b.*[0, √3/2, (√3 + 1)/2, 1/2, 0], b.*[1/2, 0, √3/2, (1 + √3)/2, 1/2], color=:magenta, lw=0.5)
   plot!(-b.*[0, √3/2, (√3 + 1)/2, 1/2, 0], b.*[1/2, 0, √3/2, (1 + √3)/2, 1/2], color=:magenta, lw=0.5)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 2a - r, " 円:r,(0,2a-r)", :black, :left, :vcenter)
       point(b/2, 2a-2r-b, " (b/2,2a-2r-b)", :magenta, :left, :bottom, delta=delta/2)
       point(0, b/2, " b/2", :magenta, :left, :bottom, delta=-delta/2)
       point(b√3/2, 0, "  b√3/2", :magenta, :left, :bottom, delta=delta/2)
       point(a, 0, " a", :green, :left, :bottom, delta=delta/2)
       point(0, 2a, " 2a", :green, :left, :bottom, delta=delta/2)
   end
end;

算額（その932）

算額（その932）

群馬県安中市下磯部 磯部神社 天保7年(1830)
「算額」第三集 全国調査，香川県算額研究会

直角三角形内に大円 1 個，小円 3 個が入っている。大円の直径が与えられたとき，小円の直径を求めよ。

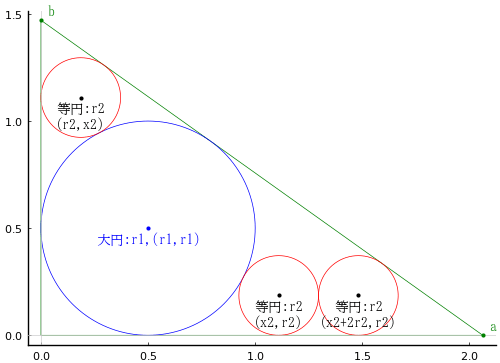
直角三角形の直角を挟む 2 辺の長さを a, b; b > a
大円の半径と中心座標を r1, (r1, r1)
小円の半径と中心座標を r2, (x2, r2), (x2 + 2r2, r2), (r2, x2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, c::positive,
     r1::positive, r2::positive, x2::positive
c = sqrt(a^2 + b^2)
eq1 = a + b - c - 2r1
eq2 = (r1 - r2)^2 + (x2 - r1)^2 - (r1 + r2)^2
eq3 = dist2(a, 0, 0, b, r2, x2, r2);
eq4 = dist2(a, 0, 0, b, x2 + 2r2, r2, r2);

println(eq1, ",  # eq1")
println(eq2, ",  # eq2")
println(eq3, ",  # eq3")
println(eq4, ",  # eq4") 

   a + b - 2*r1 - sqrt(a^2 + b^2),  # eq1
   (-r1 + x2)^2 + (r1 - r2)^2 - (r1 + r2)^2,  # eq2
   a^2*b^2 - 2*a^2*b*x2 - a^2*r2^2 + a^2*x2^2 - 2*a*b^2*r2 + 2*a*b*r2*x2,  # eq3
   a^2*b^2 - 2*a^2*b*r2 - 4*a*b^2*r2 - 2*a*b^2*x2 + 4*a*b*r2^2 + 2*a*b*r2*x2 + 3*b^2*r2^2 + 4*b^2*r2*x2 + b^2*x2^2,  # eq4

ans_a = solve(eq1, a)[1] 
ans_a |> println

   2*r1*(b - r1)/(b - 2*r1)

eq3 = eq3(a => ans_a) |> simplify |> numerator |> (x -> x/(4r1*(b - r1)))
eq3 |> println

   b*r2*(-b + x2)*(b - 2*r1) + r1*(b - r1)*(b^2 - 2*b*x2 - r2^2 + x2^2)

eq4 = eq4(a => ans_a)|> simplify |> numerator |> (x -> x/b) |> simplify
eq4 |> println

   b*(b - 2*r1)^2*(3*r2^2 + 4*r2*x2 + x2^2) + 4*r1^2*(b - r1)^2*(b - 2*r2) - 4*r1*(b - 2*r1)*(b - r1)*(2*b*r2 + b*x2 - 2*r2^2 - r2*x2)

ans_b = solve(eq3, b)[1]
ans_b |> println

   (-r1*r2 + r1*x2)/(r1 - r2)

eq4 = eq4(b => ans_b) |> simplify |> numerator |> (x -> x/r1^3);
eq4 |> println

   4*r1*(r1 - x2)^2*(-r1*r2 + r1*x2 - 2*r2*(r1 - r2)) + 4*(r1 - x2)*(2*r1 - r2 - x2)*(2*r1*r2*(r2 - x2) + r1*x2*(r2 - x2) + r2*(r1 - r2)*(2*r2 + x2)) - (r2 - x2)*(2*r1 - r2 - x2)^2*(3*r2^2 + 4*r2*x2 + x2^2)

ans_x2 = solve(eq2, x2)[2]
ans_x2 |>  println

   2*sqrt(r1)*sqrt(r2) + r1

eq4 = eq4(x2 => ans_x2) |> simplify
eq4 |> println

   10*r1^(9/2)*sqrt(r2) - 32*r1^(7/2)*r2^(3/2) + 4*r1^(5/2)*r2^(5/2) + 80*r1^(3/2)*r2^(7/2) - 30*sqrt(r1)*r2^(9/2) + r1^5 + 25*r1^4*r2 - 158*r1^3*r2^2 + 218*r1^2*r2^3 - 51*r1*r2^4 - 3*r2^5

ans_r2 = solve(eq4, r2)[1]  # 1 of 3
ans_r2 |> println

   r1*CRootOf(x^3 - 55*x^2 + 23*x - 1, 1)

CRootOf(x^3 - 55*x^2 + 23*x - 1, 1) は x^3 - 55*x^2 + 23*x - 1 = 0 の複素数解の 1 番目のものという意味で，数式では表せないが，数値としては 0.371791858437119 である。

大円の半径 r1 が 4247 のとき，小円の半径 r2 は 0.371791858437119*r1 = 1579.00002278245 である。

ans_r2.evalf() |> println
ans_r2(r1 => 8494/2).evalf() |> println

   0.371791858437119*r1
   1579.00002278245

sympy.CRootOf() を使わないで解くと以下のようになる。虚数解の虚数部は誤差範囲で 0 である。

@syms x
eq = x^3 - 55*x^2 + 23*x - 1;

solve(eq)[1].evalf() |> println

   0.371791858437119 - 0.e-21*I

すべてのパラメータは以下のとおりである。

r1 = 4247
r2 = 0.371791858437119*r1
x2 = 2*sqrt(r1)*sqrt(r2) + r1
b = (-r1*r2 + r1*x2)/(r1 - r2)
a = 2*r1*(b - r1)/(b - 2*r1)
(a, b, r2, x2)

   (17518.388377740157, 12491.392010408297, 1579.0000227824444, 9426.19418317446)

大円の直径が 8494 寸のとき，等円の直径は 2*1579.0000227824444 = 3158.0000455648888 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1/2
   r2 = 0.371791858437119*r1
   x2 = 2*sqrt(r1)*sqrt(r2) + r1
   b = (-r1*r2 + r1*x2)/(r1 - r2)
   a = 2*r1*(b - r1)/(b - 2*r1)
   @printf("大円の直径が %.10g 寸のとき，等円の直径は %.10g 寸である。\n", 2r1, 2r2)
   @printf("r1 = %g;  r2 = %g;  x2 = %g;  a = %g;  b = %g\n", r1, r2, x2, a, b)
   plot([0, a, 0, 0], [0, 0, b, 0], color=:green, lw=0.5)
   circle(r1, r1, r1, :blue)
   circle(r2, x2, r2)
   circle(x2, r2, r2)
   circle(x2 + 2r2, r2, r2)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :green, :left, :bottom, delta=delta/2)
       point(0, b, " b", :green, :left, :bottom, delta=delta/2)
       point(r1, r1, "大円:r1,(r1,r1)", :blue, :center, delta=-delta)
       point(r2, x2, "等円:r2\n(r2,x2)", :black, :center, delta=-delta)
       point(x2, r2, "等円:r2\n(x2,r2)", :black, :center, delta=-delta)
       point(x2 + 2r2, r2, "等円:r2\n(x2+2r2,r2)", :black, :center, delta=-delta)
   end
end;

算額（その931）

算額（その931）

群馬県安中市下磯部 磯部神社 天保7年(1830)
「算額」第三集 全国調査，香川県算額研究会

台形内に大円，小円，等円が入っている。大円の直径が 10 寸のとき，等円の直径はいかほどか。

横倒しになっているが，台形の高さ，下底，上底の長さを a, b, c
大円の半径と中心座標を r1, (r1, r1)
小円の半径と中心座標を r2, (a - r2, r2)
等円の半径と中心座標を r3, (r3, y31), (x3, r3)
とおき，以下の連立方程式の数値解を求める。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, c::positive,
     r1::positive, r2::positive, r3::positive,
     x3::positive, y31::positive, y32::positive
eq1 = (r1 - r3)^2 + (y31 - r1)^2 - (r1 + r3)^2
eq2 = (x3 - r1)^2 + (y32 - r1)^2 - (r1 + r3)^2
eq3 = (a - r2 - r1)^2 + (r1 - r2)^2 - (r1 + r2)^2
eq4 = (a - r2 - x3)^2 + (y32 - r2)^2 - (r2 + r3)^2
eq5 = dist2(a, c, 0, b, r3, y31, r3)
eq6 = dist2(a, c, 0, b, x3, y32, r3)
eq7 = dist2(a, c, 0, b, r1, r1, r1)
eq8 = dist2(a, c, 0, b, a - r2, r2, r2);

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (a, b, c, r2, r3, x3, y31, y32) = u
   return [
       (-r1 + y31)^2 + (r1 - r3)^2 - (r1 + r3)^2,  # eq1
       (-r1 + x3)^2 + (-r1 + y32)^2 - (r1 + r3)^2,  # eq2
       (r1 - r2)^2 - (r1 + r2)^2 + (a - r1 - r2)^2,  # eq3
       (-r2 + y32)^2 - (r2 + r3)^2 + (a - r2 - x3)^2,  # eq4
       a^2*b^2 - 2*a^2*b*y31 - a^2*r3^2 + a^2*y31^2 - 2*a*b^2*r3 + 2*a*b*c*r3 + 2*a*b*r3*y31 - 2*a*c*r3*y31,  # eq5
       a^2*b^2 - 2*a^2*b*y32 - a^2*r3^2 + a^2*y32^2 - 2*a*b^2*x3 + 2*a*b*c*x3 + 2*a*b*x3*y32 - 2*a*c*x3*y32 - b^2*r3^2 + b^2*x3^2 + 2*b*c*r3^2 - 2*b*c*x3^2 - c^2*r3^2 + c^2*x3^2,  # eq6
       a^2*b^2 - 2*a^2*b*r1 - 2*a*b^2*r1 + 2*a*b*c*r1 + 2*a*b*r1^2 - 2*a*c*r1^2,  # eq7
       a^2*c^2 - 2*a^2*c*r2 + 2*a*b*c*r2 - 2*a*b*r2^2 - 2*a*c^2*r2 + 2*a*c*r2^2,  # eq8
   ]
end;
r1 = 10/2
iniv = BigFloat[18, 11, 7, 4, 1, 10, 10, 8]
res = nls(H, ini=iniv)

   ([18.121162012570196, 11.12823119917143, 7.415656960521699, 4.083745164389245, 1.1267889889060243, 10.427965642765756, 9.747186511832085, 7.841607343658628], true)

大円の直径が 10 寸のとき，等円の直径は 2*1.1267889889060243 = 2.2535779778120486 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 10/2
   (a, b, c, r2, r3, x3, y31, y32) = res[1]
   println("2r3 = $(2r3)")
   plot([0, a, a, 0,  0], [0, 0, c, b, 0], color=:green, lw=0.5)
   circle(r1, r1, r1, :blue)
   circle(a - r2, r2, r2, :green)
   circle(r3, y31, r3, :magenta)
   circle(x3, y32, r3, :magenta)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :green, :left, :bottom, delta=delta/2)
       point(a, c, "(a,c)", :green, :left, :bottom, delta=2delta, deltax=-7delta)
       point(0, b, " b", :green, :left, :bottom, delta=delta/2)
       point(r1, r1, "大円:r1,(r1,r1)", :blue, :center, delta=-2delta)
       point(a - r2, r2, "小円:r2,(a-r2,r2)", :green, :center, delta=-2delta)
       point(r3, y31, "等円:r3\n(r3,y31)", :black, :left, delta=-2delta, deltax=-5delta)
       point(x3, y32, "等円:r3\n(x3,y32)", :black, :left, delta=-2delta, deltax=-5delta)
   end
end;

算額（その930）

算額（その930）

群馬県安中市下磯部 磯部神社 天保7年(1830)
「算額」第三集 全国調査，香川県算額研究会

円と正方形が横に並んで外接している。円の中心から正方形の遠い方の頂点までの距離が 15 寸，正方形の一辺の長さが 10 寸のとき，円の直径はいかほどか。

正方形の一辺の長さを a
円の半径を r
円の中心と正方形の頂点までの距離を d
とおき，以下の方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, r::positive, d::positive
eq1 = (r + a)^2 + (a - r)^2 - d^2
r = solve(eq1, r)[1]
r |> println

   sqrt(-4*a^2 + 2*d^2)/2

2r(a => 10, d => 15) |> println
2r(a => 10, d => 15).evalf() |> println

   5*sqrt(2)
   7.07106781186548

正方形の一辺の長さが 10，円の中心から正方形の頂点までの距離が 15 のとき，円の直径は 7.07106781186548 である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, d) = (10, 15)
   r = sqrt(-4a^2 + 2d^2)/2
   @printf("正方形の一辺の長さが %g，円の中心から頂点までの距離が %g のとき，円の直径は %g である。\n", a, d, 2r)
   plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:green, lw=0.5)
   circle(-r, r, r, :blue)
   segment(-r, r, a, a, :red)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       #vline!([0], color=:black, lw=0.5)
       plot!(showaxis=false)
   end
end;