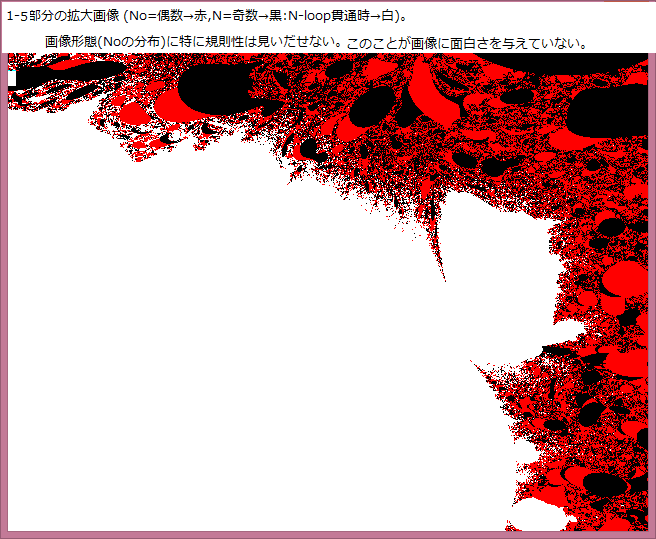
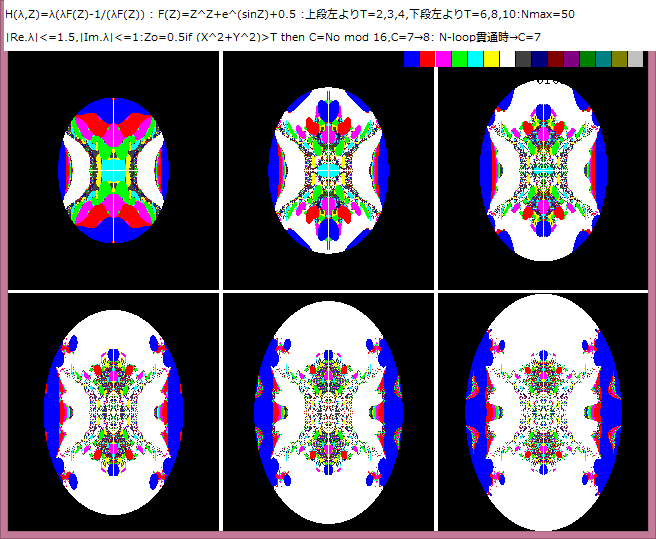
力学系:微分方程式の振る舞いの追跡について。
(参考文献)『コンピューター・カオス・フラクタル』(C.A.ピックオーバー著、白揚社))
次式のサイクル系に関する離散時間位相平面を考える。
dX(t)/dt=-f(Y(t)) ・・・(1)
dY(t)/dt=-f(X(t)) ・・・(2)
ここで関数:fは周波数変調で使われる次式を考える。
f(x)=sin(x+sin(ρx)) ・・・(3)
(3)式をコンビューターで扱うために次式のオイラー近似を使用する。
X(t+1)-X(t)=-hf(Y(t)) ・・・(4)
Y(t+1)-Y(t)=hf(X(t)) ・・・(5)
ここで、hは小さい値とする。
今、X(t)を横軸、Y(t)を縦軸とする位相平面を考え、t が 離散的に変化したときの式(4)(5)で決定される点(X(t),Y(t))の軌跡を表示させる。
***
ここで、この軌跡を求める実際のBASIC/98のプログラムにおいて以下の
パラメータを用いる。
(a)表示する横軸=XS~XE :480ピクセル
(b)表示する縦軸=YS~YE :480ピクセル
(c)tの変化:T=0→TMAX (step 1)
(d)X(t)及びY(t)の倍率=L (但し、画像の中心点は固定する)
(e)初期値の与え方は以下のようにする。
横軸:XS~XE、及び縦軸:YS~YEをD等分する。
即ち、DX=(XE-XS)/D:DY=(YE-YS)/Dとする。
ここで、初期値:x(0)=XX,y(0)=YYを以下のように変化させる。
FOR JJ=0 TO D
YY=YS+DY*JJ
FOR KK=0 TO D
XX=XS+DX*KK
NEXT KK
NEXT JJ
***
上記の(e)でのJJ,KK ループにおいて、点(X(T),Y(T)を N=0→NMAXで求めて表示させれば、微分方程式(1)(2)の t の変化による挙動軌跡が求まる。
***
f(x)=sin{x+sin(3x)},XS=-20,XE=20,YS=-20,YE=20,D=500,L=1,TMAX=500
の場合のBASIC/98のプログラムの具体例を下記に示す。
但し、上記の参考文献では具体的プログラムが書かれていないため、以下のプログラムは私の独自のものである。パラメーターの具体的与え方は恐らく参考文献とは異なることを注意しておく。
10 REM 力学系
20 REM parameter→行140
30 REM 横軸(K):480 dots、縦軸(J):480 dots
80 COLOR 0,7,,,2
90 CLS 3
140 XS=-20:XE=20:YS=-20:YE=20:H=0.1:D=500:L=1:TMAX=500
150 DX=(XE-XS)/D:DY=(YE-YS)/D
180 FOR JJ=0 TO D
200 YY=YS+DY*JJ :Y1=YY
210 FOR KK=0 TO D
211 XX=XS+DX*KK
220 FOR T=0 TO TMAX
221 X=XX:Y=YY
230 XX=X-H*SIN(Y+SIN(3*Y))
240 YY=Y+H*SIN(X+SIN(3*X))
241 XXX=L*XX:YYY=L*YY
250 J=12*YYY+240
260 K=12*XXX+240
270 IF J<0 OR J>480 THEN 310
280 IF K<0 OR K>480 THEN 310
290 PSET (K,J),0
310 NEXT T
314 YY=Y1
320 NEXT KK
330 NEXT JJ
340 END
***
次記事より具体的画像を求める。
(参考文献)『コンピューター・カオス・フラクタル』(C.A.ピックオーバー著、白揚社))
次式のサイクル系に関する離散時間位相平面を考える。
dX(t)/dt=-f(Y(t)) ・・・(1)
dY(t)/dt=-f(X(t)) ・・・(2)
ここで関数:fは周波数変調で使われる次式を考える。
f(x)=sin(x+sin(ρx)) ・・・(3)
(3)式をコンビューターで扱うために次式のオイラー近似を使用する。
X(t+1)-X(t)=-hf(Y(t)) ・・・(4)
Y(t+1)-Y(t)=hf(X(t)) ・・・(5)
ここで、hは小さい値とする。
今、X(t)を横軸、Y(t)を縦軸とする位相平面を考え、t が 離散的に変化したときの式(4)(5)で決定される点(X(t),Y(t))の軌跡を表示させる。
***
ここで、この軌跡を求める実際のBASIC/98のプログラムにおいて以下の
パラメータを用いる。
(a)表示する横軸=XS~XE :480ピクセル
(b)表示する縦軸=YS~YE :480ピクセル
(c)tの変化:T=0→TMAX (step 1)
(d)X(t)及びY(t)の倍率=L (但し、画像の中心点は固定する)
(e)初期値の与え方は以下のようにする。
横軸:XS~XE、及び縦軸:YS~YEをD等分する。
即ち、DX=(XE-XS)/D:DY=(YE-YS)/Dとする。
ここで、初期値:x(0)=XX,y(0)=YYを以下のように変化させる。
FOR JJ=0 TO D
YY=YS+DY*JJ
FOR KK=0 TO D
XX=XS+DX*KK
NEXT KK
NEXT JJ
***
上記の(e)でのJJ,KK ループにおいて、点(X(T),Y(T)を N=0→NMAXで求めて表示させれば、微分方程式(1)(2)の t の変化による挙動軌跡が求まる。
***
f(x)=sin{x+sin(3x)},XS=-20,XE=20,YS=-20,YE=20,D=500,L=1,TMAX=500
の場合のBASIC/98のプログラムの具体例を下記に示す。
但し、上記の参考文献では具体的プログラムが書かれていないため、以下のプログラムは私の独自のものである。パラメーターの具体的与え方は恐らく参考文献とは異なることを注意しておく。
10 REM 力学系
20 REM parameter→行140
30 REM 横軸(K):480 dots、縦軸(J):480 dots
80 COLOR 0,7,,,2
90 CLS 3
140 XS=-20:XE=20:YS=-20:YE=20:H=0.1:D=500:L=1:TMAX=500
150 DX=(XE-XS)/D:DY=(YE-YS)/D
180 FOR JJ=0 TO D
200 YY=YS+DY*JJ :Y1=YY
210 FOR KK=0 TO D
211 XX=XS+DX*KK
220 FOR T=0 TO TMAX
221 X=XX:Y=YY
230 XX=X-H*SIN(Y+SIN(3*Y))
240 YY=Y+H*SIN(X+SIN(3*X))
241 XXX=L*XX:YYY=L*YY
250 J=12*YYY+240
260 K=12*XXX+240
270 IF J<0 OR J>480 THEN 310
280 IF K<0 OR K>480 THEN 310
290 PSET (K,J),0
310 NEXT T
314 YY=Y1
320 NEXT KK
330 NEXT JJ
340 END
***
次記事より具体的画像を求める。