巡回符号 (2)

sys.pdf sys-s.pdf sys.txt 記事一覧

[4-17] 4を法とする積

#41: 有限体

符号理論の参考書をみると，多項式環，ガロア拡大体等，多くの用語が使われています．伝統的な説明では「群」→「環」→「体」の順に代数的構造を発展させますが，ここでは [4-17] と同様に（群には言及しないで）剰余類から始めます．

整数 x を 3 で割った剰余 x mod 3 を f(x) で表わすと，f(x)∈{0, 1, 2} です．また f(x)，f(y)の和，積を

   f(x) ＋ f(y) ＝ f(x + y)，   f(x)・f(y) ＝ f(x y)

で定義すると加法，乗法の結合法則，交換法則および分配法則が成立し，f(0)＝0，f(1)＝1 が加法，乗法の単位元になっています．さらに，任意の x について

   f(x) ＋ Y ＝ 0，   f(x)・Z ＝ 1

となる {0, 1, 2} の元 Y，Z が存在します．例えば  f(5)＋1＝2＋1＝0， f(5)・2＝2・2＝1 です． したがって整数 x を 3 で割った剰余の集合に対する四則演算が可能，つまり ({0, 1, 2}, ＋, ・) は体になっています．

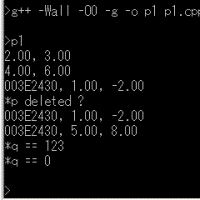
しかし，整数 x を 4 で割った剰余の場合は，上図のように x y ≠ 0 でも f(x)・f(y) ＝ 0 となることがあります（体になっていない）．多項式の因数分解

   X² ＋ 3・X ＋ 2 ＝ (X ＋ 1)・(X ＋ 2)

も「 X² ＋ 3・X ＋ 2 ＝ 0 」が 「 X ＋ 1 ＝ 0 または X ＋ 2 ＝ 0 」と同値でなければ（体になっていなければ）ほとんど使い物になりません．単純に和，積を

   f(x) ＋ f(y) ＝ f(x + y)，   f(x)・f(y) ＝ f(x y)

で定義しても体になるのは素数で割った剰余の場合だけですが，幸いなことに集合の要素の数が一つの素数のべき乗に等しければ，和，積を適当に定義することにより体にできます．

[4-8] 有限体 - Wikipedia
  http://ja.wikipedia.org/wiki/%E6%9C%89%E9%99%90%E4%BD%93
[4-9] 体 (数学) - Wikipedia
  http://ja.wikipedia.org/wiki/%E4%BD%93_(%E6%95%B0%E5%AD%A6)
[4-10] 代数的構造 - Wikipedia
  http://ja.wikipedia.org/wiki/%E4%BB%A3%E6%95%B0%E7%9A%84%E6%A7%8B%E9%80%A0
[4-11] 標数 - Wikipedia
  http://ja.wikipedia.org/wiki/%E6%A8%99%E6%95%B0
  有限体 F の位数が素数 p の冪 p^f ならば、F の標数は p である。
  逆に、標数 p の有限体の位数は必ず p の冪になる。
[4-12] 剰余類環 - Wikipedia
  http://ja.wikipedia.org/wiki/%E5%89%B0%E4%BD%99%E9%A1%9E%E7%92%B0
[4-13] 合同式 - Wikipedia
  http://ja.wikipedia.org/wiki/%E5%90%88%E5%90%8C%E5%BC%8F
[4-14] 準同型 - Wikipedia
  http://ja.wikipedia.org/wiki/%E6%BA%96%E5%90%8C%E5%9E%8B
[4-15] 核 (数学) - Wikipedia
  http://ja.wikipedia.org/wiki/%E6%A0%B8_(%E6%95%B0%E5%AD%A6)
  余像 Coim(h) は h の像 Im(h) = h(S) と同型であるという命題を準同型定理という。
[4-16] 環・体(群、環、体)
  http://ufcpp.net/study/group/field.html#finite
[4-17] 有限体 - 手抜きLab＠DTPの現場
  http://chuwa.iobb.net/tech/archive/2009/05/post-1.html
  ウィキを見てみたのだけど、余計に分からなくなる罠だったわけだね。
  で、ここからが本番となるんだ。ガロア拡大体というものの説明がひつようになるんだ。
[4-18] 代数学 - [物理のかぎしっぽ]
  http://hooktail.org/misc/index.php?%C2%E5%BF%F4%B3%D8
  ※ 時間に余裕のある人はこちらの各資料をご覧下さい．