| sys.pdf sys-s.pdf 記事一覧 |
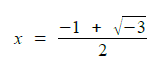 代数的整数 x |
GB7%1:GF(3)の拡大 (1)
武部幹先生のゼミに関連して,整数論の入り口部分を復習しました.
GF(2)上の生成多項式で構成される巡回符号では多項式の係数が 0,1 しかなく有理数体上の多項式で体を拡大するときの話を想像し難いので,巡回符号の基礎知識を前提として sys-s.pdf 用の資料
http://www18.ocn.ne.jp/~pulsar/tmp/sys-E2S.pdf
を作りましたが,割愛した事項が多いのでブログで補足事項を連載します.
1.整数とは?
高校の数学でも,『方程式 x2 + 1 = 0 は実数解をもたないが,i2 + 1 = 0 を満足する数 i が存在すると仮定して』 i を含む多項式の四則演算を行い,i2 に -1 を代入して整理した a + b i の形の式を求めました.例えば
(1 + 2 i)(3 + 4 i)(5 + 6 i) = (-5 + 10 i)(5 + 6 i) = 35 + 20 i
です.実数を係数とする多項式を
P(x) = Q(x)(x2 + 1) + a x + b
のように書き換えて,x に i を代入すると,P(i) = a i + b が得られます.P(x) = 0 となる実数が存在しないとき,P(x) は(実数体上での)既約多項式であるといいます.「実数とは何か」という問題は難しいので,以下では有理数で考えます.方程式 x2 - 2 = 0 は有理数の解を持ちませんが, α2 - 2 = 0 である数α(= 21/2 )が存在するとしてαを含む多項式を計算し,α2 に 2 を代入して整理すると a α + b の形になります.
一般に,代数的数(有理係数の多項式の根となる複素数)のうち,最高次の係数が1であって他の係数がすべて有理整数 (高校で学ぶ有理数体に属する整数) である多項式の根となる数を代数的整数 (数学者がいう整数) といいます.したがって,方程式が x2 + 3 = 0 の根である
x = (-1 + (-3)1/2)/2
も(代数的)整数です.有理数体を3次の方程式 x3 - 2 = 0 の根で拡大して得られる体の元は a 22/3 + b 21/3 + c の形になり,この体もさらに別の方程式 y2 + 1 = 0 の根で拡大できます.
関連資料([n]は本文でも引用, *.pptはブロック解除が面倒なので未調査):
[0] 応用代数学入門―暗号・符号・バーコードの仕組みが分かる: D. W. ハーディ, C. L. ウォーカー
http://www.amazon.co.jp/%E5%BF%9C%E7%94%A8%E4%BB%A3%E6%95%B0%E5%AD%A6%E5%85%A5%E9%96%80%E2%80%95%E6%9A%97%E5%8F%B7%E3%83%BB%E7%AC%A6%E5%8F%B7%E3%83%BB%E3%83%90%E3%83%BC%E3%82%B3%E3%83%BC%E3%83%89%E3%81%AE%E4%BB%95%E7%B5%84%E3%81%BF%E3%81%8C%E5%88%86%E3%81%8B%E3%82%8B-%E3%83%80%E3%83%AC%E3%83%AB%E3%83%BBW-%E3%83%8F%E3%83%BC%E3%83%87%E3%82%A3/dp/4894714930
--------
[1] ガロア理論の頂を踏む (BERET SCIENCE): 石井 俊全
http://www.amazon.co.jp/%E3%82%AC%E3%83%AD%E3%82%A2%E7%90%86%E8%AB%96%E3%81%AE%E9%A0%82%E3%82%92%E8%B8%8F%E3%82%80-BERET-SCIENCE-%E7%9F%B3%E4%BA%95-%E4%BF%8A%E5%85%A8/dp/4860643631
[2] 代数と数論の基礎 (共立講座 21世紀の数学): 中島 匠一
http://www.amazon.co.jp/%E4%BB%A3%E6%95%B0%E3%81%A8%E6%95%B0%E8%AB%96%E3%81%AE%E5%9F%BA%E7%A4%8E-%E5%85%B1%E7%AB%8B%E8%AC%9B%E5%BA%A7-21%E4%B8%96%E7%B4%80%E3%81%AE%E6%95%B0%E5%AD%A6-%E4%B8%AD%E5%B3%B6-%E5%8C%A0%E4%B8%80/dp/4320015614/ref=pd_sim_b_1?ie=UTF8&refRID=0M8GK4SJ5EPYM6D95HCY
[3] 代数方程式とガロア理論 (共立叢書 現代数学の潮流): 中島 匠一
http://www.amazon.co.jp/%E4%BB%A3%E6%95%B0%E6%96%B9%E7%A8%8B%E5%BC%8F%E3%81%A8%E3%82%AC%E3%83%AD%E3%82%A2%E7%90%86%E8%AB%96-%E5%85%B1%E7%AB%8B%E5%8F%A2%E6%9B%B8-%E7%8F%BE%E4%BB%A3%E6%95%B0%E5%AD%A6%E3%81%AE%E6%BD%AE%E6%B5%81-%E4%B8%AD%E5%B3%B6-%E5%8C%A0%E4%B8%80/dp/4320016963
[4] 整数論 (基礎数学講座): 稲葉栄次
http://www.amazon.co.jp/%E6%95%B4%E6%95%B0%E8%AB%96-%E5%9F%BA%E7%A4%8E%E6%95%B0%E5%AD%A6%E8%AC%9B%E5%BA%A7-%E7%A8%B2%E8%91%89%E6%A0%84%E6%AC%A1/dp/432001359X
※ 手元にあるのは数十年前に購入したこれだけです.他の資料は一部の図書館での閲覧,Webでの立ち読み等.
[5] 初等整数論講義 第2版: 高木 貞治
http://www.amazon.co.jp/%E5%88%9D%E7%AD%89%E6%95%B4%E6%95%B0%E8%AB%96%E8%AC%9B%E7%BE%A9-%E7%AC%AC2%E7%89%88-%E9%AB%98%E6%9C%A8-%E8%B2%9E%E6%B2%BB/dp/4320010019
[6] 代数的整数論 第2版: 高木 貞治
http://www.amazon.co.jp/%E4%BB%A3%E6%95%B0%E7%9A%84%E6%95%B4%E6%95%B0%E8%AB%96-%E7%AC%AC2%E7%89%88-%E9%AB%98%E6%9C%A8-%E8%B2%9E%E6%B2%BB/dp/4000056301
--------
[7] 体の拡大 - Wikipedia
http://ja.wikipedia.org/wiki/%E4%BD%93%E3%81%AE%E6%8B%A1%E5%A4%A7
[8] 有限体 - Wikipedia
http://ja.wikipedia.org/wiki/%E6%9C%89%E9%99%90%E4%BD%93
[9] 剰余環 - Wikipedia
http://ja.wikipedia.org/wiki/%E5%89%B0%E4%BD%99%E7%92%B0










※コメント投稿者のブログIDはブログ作成者のみに通知されます